Ce tutoriel est un guide convivial pour les débutants apprendre les structures de données et les algorithmes en utilisant Python. Dans cet article, nous aborderons les structures de données intégrées telles que les listes, les tuples, les dictionnaires, etc., ainsi que certaines structures de données définies par l'utilisateur telles que listes chaînées , des arbres , graphiques , etc., et des algorithmes de traversée ainsi que de recherche et de tri à l'aide d'exemples bons et bien expliqués et de questions pratiques.

Listes

Listes Python sont des collections ordonnées de données, tout comme les tableaux dans d'autres langages de programmation. Il autorise différents types d’éléments dans la liste. L'implémentation de Python List est similaire à Vectors en C++ ou ArrayList en JAVA. L'opération coûteuse consiste à insérer ou à supprimer l'élément depuis le début de la liste car tous les éléments doivent être déplacés. L'insertion et la suppression en fin de liste peuvent également devenir coûteuses dans le cas où la mémoire pré-allouée devient pleine.

alphabet en chiffres

Exemple : création d'une liste Python

List = [1, 2, 3, 'GFG', 2.3] print(List)>

[1, 2, 3, 'GFG', 2.3]>

Les éléments de la liste sont accessibles via l'index attribué. Dans l'index de départ python de la liste, une séquence est 0 et l'index de fin est (si N éléments sont là) N-1.

Exemple : opérations de liste Python

# Creating a List with # the use of multiple values List = ['Geeks', 'For', 'Geeks'] print('
List containing multiple values: ') print(List) # Creating a Multi-Dimensional List # (By Nesting a list inside a List) List2 = [['Geeks', 'For'], ['Geeks']] print('
Multi-Dimensional List: ') print(List2) # accessing a element from the # list using index number print('Accessing element from the list') print(List[0]) print(List[2]) # accessing a element using # negative indexing print('Accessing element using negative indexing') # print the last element of list print(List[-1]) # print the third last element of list print(List[-3])>

List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks>

Tuple

Tuples Python sont similaires aux listes mais les tuples le sont immuable dans la nature, c'est-à-dire qu'une fois créé, il ne peut pas être modifié. Tout comme une liste, un tuple peut également contenir des éléments de différents types.

En Python, les tuples sont créés en plaçant une séquence de valeurs séparées par une « virgule » avec ou sans l'utilisation de parenthèses pour le regroupement de la séquence de données.

Note: Pour créer un tuple d'un élément, il doit y avoir une virgule finale. Par exemple, (8,) créera un tuple contenant 8 comme élément.

Exemple : opérations sur les tuples Python

# Creating a Tuple with # the use of Strings Tuple = ('Geeks', 'For') print('
Tuple with the use of String: ') print(Tuple) # Creating a Tuple with # the use of list list1 = [1, 2, 4, 5, 6] print('
Tuple using List: ') Tuple = tuple(list1) # Accessing element using indexing print('First element of tuple') print(Tuple[0]) # Accessing element from last # negative indexing print('
Last element of tuple') print(Tuple[-1]) print('
Third last element of tuple') print(Tuple[-3])>

Tuple with the use of String: ('Geeks', 'For') Tuple using List: First element of tuple 1 Last element of tuple 6 Third last element of tuple 4>

Ensemble

Ensemble Python est une collection de données mutable qui ne permet aucune duplication. Les ensembles sont essentiellement utilisés pour inclure des tests d’adhésion et éliminer les entrées en double. La structure de données utilisée ici est le hachage, une technique populaire pour effectuer l'insertion, la suppression et le parcours en O(1) en moyenne.

Si plusieurs valeurs sont présentes à la même position d'index, la valeur est ajoutée à cette position d'index pour former une liste chaînée. Dans, les ensembles CPython sont implémentés à l'aide d'un dictionnaire avec des variables factices, où les clés sont les membres définis avec de plus grandes optimisations de la complexité temporelle.

Définir la mise en œuvre :

Ensembles avec de nombreuses opérations sur une seule HashTable :

Exemple : opérations d'ensemble Python

# Creating a Set with # a mixed type of values # (Having numbers and strings) Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks']) print('
Set with the use of Mixed Values') print(Set) # Accessing element using # for loop print('
Elements of set: ') for i in Set: print(i, end =' ') print() # Checking the element # using in keyword print('Geeks' in Set)>

Set with the use of Mixed Values {1, 2, 4, 6, 'For', 'Geeks'} Elements of set: 1 2 4 6 For Geeks True>

Ensembles congelés

Ensembles congelés en Python, ce sont des objets immuables qui ne prennent en charge que les méthodes et les opérateurs qui produisent un résultat sans affecter le ou les ensembles gelés auxquels ils sont appliqués. Alors que les éléments d'un ensemble peuvent être modifiés à tout moment, les éléments de l'ensemble figé restent les mêmes après la création.

Exemple : ensemble Python gelé

# Same as {'a', 'b','c'} normal_set = set(['a', 'b','c']) print('Normal Set') print(normal_set) # A frozen set frozen_set = frozenset(['e', 'f', 'g']) print('
Frozen Set') print(frozen_set) # Uncommenting below line would cause error as # we are trying to add element to a frozen set # frozen_set.add('h')>

Normal Set {'a', 'b', 'c'} Frozen Set frozenset({'f', 'g', 'e'})>

Chaîne

Chaînes Python est le tableau immuable d'octets représentant les caractères Unicode. Python n'a pas de type de données caractère, un seul caractère est simplement une chaîne d'une longueur de 1.

Note: Les chaînes étant immuables, la modification d’une chaîne entraînera la création d’une nouvelle copie.

Exemple : opérations sur les chaînes Python

String = 'Welcome to GeeksForGeeks' print('Creating String: ') print(String) # Printing First character print('
First character of String is: ') print(String[0]) # Printing Last character print('
Last character of String is: ') print(String[-1])>

Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s>

Dictionnaire

Dictionnaire Python est une collection non ordonnée de données qui stocke les données au format d'une paire clé:valeur. C'est comme les tables de hachage dans n'importe quel autre langage avec la complexité temporelle de O(1). L'indexation du dictionnaire Python se fait à l'aide de clés. Il s'agit de n'importe quel type hachable, c'est-à-dire un objet qui ne peut jamais changer comme des chaînes, des nombres, des tuples, etc. Nous pouvons créer un dictionnaire en utilisant des accolades ({}) ou la compréhension du dictionnaire.

Exemple : opérations du dictionnaire Python

# Creating a Dictionary Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]} print('Creating Dictionary: ') print(Dict) # accessing a element using key print('Accessing a element using key:') print(Dict['Name']) # accessing a element using get() # method print('Accessing a element using get:') print(Dict.get(1)) # creation using Dictionary comprehension myDict = {x: x**2 for x in [1,2,3,4,5]} print(myDict)>

Creating Dictionary: {'Name': 'Geeks', 1: [1, 2, 3, 4]} Accessing a element using key: Geeks Accessing a element using get: [1, 2, 3, 4] {1: 1, 2: 4, 3: 9, 4: 16, 5: 25}>

Matrice

Une matrice est un tableau 2D où chaque élément est strictement de même taille. Pour créer une matrice, nous utiliserons le Paquet NumPy .

Exemple : opérations matricielles Python NumPy

import numpy as np a = np.array([[1,2,3,4],[4,55,1,2], [8,3,20,19],[11,2,22,21]]) m = np.reshape(a,(4, 4)) print(m) # Accessing element print('
Accessing Elements') print(a[1]) print(a[2][0]) # Adding Element m = np.append(m,[[1, 15,13,11]],0) print('
Adding Element') print(m) # Deleting Element m = np.delete(m,[1],0) print('
Deleting Element') print(m)>

Sortir

[[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]] Accessing Elements [ 4 55 1 2] 8 Adding Element [[ 1 2 3 4]  [ 4 55 1 2]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]] Deleting Element [[ 1 2 3 4]  [ 8 3 20 19]  [11 2 22 21]  [ 1 15 13 11]]>

Tableau d'octets

Python Bytearray donne une séquence mutable d'entiers compris entre 0 <= x < 256.

Exemple : opérations Python Bytearray

# Creating bytearray a = bytearray((12, 8, 25, 2)) print('Creating Bytearray:') print(a) # accessing elements print('
Accessing Elements:', a[1]) # modifying elements a[1] = 3 print('
After Modifying:') print(a) # Appending elements a.append(30) print('
After Adding Elements:') print(a)>

Creating Bytearray: bytearray(b'x0cx08x19x02') Accessing Elements: 8 After Modifying: bytearray(b'x0cx03x19x02') After Adding Elements: bytearray(b'x0cx03x19x02x1e')>

Liste liée

UN liste chaînée est une structure de données linéaire dans laquelle les éléments ne sont pas stockés à des emplacements mémoire contigus. Les éléments d'une liste chaînée sont liés à l'aide de pointeurs, comme indiqué dans l'image ci-dessous :

Une liste chaînée est représentée par un pointeur vers le premier nœud de la liste chaînée. Le premier nœud est appelé la tête. Si la liste chaînée est vide, alors la valeur de la tête est NULL. Chaque nœud d'une liste se compose d'au moins deux parties :

• Données
• Pointeur (ou référence) vers le nœud suivant

Exemple : définir une liste chaînée en Python

# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None>

Créons une simple liste chaînée avec 3 nœuds.

# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3)  '''  Three nodes have been created.  We have references to these three blocks as head,  second and third  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | None | | 2 | None | | 3 | None |  +----+------+ +----+------+ +----+------+  ''' llist.head.next = second; # Link first node with second  '''  Now next of first Node refers to second. So they  both are linked.  llist.head second third  | | |  | | |  +----+------+ +----+------+ +----+------+  | 1 | o-------->| 2 | nul | | 3 | nul |  +----+------+ +----+------+ +----+------+ ''' seconde.suivant = troisième ; # Lier le deuxième nœud au troisième nœud ''' Maintenant, le prochain nœud du deuxième nœud fait référence au troisième. Les trois nœuds sont donc liés.  llist.head deuxième tiers | | |  | | |  +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | nul |  +----+------+ +----+------+ +----+------+ '''>

Parcours de liste chaînée

Dans le programme précédent, nous avons créé une simple liste chaînée avec trois nœuds. Parcourons la liste créée et imprimons les données de chaque nœud. Pour le parcours, écrivons une fonction à usage général printList() qui imprime n'importe quelle liste donnée.

# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()>

1 2 3>

Plus d'articles sur la liste chaînée

• Insertion de liste chaînée
• Suppression de liste liée (suppression d'une clé donnée)
• Suppression de liste liée (suppression d'une clé à une position donnée)
• Trouver la longueur d'une liste chaînée (itérative et récursive)
• Rechercher un élément dans une liste chaînée (itérative et récursive)
• Nième nœud à partir de la fin d'une liste chaînée
• Inverser une liste chaînée

UN empiler est une structure de données linéaire qui stocke les éléments selon la méthode Last-In/First-Out (LIFO) ou First-In/Last-Out (FILO). Dans la pile, un nouvel élément est ajouté à une extrémité et un élément est supprimé à cette extrémité uniquement. Les opérations d'insertion et de suppression sont souvent appelées push et pop.

stack = [] # append() function to push # element in the stack stack.append('g') stack.append('f') stack.append('g') print('Initial stack') print(stack) # pop() function to pop # element from stack in # LIFO order print('
Elements popped from stack:') print(stack.pop()) print(stack.pop()) print(stack.pop()) print('
Stack after elements are popped:') print(stack) # uncommenting print(stack.pop()) # will cause an IndexError # as the stack is now empty>

Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []>

En tant que pile, le file d'attente est une structure de données linéaire qui stocke les éléments selon le principe premier entré, premier sorti (FIFO). Avec une file d'attente, l'élément ajouté le moins récemment est supprimé en premier. Un bon exemple de file d'attente est n'importe quelle file d'attente de consommateurs pour une ressource dans laquelle le consommateur arrivé en premier est servi en premier.

# Initializing a queue queue = [] # Adding elements to the queue queue.append('g') queue.append('f') queue.append('g') print('Initial queue') print(queue) # Removing elements from the queue print('
Elements dequeued from queue') print(queue.pop(0)) print(queue.pop(0)) print(queue.pop(0)) print('
Queue after removing elements') print(queue) # Uncommenting print(queue.pop(0)) # will raise and IndexError # as the queue is now empty>

Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []>

Files d'attente prioritaires sont des structures de données abstraites où chaque donnée/valeur dans la file d'attente a une certaine priorité. Par exemple, dans les compagnies aériennes, les bagages portant le titre Business ou First class arrivent plus tôt que les autres. La file d'attente prioritaire est une extension de la file d'attente avec les propriétés suivantes.

• Un élément de priorité élevée est retiré de la file d'attente avant un élément de priorité faible.
• Si deux éléments ont la même priorité, ils sont servis selon leur ordre dans la file d'attente.

# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i]>self.queue[max] : max = i item = self.queue[max] del self.queue[max] renvoie l'élément sauf IndexError : print() exit() si __name__ == '__main__' : myQueue = PriorityQueue( ) myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) while not myQueue.isEmpty() : print(myQueue.delete())>

12 1 14 7 14 12 7 1>

Tas

module heapq en Python fournit la structure de données de tas qui est principalement utilisée pour représenter une file d'attente prioritaire. La propriété de cette structure de données est qu'elle donne toujours le plus petit élément (tas min) chaque fois que l'élément est extrait. Chaque fois que des éléments sont poussés ou sautés, la structure du tas est conservée. L'élément heap[0] renvoie également le plus petit élément à chaque fois. Il prend en charge l'extraction et l'insertion du plus petit élément dans les temps O (log n).

Généralement, les tas peuvent être de deux types :

• Tas maximum : Dans un Max-Heap, la clé présente au niveau du nœud racine doit être la plus grande parmi les clés présentes chez tous ses enfants. La même propriété doit être vraie de manière récursive pour tous les sous-arbres de cet arbre binaire.
• Tas minimum : Dans un Min-Heap, la clé présente sur le nœud racine doit être la clé minimale parmi les clés présentes sur tous ses enfants. La même propriété doit être vraie de manière récursive pour tous les sous-arbres de cet arbre binaire.

# importing 'heapq' to implement heap queue import heapq # initializing list li = [5, 7, 9, 1, 3] # using heapify to convert list into heap heapq.heapify(li) # printing created heap print ('The created heap is : ',end='') print (list(li)) # using heappush() to push elements into heap # pushes 4 heapq.heappush(li,4) # printing modified heap print ('The modified heap after push is : ',end='') print (list(li)) # using heappop() to pop smallest element print ('The popped and smallest element is : ',end='') print (heapq.heappop(li))>

The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1>

Plus d'articles sur le tas

• Tas binaire
• K'ième plus grand élément d'un tableau
• K'th plus petit/plus grand élément dans un tableau non trié
• Trier un tableau presque trié
• K-ième sous-tableau contigu à la plus grande somme
• Somme minimale de deux nombres formés à partir des chiffres d'un tableau

Un arbre est une structure de données hiérarchique qui ressemble à la figure ci-dessous :

 tree  ----  j <-- root  /   f k  /   a h z <-- leaves>

Le nœud le plus haut de l’arborescence est appelé racine tandis que les nœuds les plus bas ou les nœuds sans enfants sont appelés nœuds feuilles. Les nœuds qui se trouvent directement sous un nœud sont appelés ses enfants et les nœuds qui se trouvent directement au-dessus de quelque chose sont appelés son parent.

UN arbre binaire est un arbre dont les éléments peuvent avoir près de deux enfants. Étant donné que chaque élément d’un arbre binaire ne peut avoir que 2 enfants, nous les nommons généralement enfants gauche et droit. Un nœud d'arbre binaire contient les parties suivantes.

• Données
• Pointeur vers l'enfant gauche
• Pointeur vers le bon enfant

Exemple : définition d'une classe de nœud

# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key>

Créons maintenant un arbre à 4 nœuds en Python. Supposons que la structure arborescente ressemble à ci-dessous :

 tree  ----  1 <-- root  /   2 3   /  4>

Exemple : ajout de données à l'arborescence

# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement  1  /   None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1  1  /   2 3  /  /  None None None None''' root.left.left = Node(4); '''4 becomes left child of 2  1  /   2 3  /  /  4 None None None /  None None'''>

Traversée des arbres

Les arbres peuvent être traversés en différentes manières. Voici les méthodes généralement utilisées pour parcourir les arbres. Considérons l'arbre ci-dessous -

 tree  ----  1 <-- root  /   2 3   /  4 5>

Premières traversées en profondeur :

• Dans l'ordre (Gauche, Racine, Droite) : 4 2 5 1 3
• Précommande (Racine, Gauche, Droite) : 1 2 4 5 3
• Post-ordre (Gauche, Droite, Racine) : 4 5 2 3 1

Ordre de l'algorithme (arbre)

• Parcourez le sous-arbre gauche, c'est-à-dire appelez Inorder (sous-arbre gauche)
• Visitez la racine.
• Parcourez le sous-arbre droit, c'est-à-dire appelez Inorder (sous-arbre droit)

Précommande d'algorithme (arbre)

• Visitez la racine.
• Parcourez le sous-arbre gauche, c'est-à-dire appelez Preorder(left-subtree)
• Parcourez le sous-arbre droit, c'est-à-dire appelez Preorder (sous-arbre droit)

Algorithme Mandat postal (arbre)

• Parcourez le sous-arbre gauche, c'est-à-dire appelez Postorder (sous-arbre gauche)
• Parcourez le sous-arbre droit, c'est-à-dire appelez Postorder (sous-arbre droit)
• Visitez la racine.

# Python program to for tree traversals # A class that represents an individual node in a # Binary Tree class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A function to do inorder tree traversal def printInorder(root): if root: # First recur on left child printInorder(root.left) # then print the data of node print(root.val), # now recur on right child printInorder(root.right) # A function to do postorder tree traversal def printPostorder(root): if root: # First recur on left child printPostorder(root.left) # the recur on right child printPostorder(root.right) # now print the data of node print(root.val), # A function to do preorder tree traversal def printPreorder(root): if root: # First print the data of node print(root.val), # Then recur on left child printPreorder(root.left) # Finally recur on right child printPreorder(root.right) # Driver code root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Preorder traversal of binary tree is') printPreorder(root) print('
Inorder traversal of binary tree is') printInorder(root) print('
Postorder traversal of binary tree is') printPostorder(root)>

Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1>

Complexité temporelle – O(n)

Traversée d'ordre en largeur ou en niveau

Parcours de l'ordre de niveau d'un arbre est un parcours en largeur d'abord pour l'arbre. Le parcours d’ordre de niveau de l’arbre ci-dessus est 1 2 3 4 5.

Pour chaque nœud, le nœud est d'abord visité, puis ses nœuds enfants sont placés dans une file d'attente FIFO. Vous trouverez ci-dessous l’algorithme pour le même –

• Créer une file d'attente vide q
• temp_node = root /*démarrer à partir de root*/
• Boucle pendant que temp_node n'est pas NULL
  • print temp_node->data.
  • Mettre les enfants de temp_node en file d'attente (premiers enfants à gauche puis à droite) vers q
  • Retirer un nœud de q

# Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self ,key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Imprimer le début de la file d'attente et # le supprimer de la file d'attente print (queue[0].data) node = queue.pop(0) # Mettre l'enfant gauche en file d'attente si node.left n'est pas Aucun : queue.append(node.left ) # Mettre l'enfant droit en file d'attente si node.right n'est pas Aucun : queue.append(node.right) # Programme pilote pour tester la fonction ci-dessus root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print ('La traversée de l'ordre de niveau de l'arbre binaire est -') printLevelOrder(root)>

Level Order Traversal of binary tree is - 1 2 3 4 5>

Complexité temporelle : O(n)

Plus d'articles sur l'arbre binaire

• Insertion dans un arbre binaire
• Suppression dans un arbre binaire
• Traversée d'arbre dans l'ordre sans récursion
• Inorder Tree Traversal sans récursion et sans stack !
• Imprimer le parcours de post-commande à partir des parcours d'ordre et de pré-commande donnés
• Trouver le parcours post-commande de BST à partir du parcours de précommande

Arbre de recherche binaire est une structure de données arborescente binaire basée sur des nœuds qui possède les propriétés suivantes :

exemples de systèmes d'exploitation

Les propriétés ci-dessus de l'arbre de recherche binaire fournissent un classement parmi les clés afin que les opérations telles que la recherche, le minimum et le maximum puissent être effectuées rapidement. S'il n'y a pas d'ordre, nous devrons alors comparer chaque clé pour rechercher une clé donnée.

Élément de recherche

• Commencez par la racine.
• Comparez l'élément de recherche avec root, s'il est inférieur à root, puis récurez pour la gauche, sinon récurez pour la droite.
• Si l’élément à rechercher est trouvé n’importe où, renvoyez vrai, sinon renvoyez faux.

# A utility function to search a given key in BST def search(root,key): # Base Cases: root is null or key is present at root if root is None or root.val == key: return root # Key is greater than root's key if root.val < key: return search(root.right,key) # Key is smaller than root's key return search(root.left,key)>

Insertion d'une clé

• Commencez par la racine.
• Comparez l'élément d'insertion avec root, s'il est inférieur à root, alors récurez pour la gauche, sinon récurez pour la droite.
• Après avoir atteint la fin, insérez simplement ce nœud à gauche (s'il est inférieur à l'actuel) sinon à droite.

# Python program to demonstrate # insert operation in binary search tree # A utility class that represents # an individual node in a BST class Node: def __init__(self, key): self.left = None self.right = None self.val = key # A utility function to insert # a new node with the given key def insert(root, key): if root is None: return Node(key) else: if root.val == key: return root elif root.val < key: root.right = insert(root.right, key) else: root.left = insert(root.left, key) return root # A utility function to do inorder tree traversal def inorder(root): if root: inorder(root.left) print(root.val) inorder(root.right) # Driver program to test the above functions # Let us create the following BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 r = Node(50) r = insert(r, 30) r = insert(r, 20) r = insert(r, 40) r = insert(r, 70) r = insert(r, 60) r = insert(r, 80) # Print inorder traversal of the BST inorder(r)>

20 30 40 50 60 70 80>

Plus d'articles sur l'arbre de recherche binaire

• Arbre de recherche binaire – Supprimer la clé
• Construire BST à partir d'un parcours de précommande donné | Ensemble 1
• Conversion d'un arbre binaire en arbre de recherche binaire
• Trouver le nœud avec la valeur minimale dans un arbre de recherche binaire
• Un programme pour vérifier si un arbre binaire est BST ou non

UN graphique est une structure de données non linéaire composée de nœuds et d'arêtes. Les nœuds sont parfois également appelés sommets et les arêtes sont des lignes ou des arcs qui relient deux nœuds quelconques du graphique. Plus formellement, un graphe peut être défini comme un graphe constitué d'un ensemble fini de sommets (ou nœuds) et d'un ensemble d'arêtes qui relient une paire de nœuds.

# A simple representation of graph using Adjacency Matrix class Graph: def __init__(self,numvertex): self.adjMatrix = [[-1]*numvertex for x in range(numvertex)] self.numvertex = numvertex self.vertices = {} self.verticeslist =[0]*numvertex def set_vertex(self,vtx,id): if 0<=vtx<=self.numvertex: self.vertices[id] = vtx self.verticeslist[vtx] = id def set_edge(self,frm,to,cost=0): frm = self.vertices[frm] to = self.vertices[to] self.adjMatrix[frm][to] = cost # for directed graph do not add this self.adjMatrix[to][frm] = cost def get_vertex(self): return self.verticeslist def get_edges(self): edges=[] for i in range (self.numvertex): for j in range (self.numvertex): if (self.adjMatrix[i][j]!=-1): edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j])) return edges def get_matrix(self): return self.adjMatrix G =Graph(6) G.set_vertex(0,'a') G.set_vertex(1,'b') G.set_vertex(2,'c') G.set_vertex(3,'d') G.set_vertex(4,'e') G.set_vertex(5,'f') G.set_edge('a','e',10) G.set_edge('a','c',20) G.set_edge('c','b',30) G.set_edge('b','e',40) G.set_edge('e','d',50) G.set_edge('f','e',60) print('Vertices of Graph') print(G.get_vertex()) print('Edges of Graph') print(G.get_edges()) print('Adjacency Matrix of Graph') print(G.get_matrix())>

# A class to represent the adjacency list of the node class AdjNode: def __init__(self, data): self.vertex = data self.next = None # A class to represent a graph. A graph # is the list of the adjacency lists. # Size of the array will be the no. of the # vertices 'V' class Graph: def __init__(self, vertices): self.V = vertices self.graph = [None] * self.V # Function to add an edge in an undirected graph def add_edge(self, src, dest): # Adding the node to the source node node = AdjNode(dest) node.next = self.graph[src] self.graph[src] = node # Adding the source node to the destination as # it is the undirected graph node = AdjNode(src) node.next = self.graph[dest] self.graph[dest] = node # Function to print the graph def print_graph(self): for i in range(self.V): print('Adjacency list of vertex {}
 head'.format(i), end='') temp = self.graph[i] while temp: print(' ->{}'.format(temp.vertex), end='') temp = temp.next print(' 
') # Programme pilote vers la classe graphique ci-dessus si __name__ == '__main__' : V = 5 graphique = Graphique(V) graph.add_edge(0, 1) graph.add_edge(0, 4) graph.add_edge(1, 2) graph.add_edge(1, 3) graph.add_edge(1, 4) graph.add_edge(2, 3) graph.add_edge(3, 4) graph.print_graph()>

Adjacency list of vertex 0 head ->4 -> 1 Liste de contiguïté de la tête du sommet 1 -> 4 -> 3 -> 2 -> 0 Liste de contiguïté de la tête du sommet 2 -> 3 -> 1 Liste de contiguïté de la tête du sommet 3 -> 4 -> 2 -> 1 Adjacence liste des sommets 4 tête -> 3 -> 1 -> 0>

Traversée en largeur car un graphique est similaire au parcours en largeur d'abord d'un arbre. Le seul problème ici est que, contrairement aux arbres, les graphiques peuvent contenir des cycles, nous pouvons donc revenir au même nœud. Pour éviter de traiter un nœud plus d'une fois, nous utilisons un tableau booléen visité. Pour simplifier, on suppose que tous les sommets sont accessibles à partir du sommet de départ.

Par exemple, dans le graphique suivant, nous commençons le parcours à partir du sommet 2. Lorsque nous arrivons au sommet 0, nous recherchons tous les sommets adjacents de celui-ci. 2 est également un sommet adjacent de 0. Si nous ne marquons pas les sommets visités, alors 2 sera à nouveau traité et deviendra un processus sans fin. Un parcours en largeur du graphique suivant est 2, 0, 3, 1.

# Python3 Program to print BFS traversal # from a given source vertex. BFS(int s) # traverses vertices reachable from s. from collections import defaultdict # This class represents a directed graph # using adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self,u,v): self.graph[u].append(v) # Function to print a BFS of graph def BFS(self, s): # Mark all the vertices as not visited visited = [False] * (max(self.graph) + 1) # Create a queue for BFS queue = [] # Mark the source node as # visited and enqueue it queue.append(s) visited[s] = True while queue: # Dequeue a vertex from # queue and print it s = queue.pop(0) print (s, end = ' ') # Get all adjacent vertices of the # dequeued vertex s. If a adjacent # has not been visited, then mark it # visited and enqueue it for i in self.graph[s]: if visited[i] == False: queue.append(i) visited[i] = True # Driver code # Create a graph given in # the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print ('Following is Breadth First Traversal' ' (starting from vertex 2)') g.BFS(2)>

Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1>

Complexité temporelle : O(V+E) où V est le nombre de sommets du graphe et E est le nombre d'arêtes du graphe.

Recherche en profondeur d'abord ou DFS

Première traversée en profondeur car un graphique est similaire au Depth First Traversal d’un arbre. Le seul problème ici est que, contrairement aux arbres, les graphiques peuvent contenir des cycles, un nœud peut être visité deux fois. Pour éviter de traiter un nœud plus d'une fois, utilisez un tableau booléen visité.

Algorithme:

• Créez une fonction récursive qui prend l'index du nœud et un tableau visité.
• Marquez le nœud actuel comme visité et imprimez le nœud.
• Parcourez tous les nœuds adjacents et non marqués et appelez la fonction récursive avec l'index du nœud adjacent.

# Python3 program to print DFS traversal # from a given graph from collections import defaultdict # This class represents a directed graph using # adjacency list representation class Graph: # Constructor def __init__(self): # default dictionary to store graph self.graph = defaultdict(list) # function to add an edge to graph def addEdge(self, u, v): self.graph[u].append(v) # A function used by DFS def DFSUtil(self, v, visited): # Mark the current node as visited # and print it visited.add(v) print(v, end=' ') # Recur for all the vertices # adjacent to this vertex for neighbour in self.graph[v]: if neighbour not in visited: self.DFSUtil(neighbour, visited) # The function to do DFS traversal. It uses # recursive DFSUtil() def DFS(self, v): # Create a set to store visited vertices visited = set() # Call the recursive helper function # to print DFS traversal self.DFSUtil(v, visited) # Driver code # Create a graph given # in the above diagram g = Graph() g.addEdge(0, 1) g.addEdge(0, 2) g.addEdge(1, 2) g.addEdge(2, 0) g.addEdge(2, 3) g.addEdge(3, 3) print('Following is DFS from (starting from vertex 2)') g.DFS(2)>

Following is DFS from (starting from vertex 2) 2 0 1 3>

Plus d'articles sur le graphique

• Représentations graphiques utilisant set et hash
• Trouver le sommet mère dans un graphique
• Recherche itérative en profondeur d'abord
• Comptez le nombre de nœuds à un niveau donné dans un arbre à l'aide de BFS
• Compter tous les chemins possibles entre deux sommets

Le processus dans lequel une fonction s'appelle directement ou indirectement est appelé récursivité et la fonction correspondante est appelée un fonction récursive . Grâce aux algorithmes récursifs, certains problèmes peuvent être résolus assez facilement. Des exemples de tels problèmes sont les Tours de Hanoï (TOH), les traversées d'arbres Inorder/Preorder/Postorder, DFS of Graph, etc.

def fact(n):  # base case  if (n <= 1)   return 1  else   return n*fact(n-1)>

erreur d'exécution

Comment la mémoire est allouée aux différents appels de fonction en récursion ?

Lorsqu'une fonction est appelée depuis main(), la mémoire lui est allouée sur la pile. Une fonction récursive s'appelle elle-même, la mémoire d'une fonction appelée est allouée en plus de la mémoire allouée à la fonction appelante et une copie différente des variables locales est créée pour chaque appel de fonction. Lorsque le cas de base est atteint, la fonction renvoie sa valeur à la fonction par laquelle elle est appelée et la mémoire est désallouée et le processus continue.

Prenons l'exemple du fonctionnement de la récursivité en prenant une fonction simple.

# A Python 3 program to # demonstrate working of # recursion def printFun(test): if (test < 1): return else: print(test, end=' ') printFun(test-1) # statement 2 print(test, end=' ') return # Driver Code test = 3 printFun(test)>

3 2 1 1 2 3>

La pile mémoire a été représentée dans le diagramme ci-dessous.

Plus d'articles sur la récursivité

• Récursivité
• Récursivité en Python
• Questions pratiques pour la récursivité | Ensemble 1
• Questions pratiques pour la récursivité | Ensemble 2
• Questions pratiques pour la récursivité | Ensemble 3
• Questions pratiques pour la récursivité | Ensemble 4
• Questions pratiques pour la récursivité | Ensemble 5
• Questions pratiques pour la récursivité | Ensemble 6
• Questions pratiques pour la récursivité | Ensemble 7

>>> Plus

Programmation dynamique

Programmation dynamique est principalement une optimisation par rapport à la simple récursion. Partout où nous voyons une solution récursive qui nécessite des appels répétés pour les mêmes entrées, nous pouvons l'optimiser à l'aide de la programmation dynamique. L’idée est de simplement stocker les résultats des sous-problèmes, afin que nous n’ayons pas à les recalculer en cas de besoin ultérieur. Cette optimisation simple réduit les complexités temporelles d'exponentielle à polynomiale. Par exemple, si nous écrivons une solution récursive simple pour les nombres de Fibonacci, nous obtenons une complexité temporelle exponentielle et si nous l'optimisons en stockant les solutions des sous-problèmes, la complexité temporelle se réduit à linéaire.

Tabulation vs mémorisation

Il existe deux manières différentes de stocker les valeurs afin que les valeurs d'un sous-problème puissent être réutilisées. Ici, nous discuterons de deux modèles de résolution de problèmes de programmation dynamique (DP) :

• Tabulation: De bas en haut
• Mémorisation : De haut en bas

Tabulation

Comme son nom l’indique, commencer par le bas et accumuler les réponses vers le haut. Discutons en termes de transition d’état.

Décrivons un état pour notre problème DP comme étant dp[x] avec dp[0] comme état de base et dp[n] comme état de destination. Nous devons donc trouver la valeur de l'état de destination, c'est-à-dire dp[n].

Si nous commençons notre transition à partir de notre état de base, c'est-à-dire dp[0] et suivons notre relation de transition d'état pour atteindre notre état de destination dp[n], nous l'appelons l'approche Bottom-Up car il est clair que nous avons commencé notre transition depuis le état de base inférieur et atteint l’état souhaité le plus élevé.

Maintenant, pourquoi appelons-nous cela méthode de tabulation ?

Pour savoir cela, écrivons d’abord du code pour calculer la factorielle d’un nombre en utilisant une approche ascendante. Encore une fois, comme procédure générale pour résoudre un DP, nous définissons d’abord un état. Dans ce cas, nous définissons un état comme dp[x], où dp[x] doit trouver la factorielle de x.

Or, il est bien évident que dp[x+1] = dp[x] * (x+1)

# Tabulated version to find factorial x. dp = [0]*MAXN # base case dp[0] = 1; for i in range(n+1):  dp[i] = dp[i-1] * i>

Mémorisation

Encore une fois, décrivons-le en termes de transition d’état. Si nous avons besoin de trouver la valeur d'un état, disons dp[n] et au lieu de partir de l'état de base, c'est-à-dire dp[0], nous demandons notre réponse aux états qui peuvent atteindre l'état de destination dp[n] après la transition d'état. relation, alors c'est la mode descendante du DP.

Ici, nous commençons notre voyage à partir de l'état de destination le plus haut et calculons sa réponse en prenant en compte les valeurs des états qui peuvent atteindre l'état de destination, jusqu'à ce que nous atteignions l'état de base le plus bas.

Encore une fois, écrivons le code du problème factoriel de manière descendante.

# Memoized version to find factorial x. # To speed up we store the values # of calculated states # initialized to -1 dp[0]*MAXN # return fact x! def solve(x):  if (x==0)  return 1  if (dp[x]!=-1)  return dp[x]  return (dp[x] = x * solve(x-1))>

Plus d'articles sur la programmation dynamique

• Propriété de sous-structure optimale
• Propriété de sous-problèmes superposés
• Numéros de Fibonacci
• Sous-ensemble de somme divisible par m
• Sous-séquence croissante de somme maximale
• Sous-chaîne commune la plus longue

>>> Plus

Algorithmes de recherche

Recherche linéaire

• Commencez par l'élément le plus à gauche de arr[] et comparez un par un x avec chaque élément de arr[]
• Si x correspond à un élément, renvoie l'index.
• Si x ne correspond à aucun des éléments, renvoie -1.

# Python3 code to linearly search x in arr[]. # If x is present then return its location, # otherwise return -1 def search(arr, n, x): for i in range(0, n): if (arr[i] == x): return i return -1 # Driver Code arr = [2, 3, 4, 10, 40] x = 10 n = len(arr) # Function call result = search(arr, n, x) if(result == -1): print('Element is not present in array') else: print('Element is present at index', result)>

Element is present at index 3>

La complexité temporelle de l'algorithme ci-dessus est O(n).

tests manuels

Pour plus d'informations, reportez-vous à Recherche linéaire .

Recherche binaire

Recherchez un tableau trié en divisant à plusieurs reprises l'intervalle de recherche en deux. Commencez par un intervalle couvrant l’ensemble du tableau. Si la valeur de la clé de recherche est inférieure à l'élément au milieu de l'intervalle, réduisez l'intervalle à la moitié inférieure. Sinon, réduisez-le à la moitié supérieure. Vérifiez à plusieurs reprises jusqu'à ce que la valeur soit trouvée ou que l'intervalle soit vide.

# Python3 Program for recursive binary search. # Returns index of x in arr if present, else -1 def binarySearch (arr, l, r, x): # Check base case if r>= l: mid = l + (r - l) // 2 # Si l'élément est présent au milieu lui-même if arr[mid] == x: return mid # Si l'élément est plus petit que mid, alors il # ne peut être présent dans le sous-tableau gauche elif arr[mid]> x : return binaireSearch(arr, l, mid-1, x) # Sinon, l'élément ne peut être présent que # dans le sous-tableau droit sinon : return binaireSearch(arr, mid + 1, r, x ) else : # L'élément n'est pas présent dans le tableau return -1 # Driver Code arr = [ 2, 3, 4, 10, 40 ] x = 10 # Résultat de l'appel de fonction = binaireSearch(arr, 0, len(arr)-1 , x) si résultat != -1 : print ('L'élément est présent à l'index % d' % result) sinon : print ('L'élément n'est pas présent dans le tableau')>

Element is present at index 3>

La complexité temporelle de l'algorithme ci-dessus est O(log(n)).

Pour plus d'informations, reportez-vous à Recherche binaire .

Algorithmes de tri

Tri de sélection

Le tri par sélection L'algorithme trie un tableau en recherchant à plusieurs reprises l'élément minimum (en tenant compte de l'ordre croissant) de la partie non triée et en le plaçant au début. À chaque itération du tri par sélection, l'élément minimum (en tenant compte de l'ordre croissant) du sous-tableau non trié est sélectionné et déplacé vers le sous-tableau trié.

Organigramme du tri par sélection :

# Python program for implementation of Selection # Sort import sys A = [64, 25, 12, 22, 11] # Traverse through all array elements for i in range(len(A)): # Find the minimum element in remaining # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx]>A[j]: min_idx = j # Échangez l'élément minimum trouvé avec # le premier élément A[i], A[min_idx] = A[min_idx], A[i] # Code du pilote à tester ci-dessus, impression ('Tableau trié ') pour i dans range(len(A)) : print('%d' %A[i]),>

Sorted array 11 12 22 25 64>

Complexité temporelle : Sur²) car il y a deux boucles imbriquées.

Espace auxiliaire : O(1)

Tri à bulles

Tri à bulles est l'algorithme de tri le plus simple qui fonctionne en échangeant à plusieurs reprises les éléments adjacents s'ils sont dans le mauvais ordre.

Illustration :

# Python program for implementation of Bubble Sort def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # Last i elements are already in place for j in range(0, n-i-1): # traverse the array from 0 to n-i-1 # Swap if the element found is greater # than the next element if arr[j]>arr[j+1] : arr[j], arr[j+1] = arr[j+1], arr[j] # Code du pilote à tester ci-dessus arr = [64, 34, 25, 12, 22, 11 , 90] bubbleSort(arr) print ('Le tableau trié est :') pour i dans la plage(len(arr)) : print ('%d' %arr[i]),>

Sorted array is: 11 12 22 25 34 64 90>

Complexité temporelle : Sur²)

Tri par insertion

Pour trier un tableau de taille n par ordre croissant en utilisant tri par insertion :

• Itérer de arr[1] à arr[n] sur le tableau.
• Comparez l'élément actuel (clé) à son prédécesseur.
• Si l'élément clé est plus petit que son prédécesseur, comparez-le aux éléments précédents. Déplacez les éléments les plus grands d'une position vers le haut pour libérer de l'espace pour l'élément échangé.

Illustration:

# Python program for implementation of Insertion Sort # Function to do insertion sort def insertionSort(arr): # Traverse through 1 to len(arr) for i in range(1, len(arr)): key = arr[i] # Move elements of arr[0..i-1], that are # greater than key, to one position ahead # of their current position j = i-1 while j>= 0 et clé< arr[j] : arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key # Driver code to test above arr = [12, 11, 13, 5, 6] insertionSort(arr) for i in range(len(arr)): print ('% d' % arr[i])>

 5 6 11 12 13>

Complexité temporelle : Sur²))

Tri par fusion

Comme QuickSort, Tri par fusion est un algorithme Divide and Conquer. Il divise le tableau d'entrée en deux moitiés, s'appelle lui-même pour les deux moitiés, puis fusionne les deux moitiés triées. La fonction merge() est utilisée pour fusionner deux moitiés. La fusion (arr, l, m, r) est un processus clé qui suppose que arr[l..m] et arr[m+1..r] sont triés et fusionne les deux sous-tableaux triés en un seul.

MergeSort(arr[], l, r) If r>l 1. Trouvez le point médian pour diviser le tableau en deux moitiés : middle m = l+ (r-l)/2 2. Appelez mergeSort pour la première moitié : Appelez mergeSort(arr, l, m) 3. Appelez mergeSort pour la seconde moitié : Appelez mergeSort(arr, m+1, r) 4. Fusionnez les deux moitiés triées aux étapes 2 et 3 : Appelez merge(arr, l, m, r)>

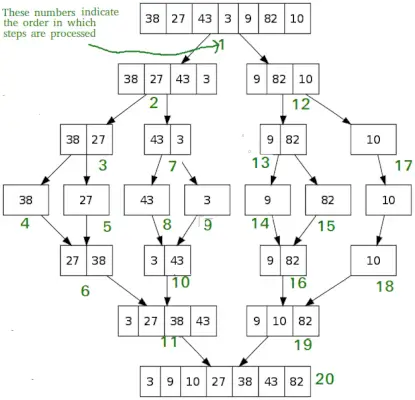
# Python program for implementation of MergeSort def mergeSort(arr): if len(arr)>1: # Trouver le milieu du tableau mid = len(arr)//2 # Diviser les éléments du tableau L = arr[:mid] # en 2 moitiés R = arr[mid:] # Trier la première moitié mergeSort(L) # Tri de la seconde moitié mergeSort(R) i = j = k = 0 # Copier les données dans les tableaux temporaires L[] et R[] pendant que i< len(L) and j < len(R): if L[i] < R[j]: arr[k] = L[i] i += 1 else: arr[k] = R[j] j += 1 k += 1 # Checking if any element was left while i < len(L): arr[k] = L[i] i += 1 k += 1 while j < len(R): arr[k] = R[j] j += 1 k += 1 # Code to print the list def printList(arr): for i in range(len(arr)): print(arr[i], end=' ') print() # Driver Code if __name__ == '__main__': arr = [12, 11, 13, 5, 6, 7] print('Given array is', end='
') printList(arr) mergeSort(arr) print('Sorted array is: ', end='
') printList(arr)>

Given array is 12 11 13 5 6 7 Sorted array is: 5 6 7 11 12 13>

Complexité temporelle : O(n(logn))

Tri rapide

Comme le tri par fusion, Tri rapide est un algorithme Divide and Conquer. Il choisit un élément comme pivot et partitionne le tableau donné autour du pivot choisi. Il existe de nombreuses versions différentes de quickSort qui sélectionnent le pivot de différentes manières.

Choisissez toujours le premier élément comme pivot.

• Choisissez toujours le dernier élément comme pivot (implémenté ci-dessous)
• Choisissez un élément aléatoire comme pivot.
• Choisissez la médiane comme pivot.

Le processus clé dans quickSort est partition(). La cible des partitions est, étant donné un tableau et un élément x du tableau comme pivot, de placer x à sa position correcte dans le tableau trié et de placer tous les éléments plus petits (plus petits que x) avant x, et de placer tous les éléments plus grands (supérieurs à x) après X. Tout cela doit se faire en temps linéaire.

/* low -->Index de début, élevé --> Index de fin */ quickSort(arr[], low, high) { if (low { /* pi est l'index de partitionnement, arr[pi] est maintenant au bon endroit */ pi = partition(arr, low, high); quickSort(arr, low, pi - 1); // Avant pi quickSort(arr, pi + 1, high); // Après pi } }>

Algorithme de partition

Il peut y avoir de nombreuses façons de procéder à une partition, en suivant pseudo-code adopte la méthode donnée dans le livre CLRS. La logique est simple, nous partons de l'élément le plus à gauche et gardons une trace de l'index des éléments plus petits (ou égaux) comme i. Lors du parcours, si nous trouvons un élément plus petit, nous échangeons l'élément actuel avec arr[i]. Sinon, nous ignorons l'élément actuel.

/* This function takes last element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than pivot) to left of pivot and all greater elements to right of pivot */ partition (arr[], low, high) {  // pivot (Element to be placed at right position)  pivot = arr[high];   i = (low – 1) // Index of smaller element and indicates the   // right position of pivot found so far  for (j = low; j <= high- 1; j++){  // If current element is smaller than the pivot  if (arr[j]   i++; // increment index of smaller element  swap arr[i] and arr[j]  }  }  swap arr[i + 1] and arr[high])  return (i + 1) }>

# Python3 implementation of QuickSort # This Function handles sorting part of quick sort # start and end points to first and last element of # an array respectively def partition(start, end, array): # Initializing pivot's index to start pivot_index = start pivot = array[pivot_index] # This loop runs till start pointer crosses # end pointer, and when it does we swap the # pivot with element on end pointer while start < end: # Increment the start pointer till it finds an # element greater than pivot while start < len(array) and array[start] <= pivot: start += 1 # Decrement the end pointer till it finds an # element less than pivot while array[end]>pivot: end -= 1 # Si le début et la fin ne se sont pas croisés, # échangez les nombres au début et à la fin if(start< end): array[start], array[end] = array[end], array[start] # Swap pivot element with element on end pointer. # This puts pivot on its correct sorted place. array[end], array[pivot_index] = array[pivot_index], array[end] # Returning end pointer to divide the array into 2 return end # The main function that implements QuickSort def quick_sort(start, end, array): if (start < end): # p is partitioning index, array[p] # is at right place p = partition(start, end, array) # Sort elements before partition # and after partition quick_sort(start, p - 1, array) quick_sort(p + 1, end, array) # Driver code array = [ 10, 7, 8, 9, 1, 5 ] quick_sort(0, len(array) - 1, array) print(f'Sorted array: {array}')>

Sorted array: [1, 5, 7, 8, 9, 10]>

Complexité temporelle : O(n(logn))

Tri Shell

Tri Shell est principalement une variante du tri par insertion. Dans le tri par insertion, nous déplaçons les éléments d’une seule position vers l’avant. Lorsqu’un élément doit être avancé très loin, de nombreux mouvements sont impliqués. L'idée de shellSort est de permettre l'échange d'articles éloignés. Dans shellSort, nous trions le tableau en h pour une grande valeur de h. Nous continuons à réduire la valeur de h jusqu'à ce qu'elle devienne 1. Un tableau est dit trié en h si toutes les sous-listes de chaque h^èmel’élément est trié.

# Python3 program for implementation of Shell Sort def shellSort(arr): gap = len(arr) // 2 # initialize the gap while gap>0 : i = 0 j = écart # vérifie le tableau de gauche à droite # jusqu'au dernier index possible de j pendant que j< len(arr): if arr[i]>arr[j]: arr[i],arr[j] = arr[j],arr[i] i += 1 j += 1 # maintenant, nous regardons en arrière depuis le ième index vers la gauche # nous échangeons les valeurs qui ne sont pas dans le bon ordre. k = i tandis que k - écart> -1 : si arr[k - écart]> arr[k] : arr[k-gap],arr[k] = arr[k],arr[k-gap] k -= 1 écart //= 2 # pilote pour vérifier le code arr2 = [12, 34, 54, 2, 3] print('input array:',arr2) shellSort(arr2) print('sorted array', arr2)>

input array: [12, 34, 54, 2, 3] sorted array [2, 3, 12, 34, 54]>

Complexité temporelle : Sur²).