Donné un BST , la tâche consiste à rechercher un nœud dans ce BST .

Pour rechercher une valeur dans BST, considérez-la comme un tableau trié. Nous pouvons maintenant facilement effectuer une opération de recherche dans BST en utilisant Algorithme de recherche binaire .

Algorithme pour rechercher une clé dans un arbre de recherche binaire donné :

Disons que nous voulons rechercher le numéro X, Nous commençons par la racine. Alors:

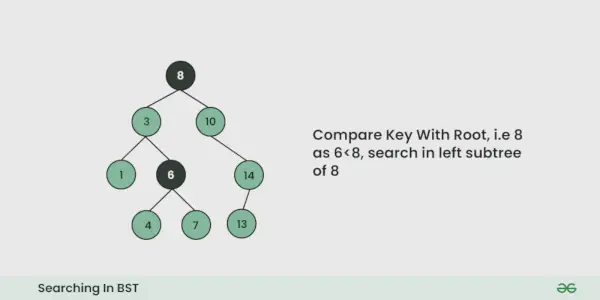
• On compare la valeur à rechercher avec la valeur de la racine.
  • Si c'est égal, nous avons terminé la recherche, si c'est plus petit, nous savons que nous devons aller au sous-arbre de gauche car dans un arbre de recherche binaire, tous les éléments du sous-arbre de gauche sont plus petits et tous les éléments du sous-arbre de droite sont plus grands.
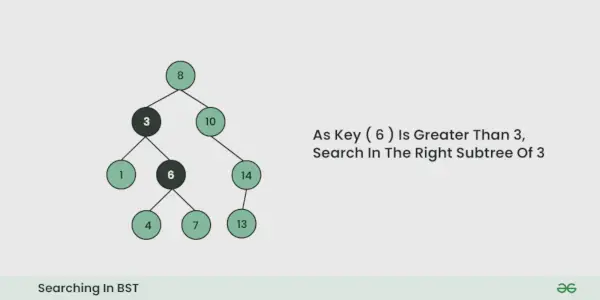
• Répétez l'étape ci-dessus jusqu'à ce qu'il n'y ait plus de traversée possible
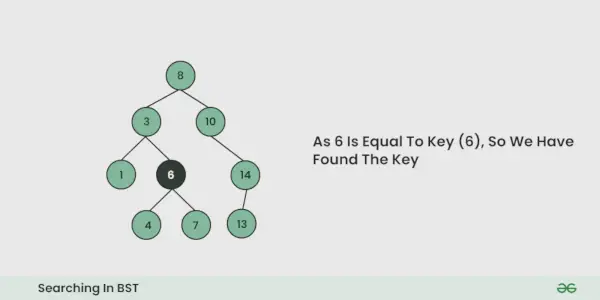
• Si à une itération, la clé est trouvée, retournez True. Sinon faux.

Illustration d'une recherche dans un BST :

Voir l'illustration ci-dessous pour une meilleure compréhension :

apurva padgaonkar

Programme pour implémenter la recherche dans BST :

C++

>

>

C

centos contre rhel

>

>

Java

>

>

Python3

algorithme de tri par insertion

>

>

C#

conversion de date en chaîne

> 
    
RJ12 contre RJ11
   
 
     
  
 
    
 
     
     
    
 
 
 
 
 
 // Javascript function to search a given key in a given BST> class Node {> >constructor(key) {> >this>.key = key;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // A utility function to insert> // a new node with given key in BST> function> insert(node, key) {> >// If the tree is empty, return a new node> >if> (node ===>null>) {> >return> new> Node(key);> >}> >// Otherwise, recur down the tree> >if> (key   node.left = insert(node.left, key);  } else if (key>node.key) { node.right = insert(node.right, clé);  } // Renvoie le pointeur de nœud (inchangé) return node; } // Fonction utilitaire pour rechercher une clé dans une fonction BST search(root, key) { // Cas de base : la racine est nulle ou la clé est présente à la racine if (root === null || root.key === key ) { retourner la racine ;  } // La clé est supérieure à la clé de root if (root.key return search(root.right, key); } // La clé est plus petite que la clé de root return search(root.left, key); } // Code du pilote let root = null; insert(root, 50); insert(root, 20); 60); insert(root, 80); // Clé à trouver let key = 6; // Recherche dans un BST if (search(root, key) === null) { console.log(key + ' not found'); } else { console.log(key + ' found'); } key = 60; // Recherche dans un BST if (search(root, key) === null) { console.log( clé + 'introuvable'); } else { console.log(clé + 'trouvé' }>'>);
 
 
 
 
    
 
> 
    
 6 not found 60 found>
 
    Complexité temporelle :    O(h), où h est la hauteur du BST.  
    Espace auxiliaire :    O(h), où h est la hauteur du BST. En effet, la quantité maximale d'espace nécessaire pour stocker la pile de récursion serait    h    .
 
    Liens connexes:     
 
 
  Opération d'insertion d'arbre de recherche binaire  
 
 Opération de suppression de l'arbre de recherche binaire