La programmation dynamique est une technique qui divise les problèmes en sous-problèmes et enregistre le résultat pour des usages futurs afin que nous n'ayons pas besoin de recalculer le résultat. Les sous-problèmes sont optimisés pour optimiser la solution globale, connue sous le nom de propriété de sous-structure optimale. L’utilisation principale de la programmation dynamique est de résoudre des problèmes d’optimisation. Ici, les problèmes d'optimisation signifient que lorsque nous essayons de trouver la solution minimale ou maximale d'un problème. La programmation dynamique garantit de trouver la solution optimale d'un problème si la solution existe.

La définition de la programmation dynamique indique qu'il s'agit d'une technique permettant de résoudre un problème complexe en divisant d'abord un ensemble de sous-problèmes plus simples, en résolvant chaque sous-problème une seule fois, puis en stockant leurs solutions pour éviter les calculs répétitifs.

Comprenons cette approche à travers un exemple.

Prenons un exemple de la série de Fibonacci. La série suivante est la série de Fibonacci :

comment désactiver le mode développeur sur Android

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…

Les nombres de la série ci-dessus ne sont pas calculés au hasard. Mathématiquement, nous pourrions écrire chacun des termes en utilisant la formule ci-dessous :

F(n) = F(n-1) + F(n-2),

Avec les valeurs de base F(0) = 0 et F(1) = 1. Pour calculer les autres nombres, nous suivons la relation ci-dessus. Par exemple, F(2) est la somme f(0) et f(1), qui est égal à 1.

Comment pouvons-nous calculer F(20) ?

Le terme F(20) sera calculé à l'aide de la nième formule de la série de Fibonacci. La figure ci-dessous montre comment F (20) est calculé.

algèbre relationnelle dans rdbms

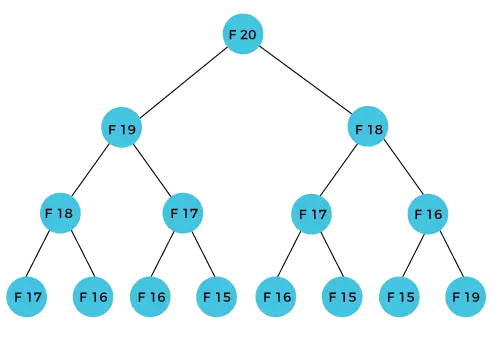
Comme nous pouvons le constater dans la figure ci-dessus, F(20) est calculé comme la somme de F(19) et F(18). Dans l’approche de programmation dynamique, nous essayons de diviser le problème en sous-problèmes similaires. Nous suivons cette approche dans le cas ci-dessus où F(20) dans les sous-problèmes similaires, c'est-à-dire F(19) et F(18). Si nous récapitulons la définition de la programmation dynamique, elle indique qu'un sous-problème similaire ne doit pas être calculé plus d'une fois. Néanmoins, dans le cas ci-dessus, le sous-problème est calculé deux fois. Dans l'exemple ci-dessus, F(18) est calculé deux fois ; de même, F(17) est également calculé deux fois. Cependant, cette technique est très utile car elle résout les sous-problèmes similaires, mais nous devons être prudents lors du stockage des résultats car nous ne sommes pas particulièrement soucieux de stocker le résultat que nous avons calculé une fois, cela peut alors entraîner un gaspillage de ressources.

Dans l'exemple ci-dessus, si nous calculons le F(18) dans le sous-arbre de droite, cela entraîne une énorme utilisation des ressources et diminue les performances globales.

La solution au problème ci-dessus consiste à enregistrer les résultats calculés dans un tableau. Tout d’abord, nous calculons F(16) et F(17) et enregistrons leurs valeurs dans un tableau. Le F(18) est calculé en additionnant les valeurs de F(17) et F(16), qui sont déjà enregistrées dans un tableau. La valeur calculée de F(18) est enregistrée dans un tableau. La valeur de F(19) est calculée en utilisant la somme de F(18) et F(17), et leurs valeurs sont déjà enregistrées dans un tableau. La valeur calculée de F(19) est stockée dans un tableau. La valeur de F(20) peut être calculée en additionnant les valeurs de F(19) et F(18), et les valeurs de F(19) et F(18) sont stockées dans un tableau. La valeur finale calculée de F(20) est stockée dans un tableau.

Comment fonctionne l’approche de programmation dynamique ?

Voici les étapes suivies par la programmation dynamique :

• Il décompose le problème complexe en sous-problèmes plus simples.
• Il trouve la solution optimale à ces sous-problèmes.
• Il stocke les résultats des sous-problèmes (mémorisation). Le processus de stockage des résultats des sous-problèmes est appelé mémorisation.
• Il les réutilise afin que le même sous-problème soit calculé plusieurs fois.
• Enfin, calculez le résultat du problème complexe.

Les cinq étapes ci-dessus constituent les étapes de base de la programmation dynamique. La programmation dynamique est applicable et possède des propriétés telles que :

Madhuri a dit

Ces problèmes qui ont des sous-problèmes qui se chevauchent et des sous-structures optimales. Ici, la sous-structure optimale signifie que la solution des problèmes d’optimisation peut être obtenue en combinant simplement la solution optimale de tous les sous-problèmes.

Dans le cas d’une programmation dynamique, la complexité spatiale augmenterait à mesure que nous stockons les résultats intermédiaires, mais la complexité temporelle diminuerait.

Approches de programmation dynamique

Il existe deux approches de la programmation dynamique :

• Approche descendante
• Une approche en profondeur

Approche descendante

L'approche descendante suit la technique de mémorisation, tandis que l'approche ascendante suit la méthode de tabulation. Ici, la mémorisation est égale à la somme de la récursivité et de la mise en cache. La récursion signifie appeler la fonction elle-même, tandis que la mise en cache signifie stocker les résultats intermédiaires.

Avantages

Mark Zuckerberg éducation

• C’est très simple à comprendre et à mettre en œuvre.
• Il résout les sous-problèmes uniquement lorsque cela est nécessaire.
• Il est facile de déboguer.

Désavantages

Il utilise la technique de récursion qui occupe plus de mémoire dans la pile d'appels. Parfois, lorsque la récursion est trop profonde, une condition de débordement de pile se produit.

Il occupe plus de mémoire, ce qui dégrade les performances globales.

Comprenons la programmation dynamique à travers un exemple.

 int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of &apos;n&apos; increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td>  </tr><tr><td>Bottom-Up</td>  </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let&apos;s understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let&apos;s understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>