Un ensemble en programmation Python est un type de données de collection non ordonné qui est itérable, mutable et ne comporte aucun élément en double.
L'ensemble est représenté par { } (valeurs entre accolades)
L'avantage majeur d'utiliser un ensemble, par opposition à un liste , c'est qu'il dispose d'une méthode hautement optimisée pour vérifier si un élément spécifique est contenu dans l'ensemble. Ceci est basé sur une structure de données appelée table de hachage. Puisque les ensembles ne sont pas ordonnés, nous ne pouvons pas accéder aux éléments à l’aide d’index comme nous le faisons dans les listes.
Exemple d'ensembles Python
Python3
var>=> {>'Geeks'>,>'for'>,>'Geeks'>}> type>(var)> |
>
>
cpld contre fpga
Sortir:
set>
Complexité temporelle : O(1)
Espace auxiliaire : O(1)
Casting de type avec la méthode Python Set
La méthode Python set() est utilisée pour le transtypage.
Python3
# typecasting list to set> myset>=> set>([>'a'>,>'b'>,>'c'>])> print>(myset)> # Adding element to the set> myset.add(>'d'>)> print>(myset)> |
>
>
Sortir:
L'ensemble Python est un type de données non ordonné, ce qui signifie que nous ne pouvons pas savoir dans quel ordre les éléments de l'ensemble sont stockés.
{'c', 'b', 'a'} {'d', 'c', 'b', 'a'}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Vérifiez unique et immuable avec Python Set
Les ensembles Python ne peuvent pas avoir de valeur en double et une fois créés, nous ne pouvons pas modifier sa valeur.
Python3
# Python program to demonstrate that> # a set cannot have duplicate values> # and we cannot change its items> # a set cannot have duplicate values> myset>=> {>'Geeks'>,>'for'>,>'Geeks'>}> print>(myset)> # values of a set cannot be changed> myset[>1>]>=> 'Hello'> print>(myset)> |
>
>
Sortir:
Le premier code explique que l'ensemble ne peut pas avoir de valeur en double. Chaque élément qu'il contient est une valeur unique.
Le deuxième code génère une erreur car nous ne pouvons pas attribuer ou modifier une valeur une fois l'ensemble créé. Nous pouvons uniquement ajouter ou supprimer des éléments dans l'ensemble.
{'Geeks', 'for'} TypeError: 'set' object does not support item assignment> Élément hétérogène avec ensemble Python
Les ensembles Python peuvent y stocker des éléments hétérogènes, c'est-à-dire qu'un ensemble peut stocker un mélange de types de données chaîne, entier, booléen, etc.
Python3
code gris
# Python example demonstrate that a set> # can store heterogeneous elements> myset>=> {>'Geeks'>,>'for'>,>10>,>52.7>,>True>}> print>(myset)> |
>
>
Sortir:
{True, 10, 'Geeks', 52.7, 'for'}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Ensembles gelés Python
Ensembles congelés en Python, ce sont des objets immuables qui ne prennent en charge que les méthodes et les opérateurs qui produisent un résultat sans affecter le ou les ensembles gelés auxquels ils sont appliqués. Cela peut être fait avec la méthode Frozenset() en Python.
Alors que les éléments d'un ensemble peuvent être modifiés à tout moment, les éléments de l'ensemble figé restent les mêmes après la création.
Si aucun paramètre n'est transmis, il renvoie un jeu gelé vide.
Python
# Python program to demonstrate differences> # between normal and frozen set> # Same as {'a', 'b','c'}> normal_set>=> set>([>'a'>,>'b'>,>'c'>])> print>(>'Normal Set'>)> print>(normal_set)> # A frozen set> frozen_set>=> frozenset>([>'e'>,>'f'>,>'g'>])> print>(>'
Frozen Set'>)> print>(frozen_set)> # Uncommenting below line would cause error as> # we are trying to add element to a frozen set> # frozen_set.add('h')> |
>
>
Sortir:
Normal Set {'a', 'c', 'b'} Frozen Set {'e', 'g', 'f'}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Fonctionnement interne de Set
Ceci est basé sur une structure de données appelée table de hachage. Si plusieurs valeurs sont présentes à la même position d'index, la valeur est ajoutée à cette position d'index pour former une liste chaînée.
Dans, les ensembles Python sont implémentés à l'aide d'un dictionnaire avec des variables factices, où la clé est l'ensemble des membres avec de plus grandes optimisations de la complexité temporelle.
Définir la mise en œuvre :
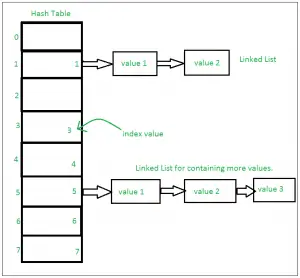
Ensembles avec de nombreuses opérations sur une seule HashTable :
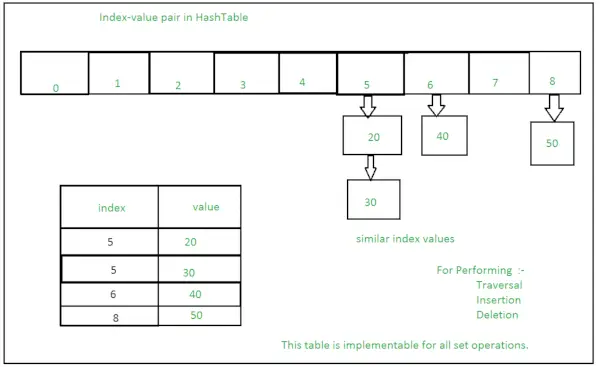
Méthodes pour les ensembles
Ajout d'éléments aux ensembles Python
L'insertion dans l'ensemble se fait à travers le set.add( ), où une valeur d'enregistrement appropriée est créée pour être stockée dans la table de hachage. Identique à la recherche d'un élément, c'est-à-dire O (1) en moyenne. Cependant, dans le pire des cas, cela peut devenir Sur) .
Python3
recherche contradictoire
# A Python program to> # demonstrate adding elements> # in a set> # Creating a Set> people>=> {>'Jay'>,>'Idrish'>,>'Archi'>}> print>(>'People:'>, end>=> ' '>)> print>(people)> # This will add Daxit> # in the set> people.add(>'Daxit'>)> # Adding elements to the> # set using iterator> for> i>in> range>(>1>,>6>):> >people.add(i)> print>(>'
Set after adding element:'>, end>=> ' '>)> print>(people)> |
>
>
Sortir:
People: {'Idrish', 'Archi', 'Jay'} Set after adding element: {1, 2, 3, 4, 5, 'Idrish', 'Archi', 'Jay', 'Daxit'}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Opération d'union sur les ensembles Python
Deux ensembles peuvent être fusionnés à l'aide de la fonction union() ou | opérateur. Les deux valeurs de la table de hachage sont accessibles et parcourues avec une opération de fusion effectuée sur elles pour combiner les éléments, en même temps les doublons sont supprimés. La complexité temporelle de ceci est O(len(s1) + len(s2)) où s1 et s2 sont deux ensembles dont l’union doit être effectuée.
Python3
# Python Program to> # demonstrate union of> # two sets> people>=> {>'Jay'>,>'Idrish'>,>'Archil'>}> vampires>=> {>'Karan'>,>'Arjun'>}> dracula>=> {>'Deepanshu'>,>'Raju'>}> # Union using union()> # function> population>=> people.union(vampires)> print>(>'Union using union() function'>)> print>(population)> # Union using '|'> # operator> population>=> people|dracula> print>(>'
Union using '|' operator'>)> print>(population)> |
>
souligner le texte avec CSS
>
Sortir:
Union using union() function {'Karan', 'Idrish', 'Jay', 'Arjun', 'Archil'} Union using '|' operator {'Deepanshu', 'Idrish', 'Jay', 'Raju', 'Archil'}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Opération d'intersection sur les ensembles Python
Cela peut être fait via l'opérateur intersection() ou &. Les éléments communs sont sélectionnés. Ils sont similaires à l'itération sur les listes de hachage et combinent les mêmes valeurs sur les deux tables. La complexité temporelle de ceci est O(min(len(s1), len(s2)) où s1 et s2 sont deux ensembles dont l'union doit être effectuée.
Python3
# Python program to> # demonstrate intersection> # of two sets> set1>=> set>()> set2>=> set>()> for> i>in> range>(>5>):> >set1.add(i)> for> i>in> range>(>3>,>9>):> >set2.add(i)> # Intersection using> # intersection() function> set3>=> set1.intersection(set2)> print>(>'Intersection using intersection() function'>)> print>(set3)> # Intersection using> # '&' operator> set3>=> set1 & set2> print>(>'
Intersection using '&' operator'>)> print>(set3)> |
>
>
Sortir:
Intersection using intersection() function {3, 4} Intersection using '&' operator {3, 4}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Trouver des différences d'ensembles en Python
Trouver des différences entre les ensembles. Semblable à la recherche de différences dans la liste chaînée. Cela se fait via l’opérateur différence() ou –. La complexité temporelle pour trouver la différence s1 – s2 est O(len(s1))
Python3
comment transformer une chaîne en entier
# Python program to> # demonstrate difference> # of two sets> set1>=> set>()> set2>=> set>()> for> i>in> range>(>5>):> >set1.add(i)> for> i>in> range>(>3>,>9>):> >set2.add(i)> # Difference of two sets> # using difference() function> set3>=> set1.difference(set2)> print>(>' Difference of two sets using difference() function'>)> print>(set3)> # Difference of two sets> # using '-' operator> set3>=> set1>-> set2> print>(>'
Difference of two sets using '-' operator'>)> print>(set3)> |
>
>
Sortir:
Difference of two sets using difference() function {0, 1, 2} Difference of two sets using '-' operator {0, 1, 2}> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Effacement des ensembles Python
La méthode Set Clear() vide l’ensemble de l’ensemble sur place.
Python3
# Python program to> # demonstrate clearing> # of set> set1>=> {>1>,>2>,>3>,>4>,>5>,>6>}> print>(>'Initial set'>)> print>(set1)> # This method will remove> # all the elements of the set> set1.clear()> print>(>'
Set after using clear() function'>)> print>(set1)> |
>
>
Sortir:
Initial set {1, 2, 3, 4, 5, 6} Set after using clear() function set()> Complexité temporelle : O(n)
Espace auxiliaire : O(n)
Cependant, il existe deux pièges majeurs dans les ensembles Python :
- L’ensemble ne conserve pas les éléments dans un ordre particulier.
- Seules les instances de types immuables peuvent être ajoutées à un ensemble Python.
Complexité temporelle des ensembles
| Opération | Cas moyen | Pire cas | Remarques |
|---|---|---|---|
| x en s | O(1) | Sur) | |
| Union merde | O(len(s)+len(t)) | ||
| S&T aux intersections | O(min(len(s), len(t)) | O(len(s) * len(t)) | remplacer min par max si t n'est pas un ensemble |
| Intersections multiples s1&s2&..&sn | (n-1)*O(l) où l est max(len(s1),..,len(sn)) | ||
| Différence merde | O(seulement(s)) |
Opérateurs pour les ensembles
Les ensembles et les ensembles figés prennent en charge les opérateurs suivants :
| Les opérateurs | Remarques |
|---|---|
| saisir s | contrôle de confinement |
| clé pas dans s | contrôle de non-confinement |
| s1 == s2 | s1 est équivalent à s2 |
| s1 != s2 | s1 n'est pas équivalent à s2 |
| s1 <= s2 | s1 est un sous-ensemble de s2 |
| s1 | s1 est un sous-ensemble approprié de s2 |
| s1>= s2 | s1 est un surensemble de s2 |
| s1> s2 | s1 est un sur-ensemble approprié de s2 |
| s1 | s2 | l'union de s1 et s2 |
| s1 et s2 | l'intersection de s1 et s2 |
| s1 – s2 | l'ensemble des éléments dans s1 mais pas dans s2 |
| s1 ˆ s2 | l'ensemble des éléments dans précisément l'un de s1 ou s2 |
Articles récents sur Python Set.
