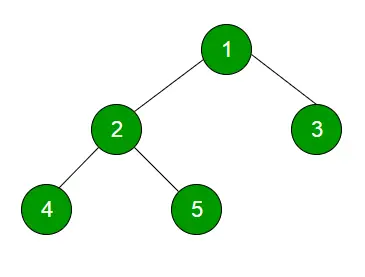
Traversée de l'ordre des niveaux La technique est définie comme une méthode pour parcourir un arbre de telle sorte que tous les nœuds présents dans le même niveau soient complètement parcourus avant de traverser le niveau suivant.

Exemple:
Traversée des ordres du niveau de pratique recommandé Essayez-le !Saisir:
Sortir:
1
23
Quatre cinq
Comment fonctionne le parcours d'ordre de niveau ?
L'idée principale du parcours par ordre de niveau est de parcourir tous les nœuds d'un niveau inférieur avant de passer à l'un des nœuds d'un niveau supérieur. Cela peut être fait de l'une des manières suivantes :
- le naïf (trouver la hauteur de l'arbre et parcourir chaque niveau et imprimer les nœuds de ce niveau)
- efficacement en utilisant une file d’attente.
Traversée d’ordre de niveau (approche naïve) :
Trouver hauteur d'arbre. Ensuite, pour chaque niveau, exécutez une fonction récursive en conservant la hauteur actuelle. Chaque fois que le niveau d'un nœud correspond, imprimez ce nœud.
Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus :
C++ // Recursive CPP program for level // order traversal of Binary Tree #include using namespace std; // A binary tree node has data, // pointer to left child // and a pointer to right child class node { public: int data; node *left, *right; }; // Function prototypes void printCurrentLevel(node* root, int level); int height(node* node); node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(node* root, int level) { if (root == NULL) return; if (level == 1) cout << root->données<< ' '; else if (level>1) { printCurrentLevel(root->gauche, niveau - 1); printCurrentLevel(racine->droite, niveau - 1); } } // Calcule la 'hauteur' d'un arbre -- le nombre de // nœuds le long du chemin le plus long depuis le nœud racine // jusqu'au nœud feuille le plus éloigné. int height(node* node) { if (node == NULL) return 0; else { // Calcule la hauteur de chaque sous-arbre int lheight = height(node->left); int rheight = hauteur(nœud->droite); // Utilisez le plus grand if (lheight> rheight) { return (lheight + 1); } else { return (hauteur + 1); } } } // Fonction d'assistance qui alloue // un nouveau nœud avec les données données et // des pointeurs gauche et droit NULL. node* newNode(int data) { node* Node = new node(); Nœud->données = données ; Nœud->gauche = NULL ; Nœud->droite = NULL ; retourner (nœud); } // Code du pilote int main() { node* root = newNode(1); racine->gauche = newNode(2); racine->droite = newNode(3); racine->gauche->gauche = newNode(4); racine->gauche->droite = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; } // This code is contributed by rathbhupendra> C // Recursive C program for level // order traversal of Binary Tree #include #include // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node *left, *right; }; // Function prototypes void printCurrentLevel(struct node* root, int level); int height(struct node* node); struct node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(struct node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(struct node* root, int level) { if (root == NULL) return; if (level == 1) printf('%d ', root->données); else if (niveau> 1) { printCurrentLevel(root->left, niveau - 1); printCurrentLevel(racine->droite, niveau - 1); } } // Calcule la 'hauteur' d'un arbre -- le nombre de // nœuds le long du chemin le plus long depuis le nœud racine // jusqu'au nœud feuille le plus éloigné int height(struct node* node) { if (node == NULL) renvoie 0 ; else { // Calcule la hauteur de chaque sous-arbre int lheight = height(node->left); int rheight = hauteur(nœud->droite); // Utilisez le plus grand if (lheight> rheight) return (lheight + 1); sinon return (hauteur + 1); } } // Fonction d'assistance qui alloue un nouveau nœud avec les données // données et les pointeurs gauche et droit NULL. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); nœud->données = données ; nœud->gauche = NULL ; nœud->droite = NULL ; return (nœud); } // Programme pilote pour tester les fonctions ci-dessus int main() { struct node* root = newNode(1); racine->gauche = newNode(2); racine->droite = newNode(3); racine->gauche->gauche = newNode(4); racine->gauche->droite = newNode(5); printf('Le parcours de l'ordre de niveau de l'arbre binaire est
'); printLevelOrder(racine); renvoie 0 ; }> Java // Recursive Java program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class BinaryTree { // Root of the Binary Tree Node root; public BinaryTree() { root = null; } // Function to print level order traversal of tree void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number of // nodes along the longest path from the root node // down to the farthest leaf node. int height(Node root) { if (root == null) return 0; else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rhauteur) retour (lhauteur + 1); sinon return (hauteur + 1); } } // Imprimer les nœuds au niveau actuel void printCurrentLevel(Node root, int level) { if (root == null) return; if (level == 1) System.out.print(root.data + ' '); sinon if (niveau> 1) { printCurrentLevel(root.left, niveau - 1); printCurrentLevel(root.right, niveau - 1); } } // Programme pilote pour tester les fonctions ci-dessus public static void main(String args[]) { BinaryTree tree = new BinaryTree(); arbre.root = nouveau Node(1); arbre.root.left = new Node(2); arbre.root.right = new Node(3); arbre.root.left.left = new Node(4); arbre.root.left.right = new Node(5); System.out.println('Le parcours de l'ordre de niveau de' + 'l'arbre binaire est '); arbre.printLevelOrder(); } }> Python # Recursive Python program for level # order traversal of Binary Tree # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Function to print level order traversal of tree def printLevelOrder(root): h = height(root) for i in range(1, h+1): printCurrentLevel(root, i) # Print nodes at a current level def printCurrentLevel(root, level): if root is None: return if level == 1: print(root.data, end=' ') elif level>1: printCurrentLevel(root.left, level-1) printCurrentLevel(root.right, level-1) # Calcule la hauteur d'un arbre - le nombre de nœuds # le long du chemin le plus long depuis le nœud racine jusqu'à # la feuille la plus éloignée node def height(node) : si node est None : renvoie 0 sinon : # Calcule la hauteur de chaque sous-arbre lheight = height(node.left) rheight = height(node.right) # Utilisez le plus grand si lheight> rheight : return lheight+1 else : return rheight+1 # Programme pilote pour tester la fonction ci-dessus si __name__ == '__main__' : root = Node(1) root.left = Node(2) root.right = Node(3) root. left.left = Node(4) root.left.right = Node(5) print('Le parcours d'ordre de niveau de l'arbre binaire est -') printLevelOrder(root) # Ce code est contribué par Nikhil Kumar Singh(nickzuck_007)> C# // Recursive c# program for level // order traversal of Binary Tree using System; // Class containing left and right // child of current node and key value public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { // Root of the Binary Tree public Node root; public void BinaryTree() { root = null; } // Function to print level order // traversal of tree public virtual void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) { printCurrentLevel(root, i); } } // Compute the 'height' of a tree -- // the number of nodes along the longest // path from the root node down to the // farthest leaf node. public virtual int height(Node root) { if (root == null) { return 0; } else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rhauteur) { return (lhauteur + 1); } else { return (hauteur + 1); } } } // Imprimer les nœuds au niveau actuel public virtual void printCurrentLevel(Node root, int level) { if (root == null) { return; } if (niveau == 1) { Console.Write(root.data + ' '); } else if (niveau> 1) { printCurrentLevel(root.left, niveau - 1); printCurrentLevel(root.right, niveau - 1); } } // Code du pilote public static void Main(string[] args) { GFG tree = new GFG(); arbre.root = nouveau Node(1); arbre.root.left = new Node(2); arbre.root.right = new Node(3); arbre.root.left.left = new Node(4); arbre.root.left.right = new Node(5); Console.WriteLine('Le parcours d'ordre de niveau ' + 'de l'arbre binaire est '); arbre.printLevelOrder(); } } // Ce code est contribué par Shrikant13> Javascript // Recursive javascript program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Root of the Binary Tree var root= null; // Function to print level order traversal of tree function printLevelOrder() { var h = height(root); var i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number // of nodes along the longest path // from the root node down to the farthest leaf node. function height(root) { if (root == null) return 0; else { // Compute height of each subtree var lheight = height(root.left); var rheight = height(root.right); // Use the larger one if (lheight>rhauteur) retour (lhauteur + 1); sinon return (hauteur + 1); } } // Imprimer les nœuds au niveau actuel function printCurrentLevel(root , level) { if (root == null) return; if (level == 1) console.log(root.data + ' '); sinon if (niveau> 1) { printCurrentLevel(root.left, niveau - 1); printCurrentLevel(root.right, niveau - 1); } } // Programme pilote pour tester les fonctions ci-dessus root = new Node(1); root.left = nouveau nœud (2); root.right = nouveau nœud (3); root.left.left = nouveau nœud (4); root.left.right = new Node(5); console.log('Le parcours d'ordre de niveau de l'arbre binaire est '); printLevelOrder(); // Ce code est contribué par umadevi9616> Sortir
Level Order traversal of binary tree is 1 2 3 4 5>
Complexité temporelle : O(N), où N est le nombre de nœuds dans l'arbre asymétrique.
Espace auxiliaire : O(1) Si la pile de récursion est considérée, l'espace utilisé est O(N).
liste de tableaux et liste de liens
Traversée de l'ordre de niveau à l'aide de File d'attente
Nous devons visiter les nœuds d'un niveau inférieur avant tout nœud d'un niveau supérieur, cette idée est assez similaire à celle d'une file d'attente. Poussez les nœuds d'un niveau inférieur dans la file d'attente. Lorsqu'un nœud est visité, supprimez ce nœud de la file d'attente et placez l'enfant de ce nœud dans la file d'attente.
Cela garantit que les nœuds d'un niveau inférieur sont visités avant tout nœud d'un niveau supérieur.
Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus :
C++ // C++ program to print level order traversal #include using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // Iterative method to find height of Binary Tree void printLevelOrder(Node* root) { // Base Case if (root == NULL) return; // Create an empty queue for level order traversal queueq; // Mettre la racine en file d'attente et initialiser la hauteur q.push(root); while (q.empty() == false) { // Imprimer le début de la file d'attente et le supprimer de la file d'attente Node* node = q.front(); cout<< node->données<< ' '; q.pop(); // Enqueue left child if (node->gauche != NULL) q.push(node->left); // Mettre en file d'attente l'enfant droit if (node->right != NULL) q.push(node->right); } } // Fonction utilitaire pour créer un nouveau nœud d'arborescence Node* newNode(int data) { Node* temp = new Node; temp->données = données ; temp->gauche = temp->droite = NULL ; température de retour ; } // Programme pilote pour tester les fonctions ci-dessus int main() { // Créons l'arbre binaire illustré dans le diagramme ci-dessus Node* root = newNode(1); racine->gauche = newNode(2); racine->droite = newNode(3); racine->gauche->gauche = newNode(4); racine->gauche->droite = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; }> C // Iterative Queue based C program // to do level order traversal // of Binary Tree #include #include #define MAX_Q_SIZE 500 // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node* left; struct node* right; }; // Function prototypes struct node** createQueue(int*, int*); void enQueue(struct node**, int*, struct node*); struct node* deQueue(struct node**, int*); // Given a binary tree, print its nodes in level order // using array for implementing queue void printLevelOrder(struct node* root) { int rear, front; struct node** queue = createQueue(&front, &rear); struct node* temp_node = root; while (temp_node) { printf('%d ', temp_node->données); // Mettre l'enfant gauche en file d'attente if (temp_node->left) enQueue(queue, &rear, temp_node->left); // Mettre en file d'attente l'enfant droit if (temp_node->right) enQueue(queue, &rear, temp_node->right); // Supprimez le nœud de la file d'attente et faites-en temp_node temp_node = deQueue(queue, &front); } } // Fonctions utilitaires struct node** createQueue(int* front, int* Rear) { struct node** queue = (struct node**)malloc( sizeof(struct node*) * MAX_Q_SIZE); *avant = *arrière = 0 ; file d'attente de retour ; } void enQueue(struct node** queue, int* arrière, struct node* new_node) { queue[*rear] = new_node; (*arrière)++ ; } struct node* deQueue(struct node** queue, int* front) { (*front)++; file d'attente de retour[*front - 1]; } // Fonction d'assistance qui alloue un nouveau nœud avec les données // données et les pointeurs gauche et droit NULL. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); nœud->données = données ; nœud->gauche = NULL ; nœud->droite = NULL ; return (nœud); } // Programme pilote pour tester les fonctions ci-dessus int main() { struct node* root = newNode(1); racine->gauche = newNode(2); racine->droite = newNode(3); racine->gauche->gauche = newNode(4); racine->gauche->droite = newNode(5); printf('Le parcours de l'ordre de niveau de l'arbre binaire est
'); printLevelOrder(racine); renvoie 0 ; }> Java // Iterative Queue based Java program // to do level order traversal // of Binary Tree import java.util.LinkedList; import java.util.Queue; // Class to represent Tree node class Node { int data; Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order // using array for implementing queue void printLevelOrder() { Queuefile d'attente = nouvelle LinkedList(); file d'attente.add(racine); while (!queue.isEmpty()) { // poll() supprime la tête actuelle. Nœud tempNode = queue.poll(); System.out.print(tempNode.data + ''); // Mettre l'enfant gauche en file d'attente if (tempNode.left != null) { queue.add(tempNode.left); } // Mettre l'enfant droit en file d'attente if (tempNode.right != null) { queue.add(tempNode.right); } } } public static void main(String args[]) { // Création d'un arbre binaire et saisie // des nœuds BinaryTree tree_level = new BinaryTree(); tree_level.root = nouveau nœud (1); tree_level.root.left = new Node(2); tree_level.root.right = new Node(3); tree_level.root.left.left = new Node(4); tree_level.root.left.right = new Node(5); System.out.println('Le parcours d'ordre de niveau de l'arbre binaire est - '); tree_level.printLevelOrder(); } }> Python # Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Imprimer le début de la file d'attente et # le supprimer de la file d'attente print(queue[0].data, end=' ') node = queue.pop(0) # Mettre l'enfant gauche en file d'attente si node.left n'est pas Aucun : queue.append(node.left) # Mettre l'enfant droit en file d'attente si node.right n'est pas Aucun : queue.append(node.right) # Programme pilote pour tester la fonction ci-dessus si __name__ == '__main__' : root = Node(1 ) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Le parcours d'ordre de niveau de l'arbre binaire est - ') printLevelOrder(root) # Ce code est contribué par Nikhil Kumar Singh(nickzuck_007)> C# // Iterative Queue based C# program // to do level order traversal // of Binary Tree using System; using System.Collections.Generic; // Class to represent Tree node public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal public class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order using // array for implementing queue void printLevelOrder() { Queuefile d'attente = nouvelle file d'attente(); queue.Enqueue(racine); while (queue.Count != 0) { Node tempNode = queue.Dequeue(); Console.Write(tempNode.data + ''); // Mettre en file d'attente l'enfant gauche if (tempNode.left != null) { queue.Enqueue(tempNode.left); } // Mettre l'enfant droit en file d'attente if (tempNode.right != null) { queue.Enqueue(tempNode.right); } } } // Code du pilote public static void Main() { // Création d'un arbre binaire et saisie // des nœuds BinaryTree tree_level = new BinaryTree(); tree_level.root = nouveau nœud (1); tree_level.root.left = new Node(2); tree_level.root.right = new Node(3); tree_level.root.left.left = new Node(4); tree_level.root.left.right = new Node(5); Console.WriteLine('Le parcours d'ordre de niveau ' + 'de l'arbre binaire est - '); tree_level.printLevelOrder(); } } // Ce code a été contribué par PrinciRaj1992> Javascript class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Class to represent a deque (double-ended queue) class Deque { constructor() { this.queue = []; } // Method to add an element to the end of the queue enqueue(item) { this.queue.push(item); } // Method to remove and return the first element of the queue dequeue() { return this.queue.shift(); } // Method to check if the queue is empty isEmpty() { return this.queue.length === 0; } } // Function to perform level order traversal of a binary tree function printLevelOrder(root) { // Create a deque to store nodes for traversal const queue = new Deque(); // Add the root node to the queue queue.enqueue(root); // Continue traversal until the queue is empty while (!queue.isEmpty()) { // Remove and get the first node from the queue const tempNode = queue.dequeue(); // Print the data of the current node console.log(tempNode.data + ' '); // Enqueue the left child if it exists if (tempNode.left !== null) { queue.enqueue(tempNode.left); } // Enqueue the right child if it exists if (tempNode.right !== null) { queue.enqueue(tempNode.right); } } } // Create a binary tree and enter the nodes const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); // Print the level order traversal of the binary tree console.log('Level order traversal of binary tree is - '); printLevelOrder(root);> Sortir
Level Order traversal of binary tree is 1 2 3 4 5>
Complexité temporelle : O(N) où N est le nombre de nœuds dans l'arbre binaire.
Espace auxiliaire : O(N) où N est le nombre de nœuds dans l'arbre binaire.