UN Fonction en mathématiques, il s'agit d'une relation spéciale entre l'ensemble des valeurs d'entrée et l'ensemble des valeurs de sortie. Dans Function, chaque valeur d’entrée donne une valeur de sortie particulière. Nous représentons une fonction en mathématiques comme, y = f(x) où X est la valeur d'entrée et pour chaque X nous obtenons une valeur de sortie comme y.

Dans cet article, nous découvrirons, fonctions en mathématiques, leurs différents types, exemples et autres en détail.

Table des matières

• Qu’est-ce qu’une fonction en mathématiques ?
• Définition de fonction en mathématiques
• Exemples de fonctions
• Condition pour une fonction
• Représentation des fonctions en mathématiques
• Identification de la fonction
• Types de fonctions
• Qu’est-ce qu’une fonction en algèbre ?
• Domaine et étendue d'une fonction
• Composition des fonctions
• Algèbre des fonctions
• Qu'est-ce qu'une fonction sur un graphique ?
• Fonctions graphiques
• Fonctions communes
• Applications des fonctions
• Exemples sur la fonction
• Problèmes pratiques sur ce qu'est une fonction

Qu’est-ce qu’une fonction en mathématiques ?

Une fonction en mathématiques est une relation entre les valeurs d'entrée (domaine) et les valeurs de sortie (plage) des ensembles donnés de telle sorte qu'aucune variable des ensembles de domaines ne soit liée à la même variable dans l'ensemble de plages. Un exemple simple de fonction en mathématiques est f(x) = 2x, qui est défini sur R→R, ici toute variable du domaine est liée à une seule variable de la plage.

Une fonction en mathématiques a un domaine, un codomaine et une plage. Le domaine est l'ensemble de toutes les valeurs possibles de x et la plage de la fonction est l'ensemble de toutes les valeurs de sortie de y. La plage est le sous-ensemble du codomaine d'une fonction. Nous pouvons également dire qu'une fonction en mathématiques est une relation avec une sortie unique et qu'aucune valeur d'entrée n'a une sortie similaire dans une fonction, ce qui est le cas pour la relation.

Définition de fonction en mathématiques

La fonction est une relation ou une méthode spéciale reliant chaque membre de l'ensemble A à un membre unique de l'ensemble B via une relation définie. L'ensemble A est appelé le domaine et l'ensemble B est appelé le co-domaine de la fonction. Une fonction en mathématiques de l'ensemble A à l'ensemble B est définie comme :

f = ∀ une ∈ UNE, b ∈ B

Chaque fonction est une relation mais toute relation n'est pas une fonction. Les critères pour que toute relation soit considérée comme une fonction car en fonction, chaque élément de l'ensemble A n'a qu'une seule image dans l'ensemble B tandis qu'en relation, un élément de l'ensemble A peut avoir plus d'une image dans l'ensemble B.

Nous définissons une fonction en mathématiques d'un ensemble non vide A à un ensemble non vide B tel que,

(a, b) ∈ f, alors f(a) = b

où nous avons appelé b comme l'image de un défini sous la relation F .

Chaque élément 'un' de l'ensemble A a une image unique ' b ‘ dans l’ensemble B alors c’est une fonction.

Exemples de fonctions

Une fonction en mathématiques f est définie comme y = f(x) où X est la valeur d'entrée, et pour chaque valeur d'entrée de x, nous obtenons une valeur unique de y. Divers exemples de fonctions mathématiques définies sur R → R sont,

• y = f(x) = 3x + 4
• y = f(x) = péché x + 3
• y = f(x) = -3x²+ 3, etc.

Condition pour une fonction

Pour deux ensembles non vides A et B, une fonction f : A → B dénote que F est une fonction de A vers B, où UN est un domaine et B est un co-domaine.

Pour tout élément, a ∈ A, un élément unique, b ∈ B est là tel que (a,b) ∈ f. L'élément unique b qui est lié à a est noté f(a) et se lit comme f de a. Cela peut être mieux compris à partir de l’image ci-dessous :

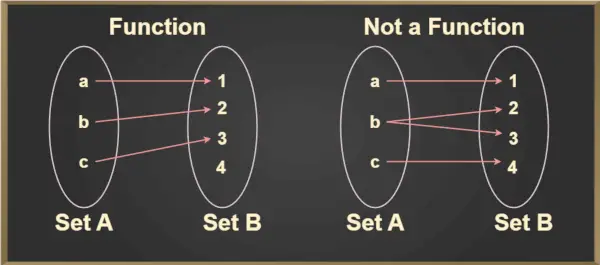
Test de ligne verticale

Le test de ligne verticale est utilisé pour déterminer si une courbe est une fonction ou non. Si une courbe coupe une ligne verticale en plus d’un point, alors la courbe n’est pas une fonction.

Représentation des fonctions en mathématiques

Nous représentons une fonction en mathématiques comme,

y = f(x) = x + 3

Ici, l'ensemble des valeurs de x est le domaine de la fonction et l'ensemble des valeurs de sortie de y est le co-domaine de la fonction. Ici, la fonction est définie pour tous les nombres réels car elle donne une valeur unique pour chaque x mais il n'est pas toujours possible d'obtenir le résultat pour chaque valeur de x dans ce cas nous définissons la fonction en deux parties, cela peut être compris comme

• f(x) = 1/(x – 2), où x ≠ 2
• f(x) = x²où x ∈ {R}

Nous pouvons définir une fonction en mathématiques comme une machine qui prend des entrées et donne une sortie unique. La fonction f(x) = x²est défini ci-dessous comme,

Nous pouvons représenter une fonction en mathématiques par la méthode des trois comme,

• Ensemble de paires ordonnées
• Formulaire de tableau
• Forme graphique

Par exemple, si nous représentons une fonction comme, f(x) = x³

Une autre façon de représenter la même fonction est de ensemble de paires ordonnées comme,

f = {(1,1), (2,8), (3,27)}

Dans l'ensemble mentionné ci-dessus, le domaine de la fonction est D = {1, 2, 3} et la plage de la fonction est R = {1, 8, 27}

Identification de la fonction

La fonction est classée comme un type spécial de relation en mathématiques. Il existe les règles suivantes qui peuvent être utilisées pour identifier une fonction :

• Une relation dans laquelle chaque entrée mappée à une sortie unique est une fonction. Cela s'appelle une fonction un à un.
• Une relation dans laquelle deux entrées (préimage) mappées sur une seule sortie est également une fonction. Il s’agit de plusieurs fonctions à une.
• Une relation dans laquelle une entrée correspond à deux sorties différentes n’est pas une fonction.
• Une relation dans laquelle de nombreuses entrées sont mappées à de nombreuses sorties sans suivre de règle spécifique n’est pas une fonction.

Types de fonctions

Différent Types de fonctions sont utilisés pour résoudre divers types de problèmes mathématiques, notamment liés aux courbes et aux équations. Il existe trois principaux types de fonctions en mathématiques qui sont basées sur le mappage d'éléments de l'ensemble A à l'ensemble B.

Fonction injective ou fonction One to One

La fonction dans laquelle chaque élément du domaine a une image distincte dans le codomaine est appelée la Injectif ou Fonction One-to-One .

f : A → B est dit biunivoque ou injectif si les images d'éléments distincts de A sous f sont distinctes, c'est-à-dire

FA ₁ ) = b ₁ , FA ₂ ) = b ₂

où un₁, un₂∈ A et b₁, b₂∈B

Fonctions surjectives ou sur fonction

La fonction surjective est la fonction dans laquelle chaque élément du codomaine a une pré-image dans le domaine. On l'appelle aussi Sur la fonction ce qui signifie que chaque élément du codomaine est associé à chaque élément du domaine. Aucun élément de codomaine ne doit avoir une relation vide. Le nombre d'éléments de codomaine et de plage est le même.

f : A → B est dit être sur, si chaque élément de B est l'image d'un élément de A sous f, c'est-à-dire que pour tout b ϵ B, il existe un élément 'a' dans A tel que f(a) = b.

Fonction bijective

Si une fonction a des propriétés à la fois Injective (One to One) et Surjective (Onto function), alors la fonction est appelée un Fonction bijective . Dans la fonction bijective, chaque élément du domaine est lié à chaque élément du codomaine et il existe également une relation bijective. Cela implique que le nombre d'éléments du codomaine et de la plage sont les mêmes et qu'aucun élément du domaine ou du codomaine n'a de relation vide.

Sur la base des valeurs de sortie, les fonctions sont classées comme fonctions paires et impaires. Jetons un coup d'oeil sur eux

Fonctions étranges

La fonction impaire est un type de fonction qui présente une symétrie par rapport à l'origine. Plus précisément, si f(x) est une fonction impaire, elle montre que f(-x) = -f(x)

Même fonction

La fonction paire est un type de fonction qui présente une symétrie par rapport à l’axe y. Plus précisément, si f(x) est une fonction paire, elle montre que f(-x) = f(x)

Qu’est-ce qu’une fonction en algèbre ?

Une fonction dans algèbre est une équation pour laquelle tout x pouvant être introduit dans l'équation produira exactement une sortie telle que y hors de l'équation. Il est représenté par y = f(x), où x est une variable indépendante et y est une variable dépendante.

Par exemple:

• y = 2x + 1
• y = 3x – 2
• y = 4a
• y = 5/x

Domaine et étendue d'une fonction

Domaine et plage d'une fonction sont respectivement la valeur d'entrée et de sortie d'une fonction. Par exemple, disons que nous avons une fonction donnée par f(x) = x². Ici, nous pouvons prendre tout le nombre réel comme valeur d’entrée de x et la sortie sera toujours un nombre réel positif. Par conséquent, son domaine est un ensemble de tous les nombres réels représentés par R tandis que sa plage est un ensemble de nombres réels positifs représentés par R.⁺

Composition des fonctions

Si f : A → B et g : B → C soient deux fonctions. Alors la composition de f et g est notée f(g) et elle est définie comme la fonction brouillard = f(g(x)) pour x ∈ A.

Prenons deux fonctions f(x) = x + 3 et g(x) = 2x²

brouillard = f(g(x))

⇒ brouillard = f(2x²)

⇒ dent = 2x²+ 3

Apprendre encore plus, Composition de la fonction

Algèbre des fonctions

L'algèbre des fonctions implique les opérations algébriques effectuées entre deux fonctions. Les opérations algébriques pour deux fonctions f(x) et g(x) définies sur la valeur réelle de x sont mentionnées ci-dessous :

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Car, k est un nombre réel}
• (f/g)(x) = f(x) /g(x); {Pour g(x) ≠ 0}

Qu'est-ce qu'une fonction sur un graphique ?

Une fonction peut être facilement représentée sur un graphique. Toute fonction sur le graphique représente une courbe (y compris une ligne droite) dans le plan xy mappé pour ses valeurs d'entrée et de sortie correspondantes.

Pour tracer une fonction sur un, recherchez d'abord quelques points qui se trouvent sur la fonction, puis joignez ces points en fonction du lieu de la fonction. Par exemple, pour représenter graphiquement la fonction (ligne droite) f(x) = y = 5x – 2, nous avons besoin d'un point sur le graphique. Pour trouver le point sur le graphique, nous prenons d'abord les valeurs aléatoires de x, puis trouvons leurs valeurs correspondantes de y, comme,

f(x) = y = 5x-2

si x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

si x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

si x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

En joignant maintenant ces points, nous pouvons obtenir le graphique de la fonction y = 5x – 2

Fonctions graphiques

Connaître les valeurs de x permet de représenter une fonction f(x) sur un graphique. Parce que y = f(x), nous pouvons trouver la valeur associée pour y en commençant par les valeurs de x. En conséquence, nous pouvons tracer un graphique dans un plan de coordonnées en utilisant les valeurs x et y. Considérez le scénario suivant :

Supposons que y = x + 3

Quand x = 0, y = 3

De la même manière,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

En conséquence, nous pouvons tracer le graphique de la fonction x + 3 en utilisant ces valeurs.

Fonctions communes

Certaines fonctions courantes couramment utilisées en mathématiques sont décrites ci-dessous :

Fonction réelle

Fonction réelle en mathématiques, fait référence à une fonction dont le domaine et l'étendue sont des sous-ensembles des nombres réels (notés ℝ). En termes plus simples, une fonction réelle est une règle ou une relation mathématique qui attribue une valeur numérique réelle à chaque entrée numérique.

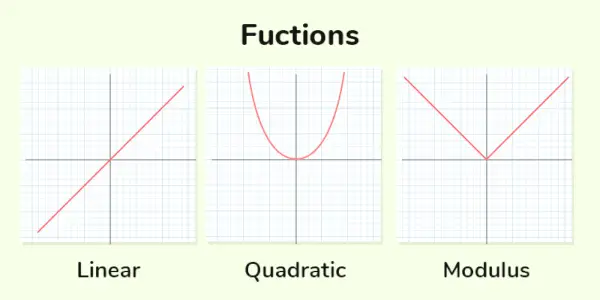
Fonctions réelles

Fonction polynomiale

La fonction dans laquelle les exposants des variables algébriques sont des entiers non négatifs est appelée une Fonction polynomiale . Si la puissance de la variable est 1, on parle de fonction linéaire, si la puissance est de 2, on parle de fonction quadratique et si la puissance est de 3, on parle de fonction cubique. Quelques exemples de fonctions polynomiales sont mentionnés ci-dessous :

• y = x²
• y = 2x + 3
• y = 3x³

La fonction polynomiale peut en outre être classée dans les types suivants :

Fonction linéaire : Les fonctions linéaires sont celles dans lesquelles la puissance maximale de la variable est de 1. La forme générale de Fonction linéaire est y = mx + c

Fonction quadratique : Les fonctions quadratiques sont celles dans lesquelles la puissance maximale de la variable est de 2. Forme générale de fonction quadratique est, hache ² + bx + c = 0

Fonction cubique : Fonction cubique sont ceux dans lesquels la puissance maximale de la variable est de 3. La forme générale de la fonction cubique est donnée comme hache ³ + boîte ² + cx + d = 0

Fonction inverse

Fonction inverse est la fonction contenant l'inverse d'une autre fonction. Disons que nous avons une fonction y = f(x) alors sa fonction inverse sera x = f^-1(o). Dans y = f(x), le domaine est x et la plage est y tandis que dans le cas de x = f^-1(y), le domaine est y et la plage est x. Ainsi, nous pouvons dire que le domaine de la fonction d'origine est l'étendue de sa fonction inverse et que l'étendue de la fonction d'origine est le domaine de la fonction d'origine. Quelques exemples de fonctions inverses sont,

• y = donc^-1(X)
• y = x^-1

Fonction de zone

La fonction de zone fait généralement référence à une fonction mathématique qui calcule la surface d'une forme ou d'une région géométrique. La fonction zone prend un ou plusieurs paramètres en entrée et renvoie la zone de la forme correspondante. Certaines des fonctions de la zone sont décrites ci-dessous :

Fonction de l'aire du cercle : Aire du cercle (A) est fonction de son rayon (r) tel que,

A = πr ²

Aire de fonction du triangle : Aire du Triangle (A) est fonction de sa base (b) et de sa hauteur (h) telles que,

A = (bh)/2

Fonction exponentielle

Fonction exponentielle est celui qui est représenté par f(x) = e^X. Il est souvent utilisé pour montrer une croissance ou une décroissance rapide.

Fonction logarithmique

Fonction logarithmique est une fonction mathématique qui représente l'opération inverse de l'exponentiation. Il est représenté par f(x) = log x.

Fonction de plafond

Fonction plafond , noté ⌈x⌉, arrondit un nombre réel x à l'entier le plus proche supérieur ou égal à x. En d’autres termes, il trouve la plus petite valeur entière supérieure ou égale à x.

Fonction du sol

La fonction Floor, notée ⌊x⌋, arrondit un nombre réel x à l'entier le plus proche inférieur ou égal à x. En d’autres termes, il trouve la plus grande valeur entière inférieure ou égale à x.

Fonction module

Fonction module , également connue sous le nom de fonction valeur absolue, renvoie la grandeur ou la taille d'un nombre réel sans tenir compte de son signe. La fonction module est notée ∣x∣, où x est la valeur d'entrée.

génération de nombres aléatoires java

Fonction Signum

Fonction Signum , également connue sous le nom de fonction signe ou fonction signum, est une fonction mathématique qui renvoie le signe d'un nombre réel. Il indique si le nombre est positif, négatif ou nul.

Fonctions trigonométriques

Fonctions trigonométriques sont des fonctions mathématiques qui relient les angles d'un triangle rectangle à la longueur de ses côtés. Les six fonctions trigonométriques principales sont le sinus (sin), le cosinus (cos), la tangente (tan), la cosécante (cosec), la sécante (sec) et la cotangente (cot).

Fonctions complexes

Toute fonction dans laquelle la variable d'entrée est une fonction complexe est appelée fonction complexe. Un nombre complexe est un nombre qui peut être tracé sur le plan complexe. Dans un nombre complexe nous avons un nombre réel et un nombre imaginaire. Un nombre complexe (z) est représenté par z= x + iy et une fonction complexe est représentée par f(z) = P(x, y) + iQ(x, y)

Applications des fonctions

Quand on dit qu’une quantité variable y est fonction d’une quantité variable x, on indique que y dépend de x et que la valeur de y est déterminée par la valeur de x. Cette dépendance peut s'exprimer comme suit : f = y (x).

• Le rayon d'un cercle peut être utilisé pour calculer l'aire d'un cercle. Le rayon r affecte la zone A. Nous déclarons que A est fonction de r dans le langage mathématique des fonctions. On peut écrire A = f(r) =π×r²
• Le volume V d’une sphère est fonction de son rayon. V = f(r) = 4/3×r³désigne la dépendance de V sur r.
• La force est fonction de l’accélération d’un corps de masse fixe m. F = g(une) = m×une.

Les gens lisent également :

• Relation et fonction
  
• Domaine et plage des fonctions trigonométriques
• Portée d'une fonction
• Fonction hyperbolique

Exemples sur la fonction

Exemple 1 : Pour deux fonctions, f et g sont définis comme suit : f(x) = x ² et g(x) = ln(2x). Trouver la fonction composite (gof )( x )

Solution:

Donné:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Ainsi, (gof)(x) = 2 ln(√2x)

Exemple 2 : Trouver la sortie de la fonction g(t)= 6t ² + 5 à

• (je) t = 0
• (ii) t = 2

Solution:

Fonction donnée,

g(t)= 6t²+ 5t

• (je) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Exemple 3 : La longueur d'un rectangle est cinq fois sa largeur, exprimez l'aire du rectangle en fonction de sa longueur.

Solution:

Soit la longueur du rectangle l et la largeur du rectangle égale b

Maintenant,

• b = l/5

Aire du rectangle (A) = l × l/5 = l²/5

Ainsi, l’aire du rectangle en fonction de sa longueur est :

UNE(l) = l ² /5

Problèmes pratiques sur ce qu'est une fonction

1. Étant donné la fonction f(x)=3x+5

• Trouver f(2)
• Trouver f(−1)
• Déterminez le domaine et la plage de la fonction.

2. Étant donné la fonction g(x)=x ² – 4x + 3

• Trouvez les racines de la fonction.
• Trouvez g(3) et g(0).
• Déterminez le sommet de la fonction.

3. Étant donné deux fonctions f(x)=x + 2 et h(x)=2x – 3

• Trouver la fonction composée (f ∘ h) (x)
• Évaluer (f ∘ h)(2)

Résumé - Qu'est-ce qu'une fonction

Une fonction en mathématiques est une relation spéciale entre les valeurs d'entrée (domaine) et les valeurs de sortie (plage) où chaque entrée est associée à une sortie unique. Représentées par y = f(x), les fonctions ont des caractéristiques spécifiques et peuvent être visualisées à l'aide de paires ordonnées, de tableaux ou de graphiques. Ils sont essentiels dans divers problèmes mathématiques et se présentent sous différents types, notamment injectifs (un à un), surjectifs (sur) et bijectifs (les deux). Les fonctions peuvent être testées à l'aide du test de la ligne verticale et sont classées en fonctions polynomiales, inverses, exponentielles, logarithmiques et trigonométriques. Comprendre les fonctions implique de reconnaître leur domaine, leur étendue et les règles qui les définissent. Les exemples incluent des fonctions linéaires simples comme y = 2x + 1 et des compositions complexes de fonctions. Les fonctions jouent un rôle crucial en algèbre, en géométrie et en calcul, aidant à la représentation et à l'analyse des relations mathématiques et des phénomènes du monde réel.

FAQ sur ce qu'est une fonction

Quelle est la définition d’une fonction ?

Une relation f définie sur un ensemble A avec un autre ensemble B est appelée une fonction en mathématiques si chaque valeur de A a une valeur unique dans l'ensemble B.

Comment écrire une fonction en mathématiques ?

La fonction f en mathématiques est représentée par f : A → B et est définie comme, f(x) = x + 2. Ici, pour chaque valeur unique de x, nous avons une valeur unique de y.

Comment transformer une fonction ?

Nous pouvons facilement transformer une fonction en d’autres fonctions en effectuant simplement des opérations algébriques de base sur la fonction. Les différentes transformations de la fonction sont la réflexion, la translation, la rotation, etc.

Qu'est-ce qu'une fonction rationnelle ?

Une fonction fraction où le numérateur et le dénominateur sont des fonctions polynomiales est appelée fonction rationnelle. Quelques exemples de fonction rationnelle sont,

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), etc.

Qu'est-ce qu'une fonction linéaire ?

Une fonction algébrique dans laquelle chaque terme de la fonction est constant ou a une puissance de un est appelée fonction linéaire. Quelques exemples de fonction linéaire sont,

• f(x) = 2x + 3
• g(x) = x – 5, etc.

Que sont le domaine et le codomaine d’une fonction ?

Si nous définissons la fonction comme, y = f(x). Ensuite, le domaine de x est constitué de toutes les valeurs de x pour lesquelles y donne une valeur unique. Et le co-domaine de y est l'ensemble de toutes les valeurs de y pour chaque valeur de x.

Comment identifier une fonction en mathématiques ?

Si une valeur d'entrée (x) du domaine dans une relation a plus d'une image (y), alors cette relation ne peut jamais être une fonction. Donc si la valeur de x est répétée dans la paire ordonnée alors ce n’est jamais une fonction.