Les nombres complexes sont la continuation naturelle des nombres réels. À l’ère moderne, les nombres complexes sont utilisés dans de nombreux domaines tels que le traitement du signal numérique, la cryptographie et de nombreux domaines liés à l’informatique.

Dans cet article, nous découvrirons les nombres imaginaires, les nombres complexes et leur type, diverses opérations sur les nombres complexes, les propriétés des nombres complexes, l'application des nombres complexes, etc.

Définition des nombres complexes

Nombres complexes sont les Nombres de la forme (a + je b) où un & b sont les vrais chiffres et je est une unité imaginaire appelée iota qui représente √-1. Par exemple, 2 + 3i est un nombre complexe dans lequel 2 est un nombre réel et 3i est un nombre imaginaire. Les nombres complexes peuvent s'écrire sous la forme a + ib où a et b sont des nombres rationnels qui peuvent être représentés sur une droite numérique s'étendant jusqu'à infini .

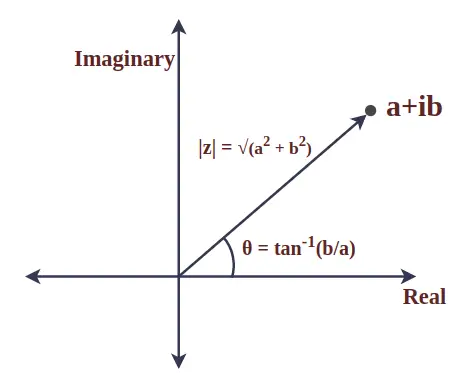
Module du nombre complexe

Le module du nombre complexe est la valeur absolue et représente la distance entre l'origine et le point donné. Elle est également connue sous le nom de grandeur du nombre complexe. Considérons un nombre complexe z = a + ib alors le module de z est défini comme :

|z| = √(une ² + b ² )

où,

• un est la partie réelle du nombre complexe z, et
• b est la partie imaginaire du nombre complexe z.

Argument du nombre complexe

L'angle entre le rayon vecteur d'un nombre complexe et l'axe des x positif est appelé argument d'un nombre complexe. Pour un nombre complexe z = a + ib, il est mathématiquement donné par :

θ = bronzage ^-1 (b/a)

où,

• un est la partie réelle du nombre complexe z, et
• b est la partie imaginaire du nombre complexe z.

Puissance de i(iota)

Le i(iota) est défini comme la racine carrée de -1. Ainsi, toute puissance de i peut être exprimée comme une multiplication répétée de i par elle-même, c'est-à-dire

• je = √(-1)
• je²= -1
• je³= – je
• je⁴= 1
• je⁵= je
• je⁶= – 1
• et ainsi de suite..

Besoin de nombres complexes

Dans les temps anciens, les gens ne connaissaient que les nombres naturels. Nombres sont de nature plus intuitive, car le cerveau humain les comprend déjà à l’aide d’images d’objets tels que les moutons et la nourriture. Ainsi, nous n’avons que l’ensemble des nombres naturels ( N ) mais en nombres naturels, il n'y a pas de solution à l'équation x + a = b (a> b) et a, b ∈ N. Ainsi, une extension des nombres naturels a vu le jour, c'est-à-dire Integers( je ).

Maintenant, encore une fois dans cet ensemble de nombres, il n’y a pas de solution à l’équation ax = b (a ≠ 0) et a, b ∈ I, où a et b sont tous deux des nombres entiers. Ainsi, un ensemble d'entiers (I) est étendu à un ensemble de nombres rationnels ( Q ).

lexicographiquement

Encore une fois, dans cet ensemble de nombres rationnels, il n’y a pas de solution à l’équation x²= a (a> 0) et a ∈ Q. Ainsi, Q est étendu pour inclure des nombres tels que, x²= a (pour a> 0), c'est-à-dire des nombres irrationnels. Cet ensemble est nommé Nombres réels et est représenté par R. .

Or, on a longtemps pensé qu’il n’était pas nécessaire d’étendre cet ensemble de nombres réels pour former un autre ensemble plus grand, car cet ensemble de nombres semble complet. Mais encore une fois, un nouveau problème se pose dans cet ensemble de nombres : il n’existe pas de nombre réel tel que x²= a (a <0) et a ∈ R. Ainsi, l'ensemble des nombres réels est étendu davantage pour inclure tous ces nombres complexes valorisés et nommés cet ensemble et est représenté par C .

Classification des nombres complexes

Comme nous le savons, la forme standard d'un nombre complexe est z = (une + je b) où a, b ∈ R et i est iota (une unité imaginaire). Ainsi en fonction des valeurs de a (appelée partie réelle) et b (appelée partie imaginaire), les nombres complexes sont classés en quatre types :

• Numéro complexe zéro
• Des nombres purement réels
• Nombres purement imaginaires
• Nombres imaginaires

Apprenons ces types en détail.

Numéro complexe zéro

Pour tout nombre complexe z = a + ib si a = 0 & b = 0, alors le nombre complexe est appelé nombre complexe zéro. Par exemple, le seul exemple est 0.

Des nombres purement réels

Pour tout nombre complexe z = a + ib si a ≠ 0 & b = 0, alors le nombre complexe est appelé un nombre purement réel, c'est-à-dire un nombre sans partie imaginaire. Tous les nombres réels en sont des exemples tels que 2, 3, 5, 7, etc.

Nombres purement imaginaires

Pour tout nombre complexe z = a + ib si a = 0 & b ≠ 0, alors un nombre complexe est appelé un nombre purement imaginaire, c'est-à-dire un nombre sans partie réelle. Tous les nombres sans parties réelles sont des exemples de ce type de nombre, c'est-à-dire -7i, -5i, -i, i, 5i, 7i, etc.

Nombres imaginaires

Pour tout nombre complexe z = a + ib si a ≠ 0 & b ≠ 0, alors un nombre complexe est appelé un nombre imaginaire . Par exemple, (-1 – i), (1 + i), (1 – i), (2 + 3i), etc.

Différentes formes de nombres complexes

Il existe différentes formes de nombres complexes qui sont,

• Forme rectangulaire
• Forme polaire
• Forme exponentielle

Découvrons-les maintenant en détail.

Forme rectangulaire

Forme rectangulaire est aussi appelé Forme standard et il est représenté par (a + ib), où a et b sont les nombres réels.

Par exemple : (5 + 5i), (-7i), (-3 – 4i), etc.

Forme polaire

Forme polaire est la représentation d'un nombre complexe où les coordonnées polaires [où les coordonnées sont représentées par (r, θ), où r est la distance à l'origine et θ est l'angle entre la ligne joignant le point et l'origine et l'axe des x positif) sont utilisés pour représenter un nombre complexe. Tout nombre complexe est représenté par r [cos θ + je péché θ].

Par exemples : [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6], etc.

Forme exponentielle

Formes exponentielles de nombres complexes est la représentation des nombres complexes en utilisant la formule d'Euler et sous cette forme, le nombre complexe est représenté par re^je, où r est la distance d'un point à l'origine et θ est l'angle entre l'axe des x positif et le rayon vecteur.

Par exemples : e^je(0), C'est^je(π/2), 5.e^je(π/6), etc.

Note: Les trois formes des nombres complexes évoquées ci-dessus sont interconvertibles, c'est-à-dire qu'elles peuvent être converties très facilement d'une forme à une autre.

Opérations sur les nombres complexes

Les opérations suivantes peuvent être effectuées sur les nombres complexes :

• Ajout
• Soustraction
• Multiplication
• Division
• Conjugaison

Ajout de nombres complexes

Nous pouvons additionner deux nombres complexes, en ajoutant simplement leurs parties réelles et imaginaires séparément.

Par exemple, (3 + 2i) + (1 + 4i) = 4 + 6i.

Soustraction de nombres complexes

Nous pouvons soustraire deux nombres complexes, en soustrayant simplement leurs parties réelle et imaginaire séparément.

Par exemple, (3 + 2i) – (1 + 4i) = 2 – 2i.

Multiplication de nombres complexes

On peut multiplier deux nombres complexes en utilisant la propriété distributive et le fait que je²= -1.

Par exemple, (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Division des nombres complexes

Nous pouvons diviser un nombre complexe par un autre, en multipliant simplement le numérateur et le dénominateur par le conjugué complexe du dénominateur et en simplifiant davantage l'expression.

Par exemple, (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Conjugaison de nombres complexes

On retrouve facilement le conjugué d'un nombre complexe, en changeant simplement le signe de sa partie imaginaire. Le conjugué d'un nombre complexe est souvent désigné par une barre au-dessus du nombre, comme z̄.

Par exemple, le conjugué de 3 + 2i est 3 – 2i.

Identités pour les nombres complexes

Pour deux nombres complexes quelconques z₁et z₂les identités algébriques suivantes peuvent être données :

• (Avec ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ ×z ₂
• (Avec ₁ - Avec ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2z ₁ ×z ₂
• (Avec ₁ ) ² - (Avec ₂ ) ² = (z ₁ +z ₂ )(Avec ₁ - Avec ₂ )
• (Avec ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Avec ₂ +3(z ₂ ) ² Avec ₁ + (z ₂ ) ³
• (Avec ₁ - Avec ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² Avec ₂ +3(z ₂ ) ² Avec ₁ - (Avec ₂ ) ³

Formules liées aux nombres complexes

Il existe quelques formules liées aux nombres complexes, dont certaines sont les suivantes :

programmation stdin c

Formule d'Euler

La formule d'Euler montre la relation entre la puissance imaginaire de l'exposant et le rapport trigonométrique sin et cos et est donnée par :

C'est ^ix = cos x + je péché x

De Moivre’s Formula

De Moivre’s Formula exprime le n^èmepuissance d'un nombre complexe sous forme polaire et est donnée par :

(cos x + je péché x) ⁿ = cos(nx) + je péché(nx)

Plan complexe

Le plan sur lequel les nombres complexes sont représentés de manière unique est appelé plan complexe ou plan d'Argand ou plan gaussien.

Le plan Complexe a deux axes :

• Axe X ou axe réel
• Axe Y ou axe imaginaire

Axe X ou axe réel

• Tous les nombres complexes purement réels sont représentés de manière unique par un point.
• La partie réelle Re(z) de tous les nombres complexes est tracée par rapport à elle.
• C'est pourquoi l'axe X est également appelé Axe réel .

Axe Y ou axe imaginaire

• Tous les nombres complexes purement imaginaires sont représentés de manière unique par un point.
• La partie imaginaire Im(z) de tous les nombres complexes est tracée par rapport à elle.
• C'est pourquoi l'axe Y est également appelé Axe imaginaire .

Représentation géométrique des nombres complexes

Comme nous savons que chaque nombre complexe (z = a + i b) est représenté par un point unique p(a, b) sur le plan complexe et que chaque point du plan complexe représente un nombre complexe unique.

Pour représenter n'importe quel nombre complexe z = (a + i b) sur le plan complexe, suivez ces conventions :

• La partie réelle de z (Re(z) = a) devient l'abscisse du point p

• Partie imaginaire de z (Im(z) = b) devient la coordonnée Y du point p

Et enfin z (a + i b) ⇒ p (a, b) qui est un point sur le plan complexe.

Propriétés des nombres complexes

Il existe diverses propriétés des nombres complexes, dont certaines sont les suivantes :

• Pour tout nombre complexe z = a + ib, si z = 0 alors a = 0 ainsi que b = 0.
• Pour 4 nombres réels a, b, c et d tels que z₁= a + ib et z₂= c + identifiant. Si z₁= z₂alors a = c et b = d.
• L'ajout d'un nombre complexe avec son conjugué donne un nombre purement réel, c'est-à-dire z + z̄ = nombre réel.

Soit z = a + ib,

z + z̄ = a + un + a – un

⇒ z + z̄ = 2a (ce qui est purement réel)

• Le produit d'un nombre complexe avec ses résultats conjugués est également un nombre purement réel, c'est-à-dire z × z̄ = Nombre réel

Soit z = a + ib, alors

z × z̄ = (a + un) × (a – un)

⇒ z × z̄= une²- je²b²

⇒ z × z̄ = une²+ b²(ce qui est purement réel)

• Les nombres complexes sont commutatif sous l’opération d’addition et de multiplication. Considérons deux nombres complexes z₁et z₂, et puis

Avec ₁ +z ₂ = z ₂ +z ₁

Avec ₁ ×z ₂ = z ₂ ×z ₁

• Les nombres complexes sont associatif avec l'opération d'addition et de multiplication. Considérons trois nombres complexes z₁, Avec₂, et z₃alors

(Avec ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Avec ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Les nombres complexes détiennent le propriété distributive de multiplication sur addition également. Considérons trois nombres complexes z₁, Avec₂, et z₃alors

Avec ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

En savoir plus,

• Division de nombres complexes
• Barre Z dans les nombres complexes

Exemples sur les nombres complexes

Exemple 1 : Tracez ces nombres complexes z = 3 + 2i sur le plan Complexe.

Solution:

Donné:

Avec = 3 + 2 je

Le point est donc z(3, 2). Maintenant, nous traçons ce point sur le graphique ci-dessous, ici dans ce graphique, l'axe des x représente la partie réelle et l'axe des y représente la partie imaginaire.

Exemple 2 : tracez ces nombres complexes z ₁ = (2 + 2 je), z ₂ = (-2 + 3 je), z ₃ = (-1 – 3 je), z ₄ = (1 – i) sur le plan complexe.

Solution:

Donné:

Avec₁= (2 + 2 je)

Avec₂= (-2 + 3 je)

Avec₃= (-1 – 3 je)

Avec₄= (1 – je)

Donc les points sont z₁(2, 2),z₂(-2, 3),z₃(-1, -3) et z₄(1, -1). Maintenant, nous traçons ces points sur le graphique ci-dessous, ici dans ce graphique, l'axe des x représente la partie réelle et l'axe des y représente la partie imaginaire.

FAQ sur les nombres complexes

Définir des nombres complexes.

Les nombres de la forme a+ib sont appelés nombres complexes, où a et b sont le nombre réel et i est l'unité imaginaire qui représente la racine carrée de -1.

Quelle est la différence entre un nombre réel et un nombre complexe ?

La différence entre les nombres réels et complexes est que nous n’avons besoin que d’un seul nombre pour représenter un nombre réel, mais que nous avons besoin de deux nombres réels pour représenter un nombre complexe.

Quelle est la partie réelle et la partie imaginaire d’un nombre complexe ?

Dans un nombre complexe a + ib, a est la partie réelle du nombre complexe et b est appelé la partie imaginaire du nombre complexe.

Quel est le conjugué complexe d’un nombre complexe ?

Pour un nombre complexe a + ib, a – ib est appelé son conjugué complexe. Des conjugués complexes peuvent être trouvés en changeant simplement le signe de la partie imaginaire.

Quel est le module d'un nombre complexe ?

La distance entre l'origine et le point représenté par un nombre complexe dans le plan argand est appelée module de ce nombre complet et pour z = a + ib, elle est mathématiquement donnée par :

|z| = √(une ² + b ² )

méthodes de chaîne en Java

Quel est l’argument d’un nombre complexe ?

L'angle entre le rayon vecteur d'un nombre complexe et l'axe des x positif est appelé argument d'un nombre complexe et pour z = a + ib, il est mathématiquement donné par :

θ = bronzage ^-1 (b/a)

Quelle est la forme polaire d'un nombre complexe ?

Pour tout nombre complexe, z = a + ib, sa forme polaire est donnée par :

r [cos θ + je péché θ]

Quelle est la formule d’Euler ?

La formule d'Euler montre la relation entre la puissance imaginaire de l'exposant et le rapport trigonométrique sin et cos et est donnée par :

C'est ^ix = cos x + je péché x