le Fonction cosinus ou la parce que la fonction en bref est une des six Fonctions trigonométriques fondamental en trigonométrie. Le cosinus en trigonométrie est donné comme le rapport de la base à l'hypoténuse d'un triangle rectangle. La fonction cosinus est représentée par Cos x où x est l'angle pour lequel le rapport cosinus est calculé. En termes de fonction, on peut dire que x est l'entrée ou le domaine de la fonction cosinus.

Il est largement utilisé dans un large éventail de sujets tels que la physique, la géométrie et l'ingénierie, entre autres, généralement en tirant parti de sa nature périodique. Par exemple, il est utilisé pour définir la nature ondulatoire des ondes sonores, les calculs du flux électrique à travers une surface plane, etc. Dans cet article, nous apprenons en détail ce qu'est la fonction cosinus, la domaine et plage de la fonction cosinus, la période et le graphique de la fonction cosinus.

Table des matières

• Qu'est-ce que la fonction cosinus ?
• Cos dans le cercle unitaire
• Graphique de la fonction cosinus
• Inverse de la fonction cosinus
• Fonction cosinus dans le calcul
• Identités de fonction Cos

Qu'est-ce que la fonction cosinus ?

La fonction cosinus est une fonction trigonométrique de nature fondamentalement périodique. La fonction cosinus est exprimée par cos x où x est l'un des angles aigus d'un triangle rectangle. La fonction cosinus trouve le rapport entre la base et l'hypoténuse pour une valeur donnée de x. La fonction cosinus est abrégée en cos(x) ou cos(θ) où x est l'angle en radians et theta θ est l'angle en degrés en général. La fonction cosinus peut être définie à l'aide d'un cercle unité, c'est-à-dire un cercle de rayon unité comme nous le verrons plus loin dans cet article. Il est de nature périodique et répète ses valeurs après chaque rotation complète des angles. Sur un plan cartésien, on peut l'appeler la composante vectorielle de l'hypoténuse parallèle à l'axe des x.

Définition de la fonction cosinus

La fonction cosinus est définie dans un triangle rectangle comme le rapport de la longueur du côté adjacent à l'angle concerné à la longueur de l'hypoténuse. Mathématiquement, la fonction cosinus est donnée comme

Cos x = Cos θ = Longueur de la base/Longueur de l'hypoténuse = b/h = OB/OA

où X est l'angle en radians et θ est l'angle équivalent en degrés.

Domaine et plage de la fonction Cos

Nous savons que pour une fonction, le domaine correspond aux valeurs d'entrée autorisées et la plage est la valeur de sortie pour cette entrée ou cette valeur de domaine particulière. Par conséquent, nous pouvons supposer que la fonction agit comme un processeur qui prend les entrées, les traite et donne une sortie particulière. Le domaine et la plage de la fonction cos sont décrits ci-dessous :

• Domaine de la fonction cosinus : R. c'est-à-dire un ensemble de tous les nombres réels.
• Plage de la fonction cosinus : [-1, 1], c'est-à-dire que la sortie varie entre tous les nombres réels entre -1 et 1.

Période d'une fonction cosinus

Le fonction est de nature périodique, c'est-à-dire qu'il se répète après 2π ou 360°. En d’autres termes, il se répète après chaque rotation complète. Par conséquent, la période de la fonction cosinus est une rotation complète ou un angle de 360° (ou 2π).

Réciproque d'une fonction cosinus

L’inverse d’une fonction cosinus est appelé sécante fonction ou seconde pour faire court. Mathématiquement, l'inverse de la fonction cosinus est donnée par

cas de test Junit

sec(θ) = 1/cos(θ)

Selon les règles de Réciproques , si l'on multiplie le Cos x par Sec x le produit sera toujours 1.

Graphique de la fonction cosinus

Le graphique de la fonction cosinus ressemble au graphique de la fonction sinus avec une différence fondamentale que pour x = 0, le graphique de la fonction sin passe de l'origine tandis qu'à x = 0, le graphique de la fonction cosinus passe de (0, 1) à y-aixs. Voici le graphique de la valeur de la fonction cosinus, c'est-à-dire y = cos x

Les propriétés discutées ci-dessus peuvent être vues dans le graphique comme la nature périodique de la fonction.

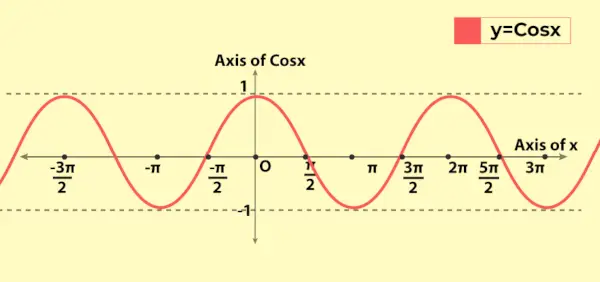
Variation de la fonction cosinus dans le graphique

Puisque la plage de la fonction cosinus est [-1, 1], elle varie donc de -1 à 1 dans le graphique. Il présente sa nature périodique lorsque le graphique se répète après chaque longueur 2π sur l'axe des x. Cela reflète que la fonction cosinus a une période de 2π (ou 360°).

Cos dans le cercle unitaire

La fonction cosinus peut être définie en utilisant le cercle unité. Voyons comment définir la fonction cosinus en termes de cercle unité.

Considérons un segment de droite OA tournant autour du point O où O est l'origine du plan cartésien. Ainsi, la rotation de OA décrit un cercle unité (cercle de rayon unité) centré à l'origine O et le point A se situe toujours sur ce cercle. Si nous déposons une perpendiculaire de A sur l'axe des x et appelons le point d'intersection B, et θ est l'angle que fait OA avec la direction positive de l'axe des x, alors cos(θ) = projection de l'hypoténuse sur x -axe = OB/|OA| = OB (puisque |OA| = 1 unité).

A noter que la direction OB est importante comme le montrent les figures suivantes. Le segment vert indique la longueur/magnitude et la flèche indique la direction (+ve ou -ve) de cos(θ)

Notez que la valeur de cos(θ) est positive pour θ appartenant aux premier et quatrième quadrants tandis qu'elle est négative pour θ appartenant aux deuxième et troisième quadrants.

Inverse de la fonction cosinus

L'inverse d'une fonction cosinus appelée arc-cosinus fonction et abrégé en arccos(x) ou parce que ^-1 (X) est défini comme suit

cos(x) = y

⇒ parce que ^-1 (y) = x

Domaine et plage de la fonction cosinus inverse

Le domaine et la plage de la fonction cosinus inverse sont mentionnés ci-dessous :

• Domaine de la fonction cosinus inverse : Tous les nombres réels compris dans la plage [-1, 1]
• Plage de fonction cosinus inverse : Tous les nombres réels dans la plage [0, π]

Fonction cosinus hyperbolique

Les fonctions hyperboliques sont l'équivalent analogique de la fonction trigonométrique dont l'expression algébrique est en termes de fonction exponentielle. La fonction cosinus hyperbolique abrégée en matraque(x) où X est un angle hyperbolique est un concept de géométrie hyperbolique. Comme (cos(x), sin(x)) représente un point sur un cercle unitaire, (cosh(x), sinh(x)) représente un point sur une hyperbole unitaire, c'est-à-dire xy = 1 où sinh(x) représente une hyperbolique fonction sinusoïdale. Le développement algébrique de la fonction cos hyperbolique est donné par

cosh(x) = (e ^X + et ^-X )/2

Plus de détails sur les fonctions hyperboliques dépassent le cadre de cet article, mais vous pouvez vous référer à Cet article .

Fonction cosinus dans le calcul

La branche du calcul en mathématiques traite des différenciation et intégration d'une fonction donnée. La différenciation de fonction est le taux de changement de la fonction par rapport à la variable indépendante tandis que l'intégration est le processus inverse de différenciation qui consiste à trouver l'intégrale d'une fonction dont la dérivée existe.

Dérivée de la fonction cosinus

Le dérivé de la fonction cosinus est égal au négatif de la fonction sinus. Mathématiquement

d(cos(x))/dx = -sin(x)

Intégration de la fonction cosinus

Le intégrale indéfinie de la fonction cosinus est égale à la fonction sinus. Mathématiquement –

∫cos(x)dx = sin(x) + C, où C est la constante d'intégration.

Fonctions sinus et cosinus

Le graphique suivant représente la principale différence entre les fonctions sinus et cosinus :

Différence entre les fonctions sinus et cosinus

Le tableau suivant répertorie les différences entre la fonction sinus et cosinus –

Tableau des valeurs du Cos

Le tableau suivant fournit les valeurs de la fonction cosinus pour certains angles courants dans le premier quadrant du plan cartésien –

Nous pouvons facilement calculer les valeurs d'autres angles courants comme 15°, 75°, 195°, -15°, etc. en utilisant ces valeurs en utilisant les formules cos (x + y) et cos (x – y) décrites plus loin dans ce document. article.

Vérifier, Tableau trigonométrique

Identités de fonction Cos

Les identités trigonométriques de base liées à la fonction cosinus sont mentionnées ci-dessous :

• sans²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/sec(x)
• cos 2x = cos²x – péché²x = 1 – 2péché²x = 2cos²x – 1 = (1 – bronzage²x/1 + bronzage²X)
• cos3x = 4cos³x – 3 cos x

Articles Liés

• Différenciation des fonctions trigonométriques
• Fonctions trigonométriques inverses
• Dérivés trigonométriques inverses

Exemples résolus sur la fonction cosinus

Voici quelques exemples résolus pour vous aider à mieux comprendre le concept de fonction cosinus.

Exemple 1 : Quelles sont les valeurs maximale et minimale de la fonction cosinus ?

Solution:

La valeur maximale de la fonction cosinus est de 1 à 0° et 180° tandis que la valeur minimale de la fonction est de -1 à 180°.

Exemple 2 : À quel(s) angle(s) dans la plage [0, 360] se trouve la valeur de la fonction cosinus 0 ?

Solution:

La valeur de la fonction cosinus est 0 aux angles 90° et 270°.

Exemple 3 : Pour quels quadrants la valeur de la fonction cosinus est-elle négative ?

Solution:

La fonction cosinus est négative dans le II^sdet III^rdquadrants.

Exemple 4 : Calculer la valeur de cos (45°).

Solution:

caractère Java en chaîne

Selon l'identité 4 donnée ci-dessus, cos(-x) = cos(x).

Donc cos(-45°) = cos(45°) = 1/√2

Exemple 5 : Calculer la valeur de cos(15°).

Solution:

Utilisation de l'identité 3 donnée ci-dessus -

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Exemple 6 : Qu'est-ce que cos ^-1 (1/2) dans la plage [0,π] ?

Solution:

Laissez parce que^-1(1/2) = oui.

Par conséquent, cos(y) = 1/2 ⇒ y = π/3 dans la plage donnée ci-dessus.

La réponse est donc π/3.

Exemple 7 : Quelle est la valeur de cos(-15°) ?

Solution:

En utilisant l’identité 3 donnée ci-dessus –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternativement, on peut également utiliser l'identité cos(-x) = cos(x) et utiliser la valeur de cos(15°) calculée dans l'exemple 5.

Exemple 8 : Calculez l'aire sous le graphique de la fonction cosinus pour x = 0 à x = π/2.

Solution:

L'aire donnée peut être calculée en résolvant l'intégrale définie suivante -

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

La réponse est donc 1 unité de carré.

Exemple 9 : Si cos(x) = π/3, trouvez la valeur de cos(3x) (sous forme décimale avec une précision de deux chiffres décimaux).

Solution:

Utiliser l'identité – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Exemple 10 : Trouvez la valeur de cos(120°).

Solution:

Utiliser l'identité pour cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 péché²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Questions pratiques : fonctions Cos

T1. Quelle est la formule pour calculer le cosinus d’un angle dans un triangle rectangle ?

Q2. Quelle est l’interprétation géométrique du cos sur le plan cartésien ?

Q3. Calculez la valeur de cos(120°).

Q4. Trouver la valeur de cos ^-1 (√3/2) dans la plage [π, 2π].

Q5. Si un poteau projette une ombre de même longueur sur le sol, trouvez l'angle du soleil par rapport au sol s'il est orienté vers l'est.

Résumé - Fonction cosinus

La fonction cosinus, notée cos(x), est une fonction trigonométrique fondamentale définie comme le rapport de la base à l'hypoténuse dans un triangle rectangle et est essentielle dans divers domaines comme la physique, l'ingénierie et la géométrie en raison de sa nature périodique. , qui joue un rôle déterminant dans la modélisation du comportement des vagues. Il a un domaine de tous les nombres réels et une plage de -1 à 1, répétant son cycle tous les 2 Pi radians ou 360 degrés, évident sur son graphique en forme de vague qui commence à (0,1). En termes de calcul, la dérivée de cos(x) est − sin( X ), et son intégrale donne sin( X )+ C , avec C comme constante d'intégration. Cette fonction s'étend également aux formes hyperboliques, telles que cosh(x), améliorant ainsi son application dans divers contextes et solutions mathématiques, notamment les calculs d'ondes et les oscillations dans les systèmes physiques.

Fonction cosinus : FAQ

1. Qu’est-ce que la fonction cosinus ?

La fonction cosinus est l'une des fonctions trigonométriques fondamentales. Elle est définie dans un triangle rectangle comme le rapport de la longueur du côté adjacent à l'angle concerné sur la longueur de l'hypoténuse.

2. Cos et cosinus sont-ils identiques en trigonométrie ?

Oui. cos est une abréviation/forme courte de la fonction cosinus.

3. Quelle est la plage de la fonction Cos ?

La plage du cos ou de la fonction cosinus est constituée de tous les nombres réels allant de -1 à 1, c'est-à-dire [-1,1].

4. Quel est le domaine de la fonction Cos ?

Le domaine du cos ou de la fonction cosinus est le ser de tous les nombres réels, c'est-à-dire R. .

5. Quelle est la valeur maximale de la fonction cosinus ?

La valeur maximale de la fonction cosinus est de 1 pour tous les angles équivalents à 0° ou 360°.

6. Quelle est la valeur minimale de la fonction cosinus ?

La valeur minimale de la fonction cosinus est de -1 pour tous les angles équivalents à 180°.

7. Comment trouver la valeur de Cos(-x) ?

La valeur de cos(-x) peut être calculée en calculant la valeur de cos(x) en raison de l'existence de l'identité suivante : cos(-x) = cos(x).

8. Comment représenter graphiquement la fonction cosinus ?

Pour dessiner le graphique de la fonction cosinus sur un plan cartésien, référez-vous à l'axe des x comme représentant les angles en radians (ou degrés) et à l'axe des y comme représentant les valeurs de la fonction cosinus pour l'angle correspondant sur l'axe des x. Maintenant,

• Étape 1: Prenez un sous-ensemble de l'axe des x pour lequel vous souhaitez dessiner le graphique.
• Étape 2: Divisez l'axe des x dans cette plage en points équidistants (c'est-à-dire qu'il y a un espace égal entre tous les sous-points). Notez que plus le nombre de divisions est grand, plus la précision du graphique résultant est grande.
• Étape 3: Pour chacun de ces sous-points x, marquez le point (x, cos(x)) sur le graphique.
• Étape 4: Joignez tous les points marqués pour obtenir le graphique de la fonction cosinus (pour le sous-ensemble de l'axe des x que vous avez sélectionné).

9. Comment trouver la période d'une fonction cosinus ?

La période d'une fonction cosinus fait référence à la plage minimale de valeurs après laquelle la fonction commence à se répéter. Nous savons que la fonction cosinus se répète après chaque rotation complète, ce qui signifie 2π radians. Par conséquent, la période de la fonction cosinus est de 2π radians ou 360°.

10. Qu'est-ce que l'amplitude d'une fonction cosinus ?

L'amplitude d'une fonction cosinus fait référence au déplacement maximal de la valeur de la fonction par rapport à la position moyenne, c'est-à-dire l'axe des x. L'amplitude de la fonction cosinus est de 1 puisque le déplacement maximum est de 1 (pour les valeurs -1 et 1 à 180 et 0 degrés respectivement. Notez que la plage de la fonction cosinus est [-amplitude, amplitude].