L'angle est mesuré en degrés (°) et en radians. Il est formé entre les deux côtés adjacents d'un polygone. Chaque polygone a des côtés différents et un nombre d'angles différent. La formule pour trouver les angles en degrés est utile en géométrie et en trigonométrie. Il est essentiel de comprendre d’autres concepts mathématiques, comme l’arc, l’angle au centre du cercle, etc.

1. Un cercle complet = 360°
2. Une ligne droite = 180°
3. Un demi-cercle = 180°
4. Un quart de cercle = 90°

Calculer des angles en degrés

Il existe trois méthodes différentes pour trouver des angles en degrés, qui sont les suivantes :

1. Utilisation du protecteur D
2. Utiliser le théorème de Pythagore et la fonction trigonométrique dans un triangle rectangle
3. Utiliser la formule de la somme des angles
4. Angle central d'un cercle

Utilisation du protecteur D

Un protecteur est un type de règle ou d’échelle utilisée pour mesurer la distance en centimètres ou en millimètres. Le protecteur utilisé pour mesurer les angles est en forme de « D » avec la valeur des angles marquée de 0 à 180° dans les deux sens (droite ou gauche). Nous devons aligner l’axe avec la ligne sur le D pour mesurer l’angle. Le cercle médian du protecteur est aligné sur le sommet de l’angle mesuré. Les rayons le long du sommet de l’angle aideront à trouver l’angle en degrés.

Utiliser le théorème de Pythagore et la fonction trigonométrique dans un triangle rectangle

En trigonométrie, il y a six fonctions, sinus, cos, cosec, bronzage, lit bébé, et seconde. Un triangle rectangle a trois côtés : une base, un perpendiculaire et une hypoténuse.

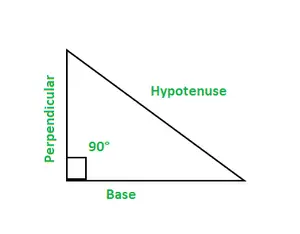
Base : C'est un côté adjacent à l'angle de 90°. Perpendiculaire : C'est aussi un côté adjacent à l'angle de 90°. Hypoténuse : C'est un côté opposé à l'angle de 90°.

Un triangle rectangle est représenté par un angle de 90° comme l'un des angles. La somme totale des angles d'un triangle est de 180°.

Cosecθ : Il est représenté par l'hypoténuse divisée par la perpendiculaire.

Cosecθ =

Cotθ : Il est représenté comme une base divisée par une perpendiculaire.

Lit bébéθ =

Les autres fonctions trigonométriques sont représentées comme suit :

péchéθ =

Cosθ =

tanθ =

secθ =

Cosecθ peut également être représenté par 1/ sinθ

secθ peut également être représenté par 1/ cosθ

Cotθ peut également être représenté par 1/ tanθ

Où,

Θ est l'angle

Théorème de Pythagore

Si deux côtés d’un angle droit sont connus, nous pouvons facilement calculer le troisième côté d’un triangle rectangle. Dans un triangle rectangle, le théorème de Pythagore est donné par :

(Hypoténuse)²= (Base)²+ (perpendiculaire)²

Formule de somme des angles

La somme des angles fait référence à la somme totale des angles internes d'un polygone se formant entre les deux côtés. S’il y a six côtés d’un polygone, il y a environ six angles. Il est utile de trouver un angle si d'autres angles et la somme des angles d'un polygone sont connus.

La formule pour trouver la somme totale des angles d’un polygone est donnée par :

Somme totale des angles = 180 (n – 2)

Où,

n est le nombre de côtés d'un polygone

Exemple:

• Si n = 4,

Somme totale des angles = 180 (4 – 2)

chaîne en java

= 180 (2)

= 360°

Si n = 5,

Somme totale des angles = 180 (5 – 2)

= 180 (3)

= 540°

• Si n = 6

Somme totale des angles = 180 (6 – 2)

= 180 (4)

= 720°

Angle central d'un cercle

Un cercle est une figure de forme ronde dont la limite est équidistante de son point central. La distance entre le point central et la limite est appelée rayon du cercle. L’angle formé par les deux rayons du cercle est appelé angle au centre. La valeur de l'angle au centre d'un cercle est comprise entre 0 et 360 degrés.

La formule pour calculer l’angle au centre d’un cercle est donnée par :

Longueur de l'arc = 2πr × (θ/360)

Θ = 360L/2pr

Où,

r est le rayon du cercle

AB est l'arc

Thêta est l'angle en degrés.

L = longueur de l'arc

Exemples de problèmes

Question 1 : Trouver l'angle au centre d'un cercle de rayon 2m avec une longueur d'arc de 4m ?

Solution :

La formule pour calculer l’angle au centre d’un cercle est donnée par :

Θ = 360L/2pr

Où,

r est le rayon du cercle

Thêta est l'angle en degrés.

L = longueur de l'arc

Θ = Angle en degrés

r = 2m

L = 4m

Θ = 360 × 4 /2 × π × 2

Θ = 114,6°

scanner.suivant java

Ainsi l'angle au centre du cercle est de 114,6°.

Question 2 : Trouver l'angle au centre d'un cercle de rayon 10 cm avec une longueur d'arc de 18 cm ?

Solution :

La formule pour calculer l’angle au centre d’un cercle est donnée par :

Θ = 360L/2pr

Où,

r est le rayon du cercle

Thêta est l'angle en degrés.

L = longueur de l'arc

r = 10 cm

L = 18 cm

Θ = Angle en degrés

Θ = 360 × 18 /2 × π × 10

Θ = 103,13°

Ainsi l'angle au centre du cercle est de 103,13°.

Question 3 : Trouvez l'angle d'un parallélogramme si les trois autres angles sont 80°, 95° et 105° ?

Solution :

tableau de retour Java

Il y a quatre côtés dans un parallélogramme dont la somme totale des angles est de 360°.

Formule pour trouver la somme des angles = 180 (n – 2)

Où,

n est le nombre de côtés d'un polygone

Ici, n = 4,

La somme totale des angles = 180 (4 – 2)

= 180 (2)

= 360°

Somme totale = Angle 1 + Angle 2 + Angle 3 + Angle 4

360 = 80+ 95+ 105+ Angle 4

360 = 280 + Angle 4

Angle 4 = 360 – 280

Angle 4 = 80°

Question 4 : Trouvez l'angle A dans la figure donnée.

Solution :

Donné : Hypoténuse = 12

Perpendiculaire = 6

La fonction trigonométrique pour calculer l’angle est donnée par :

péchéA = 6/12

A = 30°

Question 5 : Trouvez l’angle A dans la figure donnée.

Solution :

Donné : Hypoténuse = 10

Base= 5

La fonction trigonométrique pour calculer l’angle est donnée par :

CosA = 5/10

A = 60°

Question 6 : Trouvez l'angle d'un pentagone si les quatre autres angles sont 115°, 100°, 105° et 100° ?

Solution :

Il y a cinq côtés dans un pentagone dont la somme totale des angles est de 540°.

Formule pour trouver la somme des angles = 180 (n – 2)

combien de zéro pour un million

Où,

n est le nombre de côtés d'un polygone

Ici, n = 5,

Somme totale des angles = 180 (5 – 2)

= 180 (3)

= 540°

Somme totale = Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5

540 = 115° + 100° + 105°+100° + Angle 5

540 = 420 + Angle 5

Angle 5 = 540 – 420

Angle 5 = 120°

Question 7 : Trouvez l'angle A dans la figure donnée.

Solution :

Étant donné : Base = √3

Perpendiculaire= 1

La fonction trigonométrique pour calculer l’angle est donnée par :

tanθ =

tanθ = 1/√3

A = 30°

Question 8 : Trouvez l'angle d'un parallélogramme si les trois autres angles sont 100°, 70° et 80° ?

Solution :

Il y a quatre côtés dans un parallélogramme dont la somme totale des angles est de 360°.

Formule pour trouver la somme des angles = 180 (n – 2)

Où,

n est le nombre de côtés d'un polygone

Ici, n = 4,

Somme totale des angles = 180 (4 – 2)

= 180 (2)

= 360°

Somme totale = Angle 1 + Angle 2 + Angle 3 + Angle 4

360 = 100 + 70 + 80 + Angle 4

360 = 250 + Angle 4

valeur de la chaîne

Angle 4 = 360 – 250

Angle 4 = 110°

Ainsi, l'autre angle est de 110°.

Question 9 : Trouvez l'angle d'un hexagone si les cinq autres angles sont 120°, 115°, 110°, 125° et 105° ?

Solution :

Il y a six côtés dans un hexagone dont la somme totale des angles est de 720°.

Formule pour trouver la somme des angles = 180 (6 – 2)

Où,

n est le nombre de côtés d'un polygone

Ici, n = 6,

Somme totale des angles = 180 (6 – 2)

= 180 (4)

= 720°

Somme totale = Angle 1 + Angle 2 + Angle 3 + Angle 4 + Angle 5 + Angle 6

720 = 120 + 115 + 110 + 125 + 105 + Angle 6

720 = 575 + Angle 6

Angle 6 = 720 – 575

Angle 6 = 145°

Ainsi, le sixième angle de l’hexagone est de 145°.