Tableau de trigonométrie est un tableau standard qui nous aide à trouver les valeurs des rapports trigonométriques pour des angles standards tels que 0°, 30°, 45°, 60° et 90°. Il se compose des six rapports trigonométriques : sinus, cosinus, tangente, cosécante, sécante et cotangente.
Découvrons en détail la table trigonométrique.
Table des matières
- Tableau de trigonométrie
- Tableau des fonctions trigonométriques
- Astuce pour apprendre les rapports trigonométriques
- Comment mémoriser un tableau trigonométrique
- Comment créer une table de déclenchement
- Formules trigonométriques
- Tableau des identités trigonométriques
- Exemples de tableaux trigonométriques
Tableau de trigonométrie
Le tableau trigonométrique est la disposition des valeurs des six fonctions trigonométriques pour leurs angles communs sous forme de tableau.
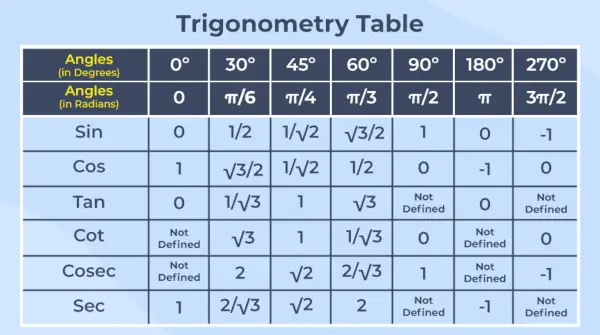
Note – La trigonométrie est une branche des mathématiques qui traite des relations entre les angles et les côtés des triangles rectangles.
Tableau des fonctions trigonométriques
La trigonométrie a 6 fonctions trigonométriques de base : sinus, cosinus, tangente, cosécante, sécante et cotangente. Examinons maintenant les fonctions trigonométriques.
Pour tout triangle rectangle avec perpendiculaire (P), base (B) et hypoténuse (H), les six fonctions trigonométriques sont les suivantes,
| Tableau des fonctions trigonométriques | |||
| Fonction | Définition | Représentation | Relation avec les côtés d'un triangle rectangle |
| Son | Rapport perpendiculaire et hypoténuse | sans je | Côté opposé / Hypoténuse |
| Cosinus | Rapport base/hypoténuse | parce que je | Côté adjacent / Hypoténuse |
| Tangente | Rapport du sinus et du cosinus d'un angle | donc je | Côté opposé / Côté adjacent |
| Cosécante | Réciproque du péché θ | csc je ou cosec je | Hypoténuse / Côté opposé |
| Sécante | Réciproque du cos θ | seconde je | Hypoténuse / Côté adjacent |
| Cotangente | Réciproque de tan θ | lit bébé je | Côté adjacent / Côté opposé |
Note – La trigonométrie est une branche des mathématiques qui traite des relations entre les angles et les côtés des triangles, en particulier des triangles rectangles. Cela implique l’étude et l’application des fonctions sinus, cosinus, tangente et autres fonctions trigonométriques pour résoudre des problèmes dans divers domaines.
Vérifier : Trigonométrie : formules, tableau, identités et rapports
Astuce pour apprendre les rapports trigonométriques
Étudiez le tableau ci-dessous pour apprendre les rapports trigonométriques d'une manière facile à retenir.
| Certaines personnes ont les cheveux noirs et bouclés pour produire de la beauté |
| sin θ (Certains) = Perpendiculaire (personnes) / hypoténuse (avoir) |
| cos θ (bouclé) = Base (noir) / hypoténuse (cheveux) |
| tan θ (à) = Perpendiculaire (produire) / Base (beauté) |
Comment mémoriser un tableau trigonométrique
Le tableau de trigonométrie est assez facile à retenir si vous connaissez toutes les formules de trigonométrie. Il existe également une astuce appelée truc à une main mémoriser la table de trigonométrie.

Étape 1: Dans la figure ci-dessus, pour la table des sinus, comptez les doigts du côté gauche pour l'angle standard.
Étape 2: Divisez le nombre de doigts du côté gauche (calculer à la 1ère étape) par 4
Étape 3: Trouvez la racine carrée de la valeur calculée à l'étape 2.
Vérifier: Formules trigonométriques – Liste de toutes les identités et formules trigonométriques
Comment créer une table de déclenchement
Étudiez les étapes suivantes pour créer la table trigonométrique pour les angles standard.
Étape 1 : Créer le tableau
Créez un tableau et répertoriez tous les angles tels que 0°, 30°, 45°, 60° et 90°, dans la rangée supérieure. Entrez toutes les fonctions trigonométriques sin, cos, tan, cosec, sec et cot dans la première colonne.
Étape 2 : Évaluez la valeur de tous les angles de la fonction sin.
Pour trouver les valeurs de la fonction sin, divisez 0, 1, 2, 3 et 4 par 4 et prenez sous la racine de chaque valeur, respectivement comme :
Car, la valeur de péché 0° = √(0/4) = 0
De la même manière,
péché 30° = √(1/4) = 1/2
péché 45° = √(2/4) = 1/√2
péché 60° = √(3/4) = √3/2
péché 90° = √(4/4) = 1
| sans 0° | sans 30° | sans 45° | sans 60° | sans 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
Étape 3: Évaluer la valeur pour tous les angles de la fonction cos
La valeur de la fonction cos est l'opposée de la valeur de la fonction sin c'est à dire cos 0° = sin 90°, cos 30° = sin 60° et cos 45° = sin 45°, donc
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Étape 4 : Évaluez la valeur pour tous les angles de la fonction tan
La valeur de la fonction tan est égale à la fonction sin divisée par la fonction cos, c'est-à-dire tan x = sin x / cos x. La valeur de tous les angles en fonction tan est calculée comme suit :
tan 0°= sin 0° / cos 0° = 0/1 = 0, de même
| donc 0° | donc 30° | donc 45° | donc 60° | donc 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Non défini |
Étape 5 : Évaluez la valeur pour tous les angles de la fonction cosec
La valeur de la fonction cosec est égale à l'inverse de la fonction sin. La valeur de cosec 0° est obtenue en prenant l'inverse de sin 0°
cosec 0° = 1 / sin 0° = 1 / 0 = Non défini. De la même manière,
couches de modèle osi
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Non défini | 2 | √2 | 23 | 1 |
Étape 6 : Évaluez la valeur pour tous les angles de la fonction sec
La valeur de la fonction sec est égale à l'inverse de la fonction cos. La valeur de sec 0° est obtenue en prenant l'inverse de cos 0°
sec 0° = 1 / cos 0° = 1 / 1 = 1. De même,
| seconde 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Non défini |
Étape 7 : Évaluez la valeur pour tous les angles de la fonction cot
La valeur de la fonction cot est égale à l'inverse de la fonction tan. La valeur de cot 0° est obtenue en prenant l'inverse de tan 0°
lit bébé 0° = 1 /tan 0° = 1 / 0 = Non défini. De la même manière,
| lit bébé 0° | lit bébé 30° | lit bébé 45° | lit bébé 60° | lit bébé 90° |
|---|---|---|---|---|
| Non défini | √3 | 1 | 1/√3 | 0 |
De cette façon, nous pouvons créer le tableau de rapports trigonométriques suivant :
| Tableau trigonométrique des degrés et des radians | |||||||
|---|---|---|---|---|---|---|---|
| Angle (en degrés) | Angle (en radians) | Sans | Parce que | Donc | Cosec | Seconde | Lit bébé |
| 0° | 0 | 0 | 1 | 0 | Indéfini | 1 | Indéfini |
| 30° | p/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Indéfini | 1 | Indéfini | 0 |
Formules trigonométriques
Découvrons quelques formules trigonométriques liées aux angles complémentaires et supplémentaires.
- Angles complémentaires: Paire d'angles dont la somme est égale à 90°
- Angles supplémentaires: Paire d'angles dont la somme est égale à 180°
Vérifier: Rapports trigonométriques
Identités trigonométriques d'angles complémentaires
Les identités des angles complémentaires sont basées sur la relation entre les fonctions trigonométriques de deux angles qui totalisent 90 degrés (ou π/2 radians). Ceux-ci sont connus sous le nom identités de co-fonction .
| Fonction trigonométrique | Identité |
|---|---|
| Son | péché(90°− je )=cos je |
| Cosinus | cos(90°− je )=sans je |
| Tangente | bronzage(90°− je )=lit bébé je |
| Cotangente | lit bébé(90°− je )=donc je |
| Sécante | sec(90°− je )=csc je |
| Cosécante | cosec(90°− je )=sec je |
Identités trigonométriques des angles supplémentaires
Les identités des angles supplémentaires concernent les fonctions trigonométriques de deux angles qui totalisent 180 degrés (ou π radians).
| Fonction trigonométrique | Identité |
|---|---|
| Son | péché(180°− je )=sans je |
| Cosinus | cos(180°− je )=−cos je |
| Tangente | bronzage(180°− je )=−bronze je |
| Cotangente | lit bébé(180°− je )=−lit bébé je |
| Sécante | sec(180°− je )=−sec je |
| Cosécante | cosec(180°− je )=cosec je |
Tableau des identités trigonométriques
Identités trigonométriques sont les identités très utilisées dans la résolution de problèmes trigonométriques. Il existe différentes identités trigonométriques mais les trois principales identités trigonométriques sont :
| Tableau des identités trigonométriques | |
| Identité trigonométrique | Formule |
| Identité pythagoricienne | sans2θ + cos2θ = 1 |
| Identité sécante-tangente | seconde2θ – donc2θ = 1 |
| Identité cosécante-cotangente | cosec2θ – lit bébé2θ = 1 |
Vérifiez également :
- Rapports trigonométriques
- Identités trigonométriques inverses
- Hauteurs et distances
Exemples de tableaux trigonométriques
Résolvons quelques questions sur la table trigonométrique.
Exemple 1 : Si sin θ = 4/5, alors trouvez toutes les valeurs trigonométriques.
Solution:
Ici nous avons,
péché θ = 4/5
télécharger YouTube avec VLCcomme, sin θ = Perpendiculaire / Hypoténuse
nous avons donc Perpendiculaire (P)= 4 et hypoténuse(H) = 5
Donc selon le théorème de Pythagore H 2 =P 2 +B 2
Découvrons la valeur de la base (B)
52=B2+ 42
25 = B2+ 16
25 -16 =B2
B2= 9
B = 3Maintenant nous avons,
Sin θ = Perpendiculaire/Hypoténuse
= AB/AC = 4/5Cosine θ = Base/Hypotenuse
= BC/AC = 3/5Tangente θ = Perpendiculaire/Base
= AB/BC = 4/3Cosécante θ = Hypoténuse/Perpendiculaire
= AC/AB = 5/4Secant θ = Hypotenuse/Base
= CA/BC = 5/3Cotangente θ = Base/Perpendiculaire
= BC/AB = 3/4
Exemple 2 : Trouvez la valeur de cos 45° + 2 sin 60° – tan 60°.
Solution:
De la table de trigonométrie,
cos 45° = 1/√2, sin 60° = √3/2 et tan 60° = √3
Ainsi,
cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Exemple 3 : Trouvez la valeur de cos 75°.
Solution:
Nous savons que,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Conclusion – Tableau de trigonométrie
La table de trigonométrie fournit une référence complète pour les fonctions trigonométriques sinus, cosinus, tangente, cosécante, sécante et cotangente, ainsi que leurs valeurs respectives pour différents angles. je t constitue un outil précieux pour résoudre équations trigonométriques, analyse des relations géométriques et compréhension du comportement des phénomènes périodiques. Que ce soit Mathématiques, physique, ingénierie ou autres domaines, la table trigonométrique facilite les calculs, la résolution de problèmes et la visualisation, contribuant à une compréhension plus approfondie des concepts trigonométriques et de leurs applications dans des scénarios du monde réel.
Table de trigonométrie – FAQ
Qu’est-ce que la trigonométrie ?
La trigonométrie est la branche des mathématiques qui traite des angles et des côtés de tout triangle.
Qu'est-ce qu'une table trigonométrique ?
Le tableau trigonométrique est un tableau qui contient les valeurs des six fonctions trigonométriques pour les angles communs.
Qui a inventé la table de trigonométrie ?
L'astronome grec Hipparque (127 avant JC) a inventé la table trigonométrique.
Que sont les angles standards dans un tableau trigonométrique ?
Les angles standard dans un tableau trigonométrique sont 0°, 30°, 45°, 60° et 90°
Quelle est la valeur du bronzage à 45 degrés ?
La valeur de tan 45 degrés est 1.
Comment apprendre la table de trigonométrie ?
L’astuce pour apprendre la table trigonométrique est la suivante :
- Vous devez apprendre toutes les valeurs de tous les angles de la fonction péché.
- La valeur de tous les angles de la fonction cos est l’image miroir de la fonction sin.
- Les valeurs de la fonction tan peuvent être calculées en divisant la fonction sin par la fonction cos.
- La valeur de la fonction cosec est réciproque du péché.
- De même, les fonctions sec et cot sont réciproques des fonctions cos et cot.
Quelles sont les six fonctions de base du tableau trigonométrique ?
Les six fonctions trigonométriques de base du tableau trigonométrique sont sinus, cosinus, tangente, sécante, cotangente et cosécante.
Existe-t-il des calculatrices qui peuvent remplacer les tables trigonométriques ?
Les calculatrices scientifiques peuvent calculer des rapports trigonométriques pour n’importe quel angle8.
A quoi sert une table de trigonométrie ?
Le tableau de trigonométrie est essentiellement utilisé pour trouver les valeurs de tous les rapports trigonométriques pour tous les angles. Ces valeurs ont un certain nombre d’applications réelles.
