Composants fortement connectés

Composants fortement connectés (SCC) sont un concept fondamental de la théorie des graphes et des algorithmes. Dans un graphe orienté, un Composant fortement connecté est un sous-ensemble de sommets où chaque sommet du sous-ensemble est accessible à partir de tous les autres sommets du même sous-ensemble en traversant les arêtes dirigées. Trouver le CSC d'un graphique peut fournir des informations importantes sur la structure et la connectivité du graphique, avec des applications dans divers domaines tels que analyse des réseaux sociaux, exploration du Web et routage réseau . Ce didacticiel explorera la définition, les propriétés et les algorithmes efficaces pour identifier les composants fortement connectés dans les structures de données graphiques.
Table des matières
- Qu'est-ce que les composants fortement connectés (SCC) ?
- Pourquoi les composants fortement connectés (SCC) sont-ils importants ?
- Différence entre les composants connectés et fortement connectés (SCC)
- Pourquoi la méthode DFS conventionnelle ne peut-elle pas être utilisée pour trouver des composants fortement connectés ?
- Connexion de deux composants fortement connectés par un bord unidirectionnel
- Approche par force brute pour trouver des composants fortement connectés
- Approche efficace pour trouver des composants fortement connectés (SCC)
- Conclusion
Qu'est-ce que les composants fortement connectés (SCC) ?
UN composant fortement connecté d'un graphe orienté est un sous-graphe maximal où chaque paire de sommets est mutuellement accessible. Cela signifie que pour deux nœuds A et B quelconques dans ce sous-graphe, il existe un chemin de A à B et un chemin de B à A.
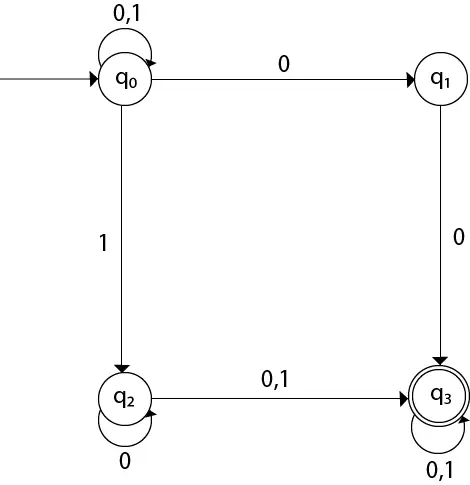
Par exemple: Le graphique ci-dessous comporte deux composants fortement connectés {1,2,3,4} et {5,6,7} puisqu'il existe un chemin de chaque sommet à chaque autre sommet dans le même composant fortement connecté.

Composant fortement connecté
Pourquoi les composants fortement connectés (SCC) sont-ils importants ?
Comprendre les SCC est crucial pour diverses applications telles que :
- Analyse de réseau : Identification de clusters de nœuds étroitement interconnectés.
- Optimisation des robots d'exploration Web : Détermination des parties du graphique Web qui sont étroitement liées.
- Résolution des dépendances : En logiciel, comprendre quels modules sont interdépendants.
Différence entre les composants connectés et fortement connectés ( CSC)
Connectivité dans un graphe non orienté fait référence à la question de savoir si deux sommets sont accessibles l'un à l'autre ou non. Deux sommets sont dits connectés s’il existe un chemin entre eux. Entre-temps Fortement connecté s'applique uniquement à graphiques orientés . Un sous-graphe d'un graphe orienté est considéré comme un Composants fortement connectés (CSC) si et seulement si pour chaque paire de sommets UN et B , il existe un chemin depuis UN à B et un chemin de B à UN . Voyons pourquoi le méthode dfs standard pour trouver les composants connectés dans un graphique ne peut pas être utilisé pour déterminer des composants fortement connectés.
Considérons le graphique suivant :

Maintenant, commençons un dfs appelez depuis le sommet 1 pour visiter d’autres sommets.

Pourquoi la méthode DFS conventionnelle ne peut-elle pas être utilisée pour trouver les composants fortement connectés ?
Tous les sommets peuvent être atteints à partir du sommet 1. Mais les sommets 1 et 5,6,7 ne peuvent pas être dans la même composante fortement connexe car il n'y a pas de chemin dirigé du sommet 5,6 ou 7 au sommet 1. Le graphe a deux sommets fortement connectés. composants connectés {1,2,3,4} et {5,6,7}. La méthode dfs conventionnelle ne peut donc pas être utilisée pour trouver les composants fortement connectés.
Connexion de deux composants fortement connectés par un bord unidirectionnel
Deux composants connectés différents deviennent un seul composant si une arête est ajoutée entre un sommet d'un composant et un sommet d'un autre composant. Mais ce n’est pas le cas dans les composants fortement connectés. Deux composants fortement connectés ne deviennent pas un seul composant fortement connecté s'il n'y a qu'un bord unidirectionnel d'un SCC à l'autre SCC.

Approche par force brute pour trouver des composants fortement connectés
La méthode simple sera pour chaque sommet i (qui ne fait partie d'aucune composante fortement) de trouver les sommets qui feront partie d'une composante fortement connexe contenant le sommet i. Deux sommets i et j seront dans la même composante fortement connectée s'il existe un chemin dirigé du sommet i au sommet j et vice-versa.
Comprenons l'approche à l'aide de l'exemple suivant :
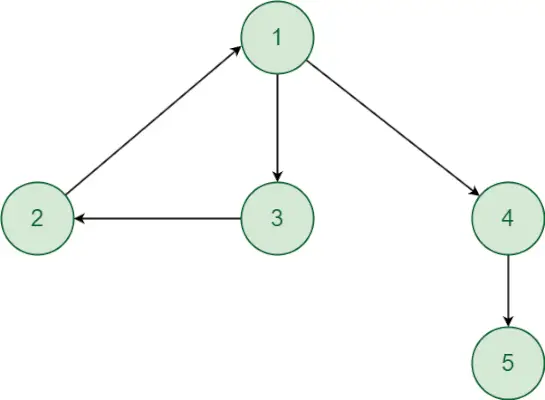
- En commençant par le sommet 1. Il existe un chemin du sommet 1 au sommet 2 et vice-versa. De même, il existe un chemin du sommet 1 au sommet 3 et vice versa. Ainsi, les sommets 2 et 3 seront dans le même composant fortement connecté que le sommet 1. Bien qu'il y ait un chemin dirigé du sommet 1 au sommet 4 et au sommet 5. Mais il n'y a pas de chemin dirigé du sommet 4,5 au sommet 1 donc le sommet 4 et 5 ne sera pas dans le même composant fortement connecté que le sommet 1. Ainsi, les sommets 1, 2 et 3 forment un composant fortement connecté.
- Pour les sommets 2 et 3, le composant fortement connecté a déjà été déterminé.
- Pour le sommet 4, il existe un chemin du sommet 4 au sommet 5 mais il n'y a pas de chemin du sommet 5 au sommet 4. Les sommets 4 et 5 ne seront donc pas dans le même composant fortement connecté. Ainsi, Vertex 4 et Vertex 5 feront partie d'un seul composant fortement connecté.
- Il y aura donc 3 composants fortement connectés {1,2,3}, {4} et {5}.
Vous trouverez ci-dessous la mise en œuvre de l’approche ci-dessus :
C++ #include using namespace std; class GFG { public: // dfs Function to reach destination bool dfs(int curr, int des, vector >& adj, vecteur & vis) { // Si le nœud curr est la destination, return true if (curr == des) { return true; } vis[curr] = 1; for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true; } } } renvoie faux ; } // Pour savoir s'il existe un chemin depuis la source vers // la destination bool isPath(int src, int des, vector >& adj) { vecteur vis(adj.size() + 1, 0); return dfs(src, des, adj, vis); } // Fonction pour renvoyer tous les composants // fortement connectés d'un graphe. vecteur > findSCC(int n, vecteur >& a) { // Stocke tous les composants fortement connectés. vecteur > ans; // Stocke si un sommet fait partie d'un vecteur de composant fortement // connecté est_scc(n + 1, 0); vecteur > adj(n + 1); pour (int je = 0; je < a.size(); i++) { adj[a[i][0]].push_back(a[i][1]); } // Traversing all the vertices for (int i = 1; i <= n; i++) { if (!is_scc[i]) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // thr part of thidl ist. vector cc; scc.push_back(i); pour (int j = i + 1; j <= n; j++) { // If there is a path from vertex i to // vertex j and vice versa put vertex j // into the current SCC list. if (!is_scc[j] && isPath(i, j, adj) && isPath(j, i, adj)) { is_scc[j] = 1; scc.push_back(j); } } // Insert the SCC containing vertex i into // the final list. ans.push_back(scc); } } return ans; } }; // Driver Code Starts int main() { GFG obj; int V = 5; vector > bords{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } } ; vecteur > ans = obj.findSCC(V, bords); cout < < 'Strongly Connected Components are:
'; for (auto x : ans) { for (auto y : x) { cout < < y < < ' '; } cout < < '
'; } } Java import java.util.ArrayList; import java.util.List; class GFG { // dfs Function to reach destination boolean dfs(int curr, int des, List > adj, Liste vis) { // Si le nœud curr est la destination, return true if (curr == des) { return true; } vis.set(curr, 1); for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true; } } } renvoie faux ; } // Pour savoir s'il existe un chemin depuis la source vers // la destination boolean isPath(int src, int des, List > adj) { Liste vis = new ArrayList(adj.size() + 1); pour (int je = 0; je <= adj.size(); i++) { vis.add(0); } return dfs(src, des, adj, vis); } // Function to return all the strongly connected // component of a graph. List > findSCC(int n, Liste > a) { // Stocke tous les composants fortement connectés. Liste > ans = new ArrayList(); // Stocke si un sommet fait partie d'une liste de composants // fortement connectés is_scc = new ArrayList(n + 1); pour (int je = 0; je <= n; i++) { is_scc.add(0); } List > adj = new ArrayList(); pour (int je = 0; je <= n; i++) { adj.add(new ArrayList()); } for (List bord : a) { adj.get(edge.get(0)).add(edge.get(1)); } // Parcours de tous les sommets pour (int i = 1; i <= n; i++) { if (is_scc.get(i) == 0) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // the part of this list. List scc = new ArrayList(); scc.add(i); pour (int j = i + 1; j <= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (is_scc.get(j) == 0 && isPath(i, j, adj) && isPath(j, i, adj)) { is_scc.set(j, 1); scc.add(j); } } // Insert the SCC containing vertex i into // the final list. ans.add(scc); } } return ans; } } public class Main { public static void main(String[] args) { GFG obj = new GFG(); int V = 5; List > bords = new ArrayList(); edge.add(new ArrayList(List.of(1, 3))); edge.add(new ArrayList(List.of(1, 4))); edge.add(new ArrayList(List.of(2, 1))); edge.add(new ArrayList(List.of(3, 2))); edge.add(new ArrayList(List.of(4, 5))); Liste > ans = obj.findSCC(V, bords); System.out.println('Les composants fortement connectés sont :'); pour (Liste x : ans) { for (int y : x) { System.out.print(y + ' '); } System.out.println(); } } } // Ce code est fourni par shivamgupta310570
Python class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570 C# using System; using System.Collections.Generic; class GFG { // dfs Function to reach destination public bool Dfs(int curr, int des, List > adj, Liste vis) { // Si le nœud curr est la destination, renvoie true if (curr == des) { return true; } vis[curr] = 1; foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true; } } } renvoie faux ; } // Pour savoir s'il existe un chemin de la source à la destination public bool IsPath(int src, int des, List > adj) { var show = nouvelle liste (adj.Count + 1); pour (int je = 0; je < adj.Count + 1; i++) { vis.Add(0); } return Dfs(src, des, adj, vis); } // Function to return all the strongly connected components of a graph public List > FindSCC(int n, Liste > a) { // Stocke tous les composants fortement connectés var ans = new List >(); // Stocke si un sommet fait partie d'un composant fortement connecté var isScc = new List (n+1); pour (int je = 0; je < n + 1; i++) { isScc.Add(0); } var adj = new List >(n+1); pour (int je = 0; je < n + 1; i++) { adj.Add(new List ()); } pour (int je = 0; je < a.Count; i++) { adj[a[i][0]].Add(a[i][1]); } // Traversing all the vertices for (int i = 1; i <= n; i++) { if (isScc[i] == 0) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // the part of this list. var scc = new List (); scc.Add(i); pour (int j = i + 1; j <= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj)) { isScc[j] = 1; scc.Add(j); } } // Insert the SCC containing vertex i into // the final list. ans.Add(scc); } } return ans; } } // Driver Code Starts class Program { static void Main(string[] args) { GFG obj = new GFG(); int V = 5; List > bords = nouvelle liste > { nouvelle liste { 1, 3 }, nouvelle liste { 1, 4 }, nouvelle liste { 2, 1 }, nouvelle liste { 3, 2 }, nouvelle liste { 4, 5 } } ; Liste > ans = obj.FindSCC(V, bords); Console.WriteLine('Les composants fortement connectés sont :'); foreach (var x dans ans) { foreach (var y dans x) { Console.Write(y + ' '); } Console.WriteLine(); } } } // Ce code est fourni par shivamgupta310570
Javascript class GFG { // Function to reach the destination using DFS dfs(curr, des, adj, vis) { // If the current node is the destination, return true if (curr === des) { return true; } vis[curr] = 1; for (let x of adj[curr]) { if (!vis[x]) { if (this.dfs(x, des, adj, vis)) { return true; } } } return false; } // Check whether there is a path from source to destination isPath(src, des, adj) { const vis = new Array(adj.length + 1).fill(0); return this.dfs(src, des, adj, vis); } // Function to find all strongly connected components of a graph findSCC(n, a) { // Stores all strongly connected components const ans = []; // Stores whether a vertex is part of any Strongly Connected Component const is_scc = new Array(n + 1).fill(0); const adj = new Array(n + 1).fill().map(() =>[]); pour (soit i = 0; i < a.length; i++) { adj[a[i][0]].push(a[i][1]); } // Traversing all the vertices for (let i = 1; i <= n; i++) { if (!is_scc[i]) { // If a vertex i is not part of any SCC, // insert it into a new SCC list and check // for other vertices that can be part of this list. const scc = [i]; for (let j = i + 1; j <= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) { is_scc[j] = 1; scc.push(j); } } // Insert the SCC containing vertex i into the final list. ans.push(scc); } } return ans; } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) { console.log(x.join(' ')); } // This code is contributed by shivamgupta310570 Sortir
Strongly Connected Components are: 1 2 3 4 5
Complexité temporelle : O(n * (n + m)), car pour chaque paire de sommets nous vérifions si un chemin existe entre eux.
Espace auxiliaire : O(N)
Approche efficace pour trouver des composants fortement connectés (SCC)
Pour trouver les SCC dans un graphique, nous pouvons utiliser des algorithmes comme L'algorithme de Kosaraju ou L'algorithme de Tarjan . Explorons ces algorithmes étape par étape.
1. L'algorithme de Kosaraju :
L'algorithme de Kosaraju comprend deux phases principales :
- Effectuer une recherche en profondeur (DFS) sur le graphique d'origine :
- Nous effectuons d'abord un DFS sur le graphique d'origine et enregistrons les heures de fin des nœuds (c'est-à-dire l'heure à laquelle le DFS termine l'exploration complète d'un nœud).
- Exécution de DFS sur le graphique transposé :
- Nous inversons ensuite la direction de toutes les arêtes du graphique pour créer le graphique transposé.
- Ensuite, nous effectuons une DFS sur le graphe transposé, en considérant les nœuds par ordre décroissant de leurs temps d'arrivée enregistrés dans la première phase.
- Chaque parcours DFS dans cette phase nous donnera un SCC.
Voici une version simplifiée de l’algorithme de Kosaraju :
- DFS sur le graphique original : Enregistrez les temps d’arrivée.
- Transposer le graphique : Inversez tous les bords.
- DFS sur graphique transposé : Traitez les nœuds par ordre décroissant des temps de fin pour trouver les SCC.
2. L'algorithme de Tarjan :
L'algorithme de Tarjan est plus efficace car il trouve les SCC en un seul passage DFS à l'aide d'une pile et d'une comptabilité supplémentaire :
- Traversée DFS : Pendant le DFS, conservez un index pour chaque nœud et le plus petit index (valeur de lien faible) pouvant être atteint depuis le nœud.
- Empiler : Gardez une trace des nœuds actuellement dans la pile de récursion (une partie du SCC actuel en cours d'exploration).
- Identifier les CSC : Lorsque la valeur du lien faible d'un nœud est égale à son index, cela signifie que nous avons trouvé un SCC. Extrayez tous les nœuds de la pile jusqu'à ce que nous atteignions le nœud actuel.
Voici un aperçu simplifié de l’algorithme de Tarjan :
- Initialiser
index>à 0. - Pour chaque nœud non visité, effectuez DFS.
- Définissez l'index du nœud et la valeur du lien faible.
- Poussez le nœud sur la pile.
- Pour chaque nœud adjacent, effectuez DFS s'il n'est pas visité ou mettez à jour la valeur du lien faible s'il est dans la pile.
- Si la valeur du lien faible du nœud est égale à son index, supprimez les nœuds de la pile pour former un SCC.
Conclusion
Comprendre et trouver composants fortement connectés dans un graphe orienté est essentiel pour de nombreuses applications en informatique. Kosaraju et de Tarjan Les algorithmes sont des moyens efficaces d’identifier les SCC, chacun avec sa propre approche et ses propres avantages. En maîtrisant ces concepts, vous pourrez mieux analyser et optimiser la structure et le comportement des réseaux complexes.