Exemple 1:
Concevez un NFA pour la table de transition comme indiqué ci-dessous :
| État actuel | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| →q3 | q3 | q3 |
Solution:
Le diagramme de transition peut être dessiné en utilisant la fonction de mappage comme indiqué dans le tableau.
méthode tostring en java
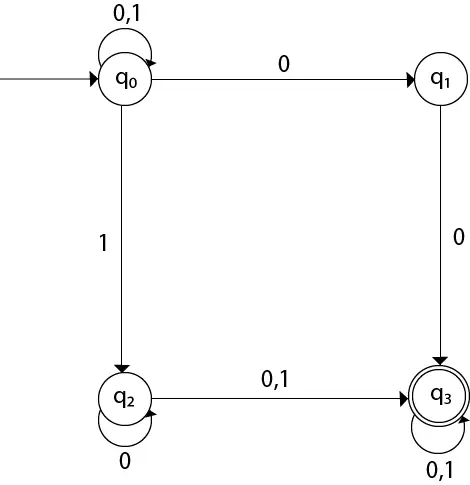
Ici,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Exemple 2 :
Concevoir un NFA avec ∑ = {0, 1} accepte toutes les chaînes se terminant par 01.
Solution:

Par conséquent, NFA serait :

Exemple 3 :
Concevez un NFA avec ∑ = {0, 1} dans lequel le double « 1 » est suivi du double « 0 ».
Solution:
Le FA avec double 1 est le suivant :

Il doit être immédiatement suivi du double 0.
Alors,

Maintenant, avant le double 1, il peut y avoir n'importe quelle chaîne de 0 et 1. De même, après le double 0, il peut y avoir n'importe quelle chaîne de 0 et 1.
La NFA devient donc :

Considérons maintenant la chaîne 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Exemple 4 :
Concevez un NFA dans lequel toute la chaîne contient une sous-chaîne 1110.
Solution:
Le langage est constitué de toute la chaîne contenant la sous-chaîne 1010. Le diagramme de transition partiel peut être :

Maintenant, 1010 pourrait être la sous-chaîne. Nous ajouterons donc les entrées 0 et 1 afin que la sous-chaîne 1010 du langage puisse être conservée. La NFA devient donc :

La table de transition pour le diagramme de transition ci-dessus peut être donnée ci-dessous :
| État actuel | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Considérons une chaîne 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Est resté coincé! Comme il n'y a pas de chemin depuis q2 pour le symbole d'entrée 0. Nous pouvons traiter la chaîne 111010 d'une autre manière.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Comme l'état q5 est l'état d'acceptation. Nous obtenons le scan complet et nous arrivons à l’état final.
Exemple 5 :
Concevoir un NFA avec ∑ = {0, 1} accepte toutes les chaînes dans lesquelles le troisième symbole à partir de l'extrémité droite est toujours 0.
Solution:

Ainsi, nous obtenons toujours le troisième symbole à partir de l’extrémité droite sous la forme « 0 ». Le NFA peut être :

L'image ci-dessus est une NFA car dans l'état q0 avec l'entrée 0, on peut soit passer à l'état q0, soit à q1.
