Analyse de la complexité temporelle et spatiale du tri par fusion
Le Complexité temporelle du tri par fusion est O (n journal n) dans les deux moyenne et pires cas . La complexité spatiale de Tri par fusion est Sur) .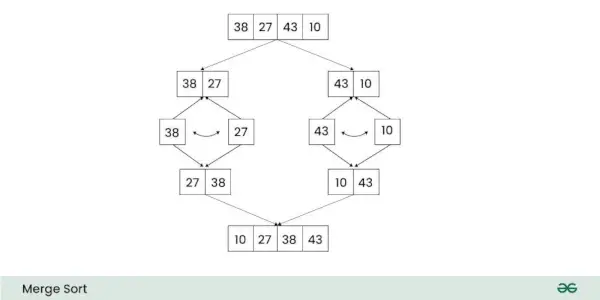 
| Aspect | Complexité |
|---|---|
| Complexité temporelle | O (n journal n) |
| Complexité spatiale | Sur) |
Analyse de complexité temporelle du tri par fusion :
Considérez les terminologies suivantes :
T(k) = temps nécessaire pour trier k éléments
M(k) = temps nécessaire pour fusionner k éléments
Donc on peut écrire
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + constante * N
Ces éléments N/2 sont ensuite divisés en deux moitiés. Donc,
T(N) = 2 * [2 * T(N/4) + constante * N/2] + constante * N
= 4 * T(N/4) + 2 * N * constante
. . .
= 2 k *T(N/2 k ) + k * N * constante
Il peut être divisé au maximum jusqu'à ce qu'il ne reste qu'un élément. Alors alors N/2 k = 1. k = journal 2 N
T(N) = N * T(1) + N * journal 2 N * constante
= N + N * journal 2 N
La complexité temporelle est donc O(N * journal 2 N) .
Ainsi, dans le meilleur des cas, le pire des cas et le cas moyen, la complexité temporelle est la même.
Analyse de la complexité spatiale du tri par fusion :
Tri par fusion a un complexité de l'espace de Sur) . C'est parce qu'il utilise un tableau auxiliaire de taille n pour fusionner les moitiés triées du tableau d’entrée. Le tableau auxiliaire est utilisé pour stocker le résultat fusionné et le tableau d'entrée est écrasé par le résultat trié.
