UN Graphe acyclique dirigé , souvent abrégé en JOUR , est un concept fondamental de la théorie des graphes. Les DAG sont utilisés pour montrer comment les choses sont liées ou dépendent les unes des autres de manière claire et organisée. Dans cet article, nous allons découvrir Graphe acyclique dirigé , ses propriétés et son application dans la vie réelle.

Graphe acyclique dirigé

Qu’est-ce que le graphique acyclique dirigé ?

UN Graphique acyclique dirigé (DAG) est un graphe orienté qui ne contient aucun cycle.

Le graphique ci-dessous représente un graphique acyclique dirigé (DAG) :

Graphique acyclique direct

Signification du graphique acyclique dirigé :

Le graphique acyclique dirigé présente deux fonctionnalités importantes :

• Bord dirigé s :Dans le graphique acyclique dirigé, chaque arête a une direction, ce qui signifie qu'elle va d'un sommet (nœud) à un autre. Cette direction signifie un Sens Unique relation ou dépendance entre les nœuds.
• Acyclique : Le terme acyclique indique qu'il n'y a pas de cycles ou de boucles fermées dans le graphique. En d’autres termes, vous ne pouvez pas parcourir une séquence d’arêtes dirigées et revenir au même nœud, en suivant les directions des arêtes. La formation de cycles est interdite dans JOUR. Cette caractéristique est donc essentielle.

Graphe acyclique dirigé

Propriétés du graphe acyclique dirigé DAG :

Les graphes acycliques dirigés (DAG) ont différentes propriétés qui les rendent utilisables dans les problèmes de graphes.

Il existe les propriétés suivantes du graphique acyclique dirigé (DAG) :

• Relation d'accessibilité : Dans DAG, nous pouvons déterminer s'il existe une relation d'accessibilité entre deux nœuds. Le nœud A est dit accessible depuis le nœud B s'il existe un chemin dirigé qui commence au nœud B et se termine au nœud A. Cela implique que vous pouvez suivre la direction des arêtes dans le graphique pour passer de B à A.
• Clôture transitive : La fermeture transitive d'un graphe orienté est un nouveau graphe qui représente toutes les relations ou connexions directes et indirectes entre les nœuds du graphe d'origine. En d’autres termes, il vous indique quels nœuds peuvent être atteints depuis d’autres nœuds en suivant un ou plusieurs arcs dirigés.

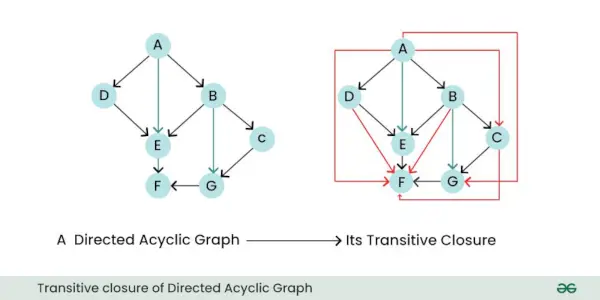
Fermeture transitive du graphe acyclique dirigé

• Réduction transitive : La réduction transitive d'un graphe orienté est un nouveau graphe qui conserve uniquement les relations directes essentielles entre les nœuds, tout en supprimant toutes les arêtes indirectes inutiles. Essentiellement, cela simplifie le graphique en éliminant les arêtes qui peuvent être déduites des arêtes restantes.

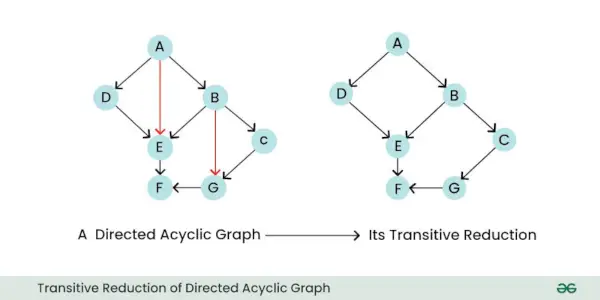
Réduction transitive du graphe acyclique dirigé

• Ordre topologique : Un DAG peut être trié topologiquement, ce qui signifie que vous pouvez ordonner linéairement ses nœuds de telle sorte que pour tous les tronçons, le nœud de départ du tronçon se produise plus tôt dans la séquence. Cette propriété est utile pour des tâches telles que la planification et la résolution des dépendances.

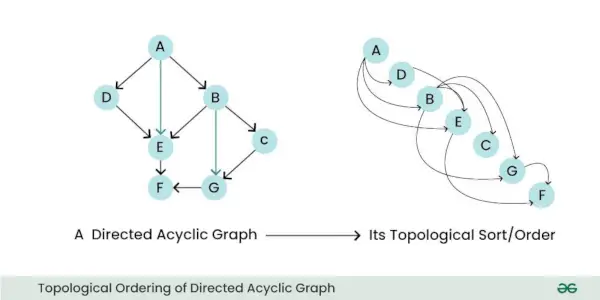
Ordre topologique du graphe acyclique dirigé

Applications pratiques du DAG :

• Analyse du flux de données : Dans la conception et l'optimisation du compilateur, les DAG sont utilisés pour représenter le flux de données au sein d'un programme. Cela aide à optimiser le code en identifiant les calculs redondants et le code mort. Les DAG sont également utilisés pour représenter la structure de blocs de base dans la conception du compilateur.

• Planification des tâches : Les DAG sont utilisés dans la gestion de projet et la planification des tâches. Chaque tâche ou travail est représenté comme un nœud dans le DAG, avec des bords dirigés indiquant les dépendances. La nature acyclique du DAG garantit que les tâches sont planifiées dans un ordre logique, évitant ainsi les dépendances circulaires.

Un graphe acyclique orienté pondéré peut être utilisé pour représenter un problème d’ordonnancement. Prenons l’exemple d’un problème de planification de tâches. Ici, un sommet peut représenter la tâche et son poids peut représenter la taille du calcul de la tâche. De même, un bord peut représenter la communication entre deux tâches et son poids peut représenter le coût de la communication :

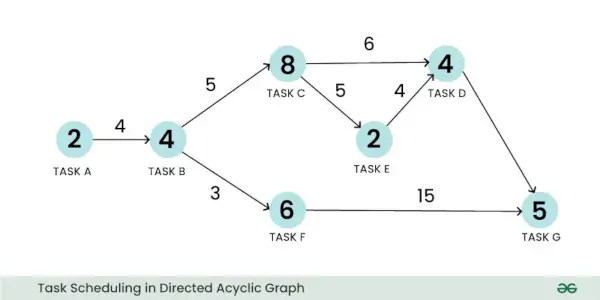
Planification des tâches dans un graphique acyclique dirigé

Conclusion:

En résumé, les graphes acycliques dirigés sont un concept fondamental de la théorie des graphes avec de nombreuses applications pratiques. Les DAG jouent un rôle crucial dans la planification des tâches, l’analyse des flux de données, la résolution des dépendances et divers autres domaines de l’informatique et de l’ingénierie. Ils aident à optimiser les processus, à gérer les dépendances et à garantir une exécution efficace des tâches ou des travaux.