Polygone en mathématiques est une forme bidimensionnelle composée de lignes droites qui forment une chaîne polygonale fermée. Le mot polygone vient des mots poly et gon, qui signifient plusieurs et côtés.
Les polygones peuvent être simples ou se croiser. Un simple polygone ne se coupe pas, sauf aux extrémités partagées de segments consécutifs. Une chaîne polygonale qui se croise crée un polygone qui se croise automatiquement. Les polygones peuvent également être classés comme concaves ou convexes.
Dans cet article, nous avons mentionné en détail les polygones et leurs types, formules et exemples.
| Faits importants sur les polygones | |
|---|---|
| Somme des angles intérieurs du polygone | (n–2) × 180° |
| Nombre de diagonales dans un polygone | n(n–3)/2 |
| Angle intérieur du polygone régulier | {(n–2) × 180°}/n |
| Angle extérieur du polygone régulier | 360°/n |
Table des matières
- Que sont les polygones ?
- Graphique polygonal basé sur le nombre de côtés
- Propriétés des polygones
- Formes de polygones
- Types de polygones
- Formules de polygones
- Angles dans les polygones
- FAQ
Que sont les polygones ?
Le terme « polygone » vient du mot grec polugonos, où « poly » signifie « plusieurs » et « gon » désigne « angle ». Généralement, un polygone est une figure fermée formée de lignes droites, avec ses angles intérieurs créés par celles-ci. lignes. Pour constituer une forme fermée, un minimum de trois segments de lignes est nécessaire. Il est communément appelé Triangle ou 3-gon. Le terme général désignant un polygone à n côtés est un n-gone.
Définition du polygone
Polygones sont des figures plates et bidimensionnelles composées de côtés droits qui forment une forme entièrement fermée. En géométrie, le polygone est une figure plane composée de segments de droite reliés pour former une chaîne polygonale fermée. Ils sont constitués de côtés droits et non de courbes, et peuvent avoir un nombre variable de côtés. Certains polygones de différents types sont : ouverts, délimités uniquement, fermés et auto-entrecroisés.
En géométrie, un polygone est défini comme une forme fermée et bidimensionnelle qui repose à plat dans un plan et est entourée de côtés droits.
Un polygone n'a pas de côtés incurvés et ses bords sont les segments droits définissant sa limite. Les points de rencontre de ces arêtes sont appelés sommets ou coins.
Exemples de polygones
En termes mathématiques, les triangles, les hexagones, les pentagones et les quadrilatères sont des exemples de polygones. Des exemples concrets de Polygon sont l'écran de forme rectangulaire de votre ordinateur portable, de votre téléviseur ou de votre téléphone portable ; terrain de football rectangulaire ou aire de jeux, Triangle des Bermudes et Pyramides égyptiennes de forme triangulaire.

Parties d'un polygone
Un polygone comprend trois composants fondamentaux :
- Côtés du polygone : Les côtés d'un polygone constituent la limite des polygones qui définissent la région fermée.
- Sommets : Le point où deux côtés se rencontrent est appelé sommet.
- Angles : Le polygone contient des angles intérieurs et extérieurs. Un angle intérieur est formé dans la région fermée du polygone par l'intersection de ses côtés.
Graphique polygonal basé sur le nombre de côtés
Nomenclature des polygones définie en fonction du nombre de côtés qu'ils possèdent. Il est désigné par n-gons, où « n » signifie le nombre de côtés. Les polygones sont généralement identifiés par la quantité de leurs arêtes. Par exemple, un polygone à cinq côtés est appelé 5-gones, tandis qu'un polygone à dix côtés est appelé 10-gones.
| Graphique polygonal | ||||
|---|---|---|---|---|
| Noms des formes de polygones | Nombre de côtés | Nombre de sommets | Nombre de diagonales | Mesure d'angle intérieur pour forme régulière |
| Triangle | Polygones à 3 côtés | 3 convertir une chaîne en int java | 0 | 60° |
| Quadrilatère | Polygones à 4 côtés | 4 | 2 | 90° |
| Pentagone | Polygones à 5 côtés | 5 | 5 | 108° |
| Hexagone | Polygones à 6 côtés | 6 | 9 | 120° |
| Heptagone | Polygones à 7 côtés | 7 | 14 | 128,571° |
| Octogone | Polygones à 8 côtés | 8 | vingt | 135° |
| Nonagone | Polygones à 9 côtés programme d'héritage en python | 9 | 27 | 140° |
| Décagone | Polygones à 10 côtés | dix | 35 | 144° |
| Hendécagone | Polygones à 11 côtés | onze | 44 | 147,273° |
| Dodécagone | Polygones à 12 côtés | 12 | 54 | 150° |
Propriétés des polygones
Les propriétés des polygones les identifient facilement. Les propriétés suivantes contribuent à connaître facilement les polygones :
- Un polygone est une forme fermée, dépourvue d’extrémités ouvertes. L'origine et le point final doivent être identiques.
- Il prend une forme plane, composée de segments de lignes ou de lignes droites qui façonnent collectivement la figure.
- En tant qu'entité bidimensionnelle, un polygone n'existe que dans les dimensions de longueur et de largeur, sans profondeur ni hauteur.
- Il possède trois côtés ou plus pour former un polygone.
- Les angles dans le polygone peuvent varier. Il montre une configuration distincte.
- La longueur des côtés d'un polygone peut varier ; il peut ou non être le même dans tout le polygone.
Formes de polygones
Un polygone est une forme plate bidimensionnelle caractérisée par des côtés droits reliés pour former une figure fermée. Voici des exemples de formes de polygones :
- Triangle
- Quadrilatère
- Pentagone
- Hexagone
- Heptagone
- Octogone
- Nonagone
- Décagone
Triangle
- Il a 3 côtés et 3 sommets.
- Il n'a pas de diagonales.
- La somme de l'intérieur est de 180°.
Quadrilatère
- Il a 4 côtés et 4 sommets.
- Il a 2 diagonales.
- La somme des angles intérieurs est de 360°.
Pentagone
- Il a 5 côtés et 5 sommets.
- Il comporte 5 diagonales.
- La somme des angles intérieurs est de 540°.
Hexagone
- Il a 6 côtés et 6 sommets.
- Il comporte 9 diagonales.
- La somme des angles intérieurs est de 720°.
Heptagone
- Il a 7 côtés et 7 sommets.
- Il comporte 14 diagonales.
- La somme des angles intérieurs est de 900°.
Octogone
- Il a 8 côtés et 8 sommets.
- Il comporte 20 diagonales.
- La somme des angles intérieurs est de 1080°.
Nonagone
- Il a 9 côtés et 9 sommets.
- Il comporte 27 diagonales.
- La somme des angles intérieurs est de 1260°.
Décagone
- Il a 10 côtés et 10 sommets.
- Il comporte 35 diagonales.
- La somme des angles intérieurs est de 1440°.
Types de polygones
En fonction des côtés et des angles, les polygones peuvent être classés en différents types sur différentes bases telles que :
- Sur la base des côtés
- Sur la base des angles
- Sur la base des limites
Polygones sur la base des côtés
Les polygones peuvent être classés en fonction des caractéristiques de leurs côtés en deux types principaux :
- Polygone régulier
- Polygone irrégulier
Polygone régulier
Un polygone régulier se distingue par ses côtés de même longueur et tous ses angles intérieurs de mesures égales. Il peut être à la fois équilatéral et équiangulaire. Des exemples de polygones réguliers incluent le triangle, le quadrilatère, le pentagone et l'hexagone.

Polygone régulier
Polygone irrégulier
Un polygone irrégulier a des côtés de longueur inégale et des angles de mesures variables. Tout polygone qui ne répond pas aux critères d'un polygone régulier est classé comme irrégulier. Des exemples courants de polygones irréguliers sont le triangle scalène, les quadrilatères comme le rectangle, le trapèze ou le cerf-volant, ainsi que les structures irrégulières de pentagone et d'hexagone.
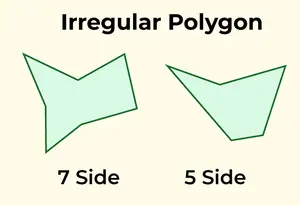
Polygone irrégulier
Polygones sur la base des angles
Les polygones peuvent être classés en fonction de la nature de leurs angles en deux catégories principales :
- Polygone convexe
- Polygone concave
Polygone convexe
Un polygone convexe n’a pas d’angle intérieur mesurant plus de 180°. Les polygones convexes peuvent avoir trois côtés ou plus. Dans les polygones convexes, toutes les diagonales se trouvent à l’intérieur de la figure fermée. Des exemples courants de polygones convexes sont les triangles, tous les quadrilatères convexes, ainsi que les pentagones et hexagones réguliers.
Polygone concave
Un polygone concave a au moins un angle intérieur qui est un angle réflexe et pointe vers l'intérieur. Les polygones concaves ont au moins quatre côtés. Ce type de polygone présente au moins un angle intérieur mesurant plus de 180°. Dans les polygones concaves, certaines diagonales s'étendent à l'extérieur de la figure ci-jointe. Des exemples de polygones concaves incluent une fléchette ou une pointe de flèche en quadrilatères, ainsi que certains pentagones et hexagones irréguliers.
Différence entre les polygones concaves et convexes
Voyons la différence entre les polygones convexes et concaves dans le tableau ci-dessous :

| Polygone convexe | Polygone concave |
|---|---|
| Tout le périmètre d’une forme convexe s’étend vers l’extérieur sans aucune indentation vers l’intérieur. | Une forme concave comporte au moins une partie pointant vers l’intérieur, indiquant la présence d’une bosse. |
| Dans un polygone convexe, tous les angles internes sont inférieurs à 180°. | Dans un polygone concave, il existe au moins un angle intérieur supérieur à 180°. |
| Toute ligne reliant deux sommets d’une forme convexe se trouve entièrement à l’intérieur des limites de la forme. Gimp enregistrant au format JPEG | La ligne reliant deux sommets quelconques d'une forme concave peut ou non couper l'intérieur de la forme. |
Polygones sur la base des limites
Les polygones peuvent être classés en fonction de la nature de leurs limites en deux types principaux :
- Polygone simple
- Polygone complexe
Polygone simple
Un polygone simple est caractérisé par une frontière singulière et sans intersection. En d’autres termes, il ne se traverse pas et consiste en une seule frontière.
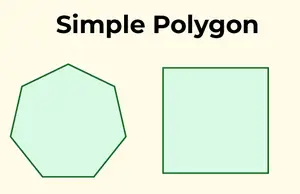
Polygones simples
Polygone complexe
D'un autre côté, un polygone complexe est défini par son intersection elle-même. Il se compose de plus d’une frontière au sein de sa structure. Dans les polygones complexes, les limites se croisent, créant plusieurs régions distinctes au sein du polygone.

Polygone complexe
En savoir plus sur Types de polygones.
Formules de polygones
Il existe plusieurs formules liées aux polygones en géométrie. Certains des plus couramment utilisés incluent :
- Formule de zone
- Formule de périmètre
- Nombre de diagonales
Toutes les formules liées aux différents polygones sont discutées ci-dessous :
Aire des polygones
Aire d'un polygone représente l’espace total qu’il occupe dans un plan bidimensionnel, est déterminé par des formules spécifiques basées sur le nombre de côtés et la classification du polygone. Les formules de superficie sont les suivantes :
| Aire du polygone | Formule |
|---|---|
| Aire du Triangle | 1/2 × Base × Hauteur |
| Aire du parallélogramme | Base × Hauteur |
| Aire d'un rectangle | Longueur × Largeur |
| Superficie du carré | (Côté)2 |
| 1/2 × diagonale1× diagonale2 | |
| Aire du trapèze | 1/2 × Hauteur × Somme des côtés parallèles |
| (5/2) × longueur du côté × Apothème | |
| Superficie de l'Hexagone | {(3√3)/2}côté2 |
| Aire de l'heptagone | 3,643 × Côté2 |
Périmètre des polygones
Le périmètre d'une forme bidimensionnelle représente la longueur totale de sa limite extérieure. Pour les polygones, le périmètre est calculé comme suit :
| Périmètre du polygone | Formule |
|---|---|
| Périmètre du Triangle | Somme de trois côtés |
| Périmètre du parallélogramme | 2 (Somme des côtés adjacents) |
| Périmètre du rectangle | 2(longueur + largeur) |
| Périmètre du carré | 4 × Côté |
| Périmètre du Losange | 4 × Côté |
| Périmètre du trapèze | Somme des côtés parallèles + Somme des côtés non parallèles |
| Périmètre du Pentagone | 5 × Côté |
| Périmètre de l'Hexagone | 6 × Côté polymorphisme |
| Périmètre de l'Heptagone | 7 × Côté |
Diagonale de la formule du polygone
Une diagonale d'un polygone est un segment de ligne formé en reliant deux sommets qui ne sont pas adjacents.
Nombre de diagonales dans un polygone = n(n−3)/2,
Où « n » représente le nombre de côtés que possède le polygone.
En savoir plus sur Diagonale de la formule du polygone .
Angles dans les polygones
En géométrie, les angles dans les polygones font référence aux angles formés par les côtés d'un polygone, à la fois à l'intérieur et à l'extérieur du polygone. Ainsi, il peut y avoir les deux angles dans un polygone, c'est-à-dire
- Angles intérieurs
- Angles extérieurs
Discutons en détail de la formule de ces angles comme suit :
Formule d'angle intérieur des polygones
Les angles intérieurs d'un polygone sont ceux formés entre ses côtés adjacents et sont égaux dans le cas d'un polygone régulier. Le nombre d'angles intérieurs correspond au nombre de côtés du polygone.
La somme des angles intérieurs « S » dans un polygone à « n » côtés est calculée comme suit :
S = (n – 2) × 180°
Où « n » représente le nombre de côtés.
Formule d'angle extérieur des polygones
Chaque angle extérieur d'un polygone régulier est formé en prolongeant l'un de ses côtés (dans le sens des aiguilles d'une montre ou dans le sens inverse) et en mesurant l'angle entre cette extension et le côté adjacent. Dans un polygone régulier, tous les angles extérieurs sont égaux
La somme totale des angles extérieurs dans n'importe quel polygone est fixée à 360°
Donc,
Chaque angle extérieur est donné par 360°/n
Où « n » est le nombre de côtés.
La somme des angles intérieurs et extérieurs correspondants à n'importe quel sommet d'un polygone est toujours de 180 degrés, exprimant une relation supplémentaire :
Angle intérieur + Angle extérieur = 180°
Angle extérieur = 180° – Angle intérieur
Conclusion
- Le polygone est une figure fermée délimitée par trois segments de ligne ou plus
- Somme des angles intérieurs : La somme de tous les angles intérieurs dans un polygone à n côtés est donnée par la formule (n – 2)×180°.
- Nombre de diagonales : Pour un polygone à n côtés, le nombre de diagonales est calculé à l'aide de la formule n(n–3)/2.
- Triangles formés par des diagonales : Le nombre de triangles formés en joignant les diagonales d’un seul coin d’un polygone est n–2.
- Angle intérieur du polygone régulier : La mesure de chaque angle intérieur dans un polygone régulier à n côtés est {(n–2)×180°}/n.
- Angle extérieur du polygone régulier : La mesure de chaque angle extérieur dans un polygone régulier à n côtés est de 360°/n.
Lisez également
- Carré
- Parallélogramme
- Rectangle
Exemples résolus sur les polygones en mathématiques
Exemple 1 : Considérons un quadrilatère à quatre côtés. Trouvez la somme de tous ses angles intérieurs du quadrilatère.
Solution:
Formule pour la somme des angles intérieurs dans un polygone régulier à n côtés = (n − 2) × 180°
La somme de tous les angles intérieurs du quadrilatère = (4 – 2) × 180°
La somme de tous les angles intérieurs du quadrilatère = 2 × 180°
La somme de tous les angles intérieurs du quadrilatère = 360°
La somme de tous les angles intérieurs du quadrilatère vaut donc 360°.
Exemple 2 : Considérons un polygone régulier avec un rapport d'angle extérieur et intérieur donné de 7:3. Déterminez le type de polygone.
Solution:
Le rapport entre l’angle extérieur et intérieur est de 7:3.
Supposons que l'angle extérieur et intérieur d'un polygone soit 7x et 3x.
La somme des angles extérieurs et intérieurs de tout polygone est de 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Angle extérieur = 18°
Nombre de côtés = 360°/angle extérieur
= 360°/18°
erreur d'attribut python= 20
Par conséquent, le polygone donné est un icosagone, car il a 20 côtés.
Exemple 3 : Chaque angle extérieur d'un polygone mesure 90 degrés, déterminez le type de polygone ?
Solution:
Selon la formule, chaque angle extérieur = 360°/n
Ici n = nombre de côtés.
90°= 360°/n
n = 360°/90°= 4
Le polygone en question est donc un quadrilatère, car il possède quatre côtés.
Exemple 4 : Les côtés font 10m, 10m, 8m, 8m, 5m, 5m, 9m, 9m. Combien de mètres de corde seront nécessaires pour le périmètre ?
Solution:
Afin de trouver la longueur de corde nécessaire pour le périmètre, il faut additionner les longueurs de tous les côtés :
Périmètre = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Périmètre = 64 m.
Un total de 64 mètres de corde sera donc nécessaire pour le périmètre.
Questions pratiques sur les polygones en géométrie
Voici quelques questions pratiques basées sur la formule des polygones :
T1. Étant donné qu'un angle d'un pentagone est de 140°, déterminez la taille du plus grand angle si les angles restants sont dans le rapport 1:2:3:4.
Q2. Si la somme des angles intérieurs d'un polygone est de 160°, trouvez le nombre de côtés du polygone.
Q3. Le nombre de côtés de deux polygones réguliers est dans le rapport 2:3 et le rapport de leurs angles intérieurs est 4:5. Trouvez les nombres respectifs de côtés de ces polygones.
Q4. Déterminez la somme totale des angles dans un heptagone.
Q5. Calculez la somme des angles extérieurs dans un pentagone.
Q6. Combien de côtés a un hexagone ?
- 4
- 6
- 8
- dix
Q7. Lequel des éléments suivants n’est pas un polygone régulier ?
- Triangle
- Carré
- Pentagone
- Parallélogramme
FAQ sur les polygones en mathématiques
Qu’est-ce qu’un polygone en mathématiques ?
En mathématiques, un polygone fait référence à une figure bidimensionnelle fermée formée par la connexion de trois lignes droites ou plus. Le terme polygone est dérivé de la langue grecque, poly- signifiant plusieurs et gon représentant un angle.
Quel est le plus petit polygone ?
Le plus petit polygone formé est un triangle à trois côtés.
Qu'est-ce que 20-gon ?
Un 20-gon est un polygone à vingt côtés en géométrie.
Quelle est la somme totale des angles externes du polygone ?
La somme des angles extérieurs d'un polygone est de 360°.
Un cercle peut-il être classé comme polygone ?
Le polygone est une forme fermée composée de segments de ligne droite. Le cercle est une figure fermée, mais il est constitué d’une courbe. Un cercle n’est donc pas un polygone.
Quelle est la somme des angles intérieurs d’un polygone ?
La somme de l'angle intérieur d'un polygone est donnée par (n – 2) × 180 ° où n est le nombre de côtés du polygone.
