Des portes logiques sont les composants fondamentaux de tous les circuits et systèmes numériques. En électronique numérique, il existe sept principaux types de portes logiques utilisé pour effectuer diverses opérations logiques. Une porte logique est essentiellement un circuit électronique conçu en utilisant des composants tels que des diodes, des transistors, des résistances, des condensateurs , etc., et capable d'effectuer des opérations logiques. Dans cet article, nous étudierons la définition, la table de vérité et d'autres concepts connexes des portes logiques. Commençons donc par l’introduction de base des portes logiques.
Table des matières
- Qu'est-ce qu'une porte logique ?
- Types de portes logiques
- ET Porte
- OU Porte
- PAS de porte
- Porte NI
- Porte NAND
- Porte XOR
- Porte XNOR
- Applications des portes logiques
Qu'est-ce qu'une porte logique ?
UN porte logique est un circuit électronique conçu à l'aide de composants électroniques tels que des diodes, des transistors, des résistances, etc. Comme son nom l'indique, une porte logique est conçue pour effectuer des opérations logiques dans des systèmes numériques tels que des ordinateurs, des systèmes de communication, etc.
Par conséquent, nous pouvons dire que les éléments constitutifs d’un circuit numérique sont des portes logiques, qui exécutent de nombreuses opérations logiques requises par tout circuit numérique. Une porte logique peut prendre deux entrées ou plus mais ne produire qu'une seule sortie. La sortie d'une porte logique dépend de la combinaison d'entrées et de l'opération logique effectuée par la porte logique.
Utilisation des portes logiques Algèbre de Boole pour exécuter des processus logiques. Les portes logiques se trouvent dans presque tous les gadgets numériques que nous utilisons régulièrement. Les portes logiques sont utilisées dans l'architecture de nos téléphones, ordinateurs portables, tablettes et périphériques de mémoire.
Types de portes logiques
Une porte logique est une porte numérique qui permet de manipuler des données. Les portes logiques utilisent la logique pour déterminer si un signal doit ou non être transmis. Les portes logiques, quant à elles, régissent le flux d’informations sur la base d’un ensemble de règles.
Les portes logiques peuvent être classées dans les principaux types suivants :
1. Portes logiques de base
Il existe trois portes logiques de base :
- ET Porte
- OU Porte
- PAS de porte
2. Portes logiques universelles
En électronique numérique, les deux portes logiques suivantes sont considérées comme des portes logiques universelles :
- Porte NI
- Porte NAND
3. Portes logiques dérivées
Les deux portes logiques suivantes sont utilisées dans les systèmes numériques :
- Porte XOR
- Porte XNOR
Discutons maintenant en détail de chacun de ces types de portes logiques, un par un.
ET Porte
En électronique numérique, la porte ET est l'une des portes logiques de base qui effectue la multiplication logique des entrées qui lui sont appliquées. Il génère une sortie haute ou logique 1, uniquement lorsque toutes les entrées qui lui sont appliquées sont hautes ou logique 1. Sinon, la sortie de la porte ET est basse ou logique 0.
Propriétés de la porte ET :
Voici deux propriétés principales de la porte ET :
- La porte ET peut accepter deux ou plus de deux valeurs d'entrée à la fois.
- Lorsque toutes les entrées sont à 1 logique, la sortie de cette porte est à 1 logique.
Le fonctionnement d'une porte ET est décrit par une expression mathématique, appelée expression booléenne de la porte ET.
Pour la porte ET à deux entrées, l'expression booléenne est donnée par,
Z = A.B
Où A et B sont les entrées de la porte ET, tandis que Z désigne la sortie de la porte ET.
Nous pouvons étendre cette expression à n'importe quel nombre de variables d'entrée, telles que :
Z=A.B.C.D…
Table de vérité de la porte ET :
La table de vérité d’une porte ET à deux entrées est donnée ci-dessous :
Saisir | Sortir | |
|---|---|---|
UN Excel supprimer le premier caractère | B | A ET B |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Symbole de la porte ET :
Le symbole logique d'une porte ET à deux entrées est illustré dans la figure suivante.
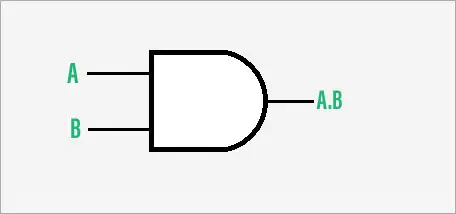
Symbole de la porte ET à deux entrées
OU Porte
En électronique numérique, il existe un type de porte logique de base qui produit une sortie basse ou logique 0 uniquement lorsque toutes ses entrées sont basses ou logiques 0. Pour toutes les autres combinaisons d'entrées, la sortie de la porte OU est haute ou logique 1. Ceci la porte logique est appelée porte OU. Une porte OU peut être conçue pour avoir deux entrées ou plus mais une seule sortie. La fonction principale de la porte OU est d’effectuer l’opération de somme logique.
Propriétés de la porte OU :
Une porte OU possède les deux propriétés suivantes :
- Il peut avoir deux lignes d'entrée ou plus à la fois.
- Lorsque toutes les entrées de la porte OU sont faibles ou logiques 0, la sortie de celle-ci est faible ou logique 0.
Le fonctionnement d'une porte OU peut être décrit mathématiquement au moyen d'une expression mathématique appelée expression booléenne de la porte OU.
L'expression booléenne pour une porte OU à deux entrées est donnée par,
Z = A + B
L'expression booléenne d'une porte OU à trois entrées est :
Z = A + B + C
Ici, A, B et C sont des entrées et Z sont les variables de sortie. Nous pouvons étendre cette expression booléenne à n'importe quel nombre de variables d'entrée.
Table de vérité de la porte OU :
La table de vérité d'une porte OU décrit la relation entre les entrées et la sortie. Voici la table de vérité de la porte OU à deux entrées :
Saisir | Sortir | |
|---|---|---|
UN | B | A OU B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Symbole de la porte OU :
Le symbole logique d'une porte OU à deux entrées est illustré dans la figure suivante.

Symbole de la porte OU à deux entrées
PAS de porte
En électronique numérique, la porte NON est une autre porte logique de base utilisée pour effectuer complément d'un signal d'entrée appliqué à celui-ci. Cela ne prend qu’une seule entrée et une seule sortie. La sortie de la porte NON est complémentaire de l’entrée qui lui est appliquée. Par conséquent, si nous appliquons une sortie basse ou logique 0 à la porte NON, cela donne une sortie haute ou logique 1 et vice versa. La porte NON est également appelée inverseur, car elle effectue l'opération d'inversion.
Propriétés de NOT Gate :
- La sortie d'une porte NON est complémentaire ou inverse de l'entrée qui lui est appliquée.
- La porte NOT ne prend qu'une seule sortie.
Le fonctionnement logique de la porte NON est décrit par son expression booléenne, donnée ci-dessous.
Z= overline{A}
La barre au-dessus de la variable d'entrée A représente l'opération d'inversion.
Table de vérité de la porte OU :
La table de vérité décrit la relation entre l'entrée et la sortie. Voici la table de vérité de la porte NON :
Saisir | Sortir |
|---|---|
UN | PAS UN |
0 | 1 |
1 | 0 |
Symbole de NOT Gate
Le symbole du circuit logique d'une porte NON est illustré dans la figure suivante. Ici, A est la ligne d’entrée et Z est la ligne de sortie.

Symbole de PAS la porte
Porte NI
La porte NOR est un type de porte logique universelle qui peut prendre deux entrées ou plus mais une sortie. Il s'agit essentiellement d'une combinaison de deux portes logiques de base, à savoir la porte OU et la porte NON. Ainsi, cela peut être exprimé comme suit:
Porte NI = Porte OU + Porte NON
En d’autres termes, une porte NOR est une porte OU suivie d’une porte NON.
Propriétés de la porte NOR :
Voici deux propriétés importantes de la porte NOR :
chaîne.replaceall en java
- Une porte NOR peut avoir deux entrées ou plus et donne une sortie.
- Une porte NOR donne une sortie haute ou logique 1 uniquement lorsque toutes ses entrées sont basses ou logiques 0.
Semblable aux portes logiques de base, nous pouvons décrire le fonctionnement d’une porte NON-OU à l’aide d’une équation mathématique appelée expression booléenne de la porte NON-OU.
L’expression booléenne d’une porte NON-OU à deux entrées est donnée ci-dessous :
C=overline{A+B}
Nous pouvons étendre cette expression à n’importe quel nombre de variables d’entrée.
Dans les expressions booléennes ci-dessus, les variables A et B sont appelées variables d'entrée tandis que la variable C est appelée variable de sortie.
Table de vérité de la porte NOR :
Ce qui suit est la table de vérité d'une porte NON-OU à deux entrées montrant la relation entre ses entrées et sa sortie :
Saisir | Sortir | |
|---|---|---|
UN | B | A NI B |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |

Symbole de la porte NOR
Porte NAND
En électronique numérique, la porte NAND est un autre type de porte logique universelle utilisée pour effectuer des opérations logiques. La porte NAND effectue le fonctionnement inversé de la porte ET. Semblable à la porte NOR, la porte NAND peut également avoir deux lignes d'entrée ou plus mais une seule ligne de sortie.
La porte NAND est également représentée comme une combinaison de deux portes logiques de base, à savoir la porte ET et la porte NON. On peut donc l’exprimer sous la forme
Porte NAND = Porte ET + Porte NON
Propriétés de la porte NAND :
Voici les deux propriétés clés de la porte NAND :
méthode java
- La porte NAND peut prendre deux entrées ou plus à la fois et produit une sortie basée sur la combinaison d'entrées appliquée.
- La porte NAND produit une sortie faible ou logique 0 uniquement lorsque toutes ses entrées sont élevées ou logiques 1.
Nous pouvons décrire l'expression de la porte NAND à travers une équation mathématique appelée son expression booléenne. Voici l'expression booléenne d'une porte NAND à deux entrées.
C=overline{AB}
Dans cette expression, A et B sont les variables d’entrée et C est la variable de sortie. Nous pouvons étendre cette relation à n'importe quel nombre de variables d'entrée comme trois, quatre ou plus.
Table de vérité de la porte NAND :
La table de vérité est un tableau d'entrées et de sorties qui décrit le fonctionnement de la porte NAND et montre la relation logique entre elles :
Saisir | Sortir | |
|---|---|---|
UN | B | UNE NAND B |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Symbole de la porte NAND :
Le symbole logique d'une porte NAND est représenté comme une porte ET avec une bulle à son extrémité de sortie, comme illustré dans la figure suivante. C'est le symbole d'une porte NAND à deux entrées.

Symbole de la porte NAND
Porte XOR
En électronique numérique, il existe une porte logique spécialement conçue appelée porte XOR, qui est utilisée dans les circuits numériques pour effectuer module de somme . On l'appelle également Porte OU exclusive ou porte Ex-OU . La porte XOR ne peut prendre que deux entrées à la fois et donner une sortie. La sortie de la porte XOR est haute ou logique 1 uniquement lorsque ses deux entrées sont différentes.
Propriétés de la porte XOR :
Les deux propriétés suivantes sont les principales propriétés de la porte XOR :
- Il ne peut accepter que deux entrées à la fois. Il n’y a rien de tel qu’une porte XOR à trois entrées ou plus.
- La sortie de la porte XOR est logique 1 ou élevée, lorsque ses entrées sont différentes.
Le fonctionnement de la porte XOR peut être décrit à travers une équation mathématique appelée expression booléenne. Ce qui suit est l'expression booléenne de la sortie de la porte XOR.
Z=A oplus B
Ici, Z est la variable de sortie et A et B sont les variables d'entrée.
Cette expression peut également s’écrire ainsi :
Z=A overline{B}+overline{A}B
Table de vérité de la porte XOR :
La table de vérité est un tableau d'entrées et de sorties qui décrit la relation entre elles et le fonctionnement de la porte XOR pour différentes combinaisons d'entrées. La table de vérité de la porte XOR est donnée ci-dessous :
Saisir | Sortir | |
|---|---|---|
UN | B | A XOR B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Symbole de la porte XOR :
Le symbole logique d'une porte XOR est illustré dans la figure suivante.

Symbole de la porte XOR
Porte XNOR
La porte XNOR est un autre type de porte logique spéciale utilisée pour mettre en œuvre fonctionnement exclusif dans les circuits numériques . Il est utilisé pour implémenter l’opération NOR exclusif dans les circuits numériques. Elle est également appelée porte Ex-NOR ou Exclusive NOR. Il s'agit d'une combinaison de deux portes logiques, à savoir la porte XOR et la porte NOT. Ainsi, cela peut être exprimé comme suit:
java sinon
Porte XNOR = Porte XOR + Porte NON
La sortie d'une porte XNOR est haute ou logique 1 lorsque ses deux entrées sont similaires. Sinon, la sortie est faible ou logique 0. Par conséquent, la porte XNOR est utilisée comme circuit détecteur de similarité.
Propriétés de la porte XNOR :
Voici deux propriétés clés de la porte XNOR :
- La porte XNOR ne prend que deux entrées et produit une sortie.
- La sortie de la porte XNOR est haute ou logique 1 uniquement lorsqu'elle a des entrées similaires.
Le fonctionnement de la porte XNOR peut être décrit à travers une équation mathématique appelée expression booléenne de la porte XNOR. Voici l'expression booléenne de la porte XNOR.
Y=A odot B
On peut aussi écrire cette expression comme suit :
Y=AB + overline{A} overline{B}
Ici, A et B sont des entrées et Y est la sortie.
Table de vérité de XNOR Gate :
La table de vérité de la porte XNOR est donnée ci-dessous. Cette table de vérité décrit la relation entre les entrées et la sortie de la porte XNOR.
Saisir | Sortir | |
|---|---|---|
UN | B | A XNOR B |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Symbole de la porte XNOR :
Le symbole logique de la porte XNOR est illustré dans la figure suivante. Ici, A et B sont les entrées et Y est la sortie.

Symbole de la porte XNOR
Applications des portes logiques
Les portes logiques sont les éléments fondamentaux de tous les circuits et appareils numériques comme les ordinateurs. Voici quelques appareils numériques clés dans lesquels des portes logiques sont utilisées pour concevoir leurs circuits :
- Des ordinateurs
- Microprocesseurs
- Microcontrôleurs
- Montres numériques et intelligentes
- Smartphones, etc.
Basé sur des portes logiques – FAQ
Que sont les portes logiques ?
Les portes logiques sont des circuits numériques qui effectuent des opérations logiques sur l'entrée qui leur est fournie et produisent une sortie appropriée.
Que sont les portails universels ?
Pour accomplir un processus logique spécifique, les portes universelles sont créées en fusionnant deux ou plusieurs portes fondamentales. Les portes universelles sont des portes NAND et NOR.
Quelle est la sortie d’une porte NON lorsque l’entrée 0 est appliquée ?
Parce que NOT Gate est un onduleur. Par conséquent, si 0 est utilisé comme entrée, la sortie sera 1.
Quelle porte logique est connue sous le nom d’inverseur ?
Un inverseur est également appelé porte NON. La sortie obtenue est l’inverse de l’entrée.
Quelle est l’expression booléenne de la porte OU ?
Si A et B sont les entrées, alors la sortie de la porte OU peut être donnée comme Y=A+B.
Quelle est l’expression booléenne de la porte XNOR ?
Si A et B sont les entrées, alors la sortie de la porte XNOR peut être donnée comme Y=A.B+A'B'.
