Axe de symétrie: Une ligne de symétrie, également appelée axe de symétrie ou ligne miroir, est une ligne qui divise une forme ou un objet en deux moitiés identiques et symétriques. Chaque moitié reflète l'autre, ce qui les fait ressembler à des reflets l'un de l'autre sur la ligne, ce qui indique que les deux parties de la forme correspondraient parfaitement. La forme ne changerait pas si un miroir était placé le long de cette ligne.
Dans cet article, nous parlerons du concept de axe de symétrie, ainsi que sa définition et ses propriétés. Nous explorerons également les lignes de symétrie dans les alphabets et les lignes de symétrie dans des formes comme le Triangle, le Losange, le Parallélogramme, le Pentagone, etc.
Table des matières
- Qu’est-ce que l’axe de symétrie ?
- Propriétés de l'axe de symétrie
- Types de lignes de symétrie
- Ligne de symétrie pour différentes formes
- Ligne de symétrie en triangle
- Ligne de symétrie dans le quadrilatère
- Ligne de symétrie dans le trapèze (pas de lignes de symétrie)
- Ligne de symétrie en parallélogramme (pas de lignes de symétrie)
- Ligne de symétrie dans Kite (symétrie à une ligne)
- Ligne de symétrie dans un rectangle (symétrie à deux lignes)
- Ligne de symétrie en losange (symétrie à deux lignes)
- Ligne de symétrie dans un carré (symétrie à quatre lignes)
- Ligne de symétrie dans les polygones supérieurs
- Ligne de symétrie au Pentagone (symétrie à cinq lignes)
- Ligne de symétrie en hexagone (symétrie à six lignes)
- Ligne de symétrie en heptagone (symétrie à sept lignes)
- Ligne de symétrie en octogone (symétrie à huit lignes)
- Ligne de symétrie dans d'autres formes
- Ligne de symétrie dans les alphabets
- Ligne verticale de symétrie dans les alphabets anglais
- Ligne horizontale de symétrie dans les alphabets anglais
- Deux lignes de symétrie (horizontales et verticales) dans les alphabets anglais
- Ligne zéro de symétrie dans les alphabets anglais
- Équations de ligne de symétrie
- Exemples d'axe de symétrie
- Questions pratiques sur l'axe de symétrie
Qu’est-ce que l’axe de symétrie ?
Une ligne de symétrie est une ligne imaginaire qui divise ou sépare une forme ou un objet en moitiés symétriques. En termes simples, une moitié est le reflet de l’autre moitié.
Dans le Taj Mahal, nous observons que la moitié d’un côté du Taj Mahal est la même que la moitié de l’autre côté, car chaque côté est un reflet parfait ou une image miroir de l’autre côté.
Si vous coupez un objet le long de son axe, cela créera un reflet semblable à un miroir de chaque côté de l'objet. Cet axe est appelé axe de symétrie. Par exemple, si nous coupons des étoiles de mer et des poulpes le long de leur axe de symétrie, nous obtiendrons des formes similaires.
Signification de l’axe de symétrie
Un axe de symétrie est une ligne qui divise un objet en deux parties égales. Ces deux parties sont le reflet miroir l’une de l’autre. Une ligne de symétrie est une ligne imaginaire qui passe par le centre de cet objet.
Propriétés de l'axe de symétrie
Il existe quelques propriétés pour comprendre efficacement la notion d’axe de symétrie :
- Si un corps ne contient aucune ligne de symétrie, alors ce corps implique une asymétrie.
- Une forme ou un corps peut avoir des lignes de symétrie infinies. Par exemple, en rond.
- Un objet peut avoir une ligne de symétrie. Par exemple, les ailes d’un papillon n’ont qu’une seule ligne de symétrie le long de son axe vertical.
- Certains objets peuvent avoir deux lignes de symétrie.
Vérifier: Symétrie
Types de lignes de symétrie
Généralement, trois types d’axes de symétrie peuvent être observés dans différentes figures géométriques :
- Ligne de symétrie horizontale
- Ligne verticale de symétrie
- Ligne diagonale de symétrie
Ligne horizontale de symétrie
La ligne de symétrie horizontale est une ligne droite endormie qui divise une forme géométrique en deux moitiés égales de manière horizontale. Cela va de gauche à droite ou de droite à gauche dans un objet.
Ligne verticale de symétrie
La ligne de symétrie verticale est une ligne droite debout qui divise une forme géométrique en deux moitiés égales de manière verticale. Cela va de haut en bas ou vice versa dans un objet.
Ligne diagonale de symétrie
La ligne de symétrie diagonale est une ligne inclinée qui divise une forme géométrique en deux moitiés égales sur le côté.
Ligne de symétrie pour différentes formes
En géométrie, nous avons des formes avec une ou plusieurs lignes de symétrie selon sa structure comme le carré, le rectangle, le triangle, le losange et le parallélogramme. Ces lignes peuvent être horizontales, verticales ou diagonales. Dans les formes bidimensionnelles, nous apprendrons les lignes de symétrie pour suivre les formes
- Ligne de symétrie en triangle
- Ligne de symétrie dans le quadrilatère
- Ligne de symétrie dans d'autres polygones
- Ligne de symétrie dans d'autres formes
Ligne de symétrie en triangle
Un triangle est un polygone délimité par des segments de trois lignes. En fonction de la longueur des côtés, il existe trois types de triangles, à savoir le triangle équilatéral, le triangle isocèle et Triangle scalène.
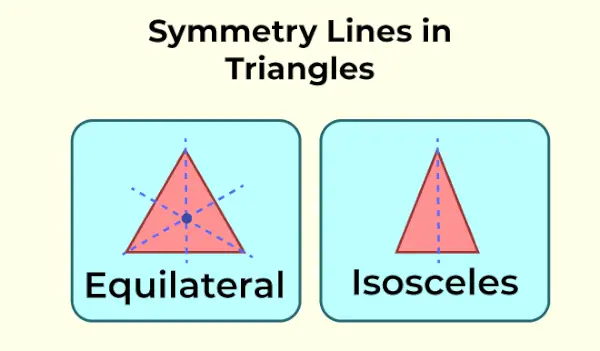
Ligne de symétrie dans un triangle équilatéral (symétrie à trois lignes)
Un triangle équilatéral est un triangle dont tous les côtés sont égaux. Par conséquent, un triangle équilatéral a trois axes de symétrie. Les lignes de symétrie partent du sommet et du milieu du côté opposé.
Ligne de symétrie dans un triangle isocèle (symétrie à une ligne)
Le triangle isocèle est un triangle dont seuls deux côtés sont égaux. Par conséquent, un triangle isocèle n’a qu’un seul axe de symétrie.
qui a créé l'école
Ligne de symétrie dans le triangle scalène (pas de lignes de symétrie)
UN triangle scalène est un triangle dans lequel aucun côté n’est égal. Par conséquent, le triangle scalène n’a pas d’axes de symétrie.
Ligne de symétrie dans le quadrilatère
Un quadrilatère est un polygone qui possède quatre côtés. Les différents types de quadrilatère sont le trapèze, le parallélogramme, le losange, le carré, le rectangle et le cerf-volant. Découvrons les lignes de symétrie dans différents quadrilatères.

Ligne de symétrie dans le trapèze (pas de lignes de symétrie)
UN trapèze est un quadrilatère dont deux côtés opposés sont parallèles. Un trapèze n'a pas de lignes de symétrie.
Ligne de symétrie en parallélogramme (pas de lignes de symétrie)
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles et égaux. Un parllélogramme n’a pas d’axes de symétrie.
Ligne de symétrie dans Kite (symétrie à une ligne)
Un cerf-volant contient une ligne de symétrie. Cette ligne de symétrie du cerf-volant est de nature verticale.
Ligne de symétrie dans un rectangle (symétrie à deux lignes)
Un rectangle a deux lignes de symétrie : une verticale et une horizontale. Ces lignes passent par les milieux des côtés opposés. Lorsqu'il est plié en diagonale, il donne une forme asymétrique.
Ligne de symétrie en losange (symétrie à deux lignes)
UN rhombe a deux lignes de symétrie. Ces deux axes de symétrie du losange sont ses diagonales.
Ligne de symétrie dans un carré (symétrie à quatre lignes)
Un carré a quatre lignes de symétrie : une verticale, une horizontale et deux lignes de symétrie diagonales. Les quatre axes de symétrie sont formés par des lignes passant par les milieux des côtés opposés.
Ligne de symétrie dans les polygones supérieurs
Nous savons qu'un polygone est une figure fermée délimitée par trois segments de ligne ou plus. Ci-dessus, nous avons découvert les axes de symétrie des triangles et des quadrilatères. Apprenons les lignes de symétrie dans les polygones supérieurs tels que le pentagone, l'hexagone, etc.

Ligne de symétrie au Pentagone (symétrie à cinq lignes)
Un habitué Pentagone a cinq lignes de symétrie : une horizontale, une verticale et trois diagonales.
Ligne de symétrie en hexagone (symétrie à six lignes)
Un hexagone régulier contient six lignes de symétrie : une horizontale, une verticale et quatre diagonales.
Ligne de symétrie en heptagone (symétrie à sept lignes)
Un heptagone régulier possède 7 côtés égaux. Il y a donc 7 axes de symétrie dans Heptagone.
Ligne de symétrie en octogone (symétrie à huit lignes)
Un octogone contient huit lignes de symétrie. Sur ces 8 lignes de symétrie, quatre sont des lignes de symétrie horizontales et quatre sont des lignes de symétrie verticales.
Ligne de symétrie dans d'autres formes
Dans cette rubrique, nous apprenons les lignes de symétrie pour d'autres formes telles que le cercle et l'étoile. Puisqu’un cercle peut se plier le long des lignes de diamètre, toutes les lignes de symétrie d’un cercle seront donc le long de son diamètre. Dans le cas d’une étoile, les lignes de symétrie sont le long des lignes joignant les sommets opposés.

Ligne de symétrie en cercle (lignes de symétrie infinies)
Un cercle a un nombre infini de lignes de symétrie car il est symétrique le long de son axe infini et un nombre infini de lignes peuvent passer par son centre.
Ligne de symétrie en étoile (symétrie à cinq lignes)
Dans Star, les lignes de symétrie passent par les sommets opposés. Par conséquent, dans une étoile, il y a au total cinq axes de symétrie.
Ligne de symétrie dans les alphabets
Outre les formes géométriques, les alphabets anglais comportent également des lignes de symétrie. Les sujets mentionnés ci-dessous expliquent les lignes de symétrie dans les alphabets anglais.

pas nul en js
Ligne verticale de symétrie dans les alphabets anglais
Les alphabets anglais par rapport à l'axe de symétrie vertical sont A, H, I, M, O, T, U, V, W, X, Y.
Ligne horizontale de symétrie dans les alphabets anglais
Les alphabets anglais par rapport à la ligne horizontale de symétrie sont B, C, D, E, H, I, K, O, X.
Deux lignes de symétrie (horizontales et verticales) dans les alphabets anglais
Les lettres qui ont des lignes de symétrie horizontales et verticales sont H, I , O , X.
Ligne zéro de symétrie dans les alphabets anglais
Les alphabets tels que F, G, L, P, Q, R, S, Z n'ont pas d'axe de symétrie.
Équations de ligne de symétrie
Il existe plusieurs façons de trouver l’axe de symétrie. Dans le système de coordonnées, le graphique peut avoir une symétrie par rapport à l'axe des x, à l'axe des y, à l'origine ou à toute ligne donnée.
Par exemple, une parabole a une symétrie linéaire en géométrie de coordonnées et une équation de symétrie linéaire pour une parabole avec l'équation quadratique y = ax2+ bx + c est de la forme x = n, où n est un nombre réel et a et b sont les coefficients de x2et x respectivement et c est la constante. x = -b/(2a) nous donne notre axe de symétrie.
Cela signifie que l'axe de symétrie est la ligne verticale passant par x = -b/(2a). Cette ligne divisera la parabole en deux moitiés égales.
Par exemple, si on nous donne l’équation d’une parabole sous forme standard telle que y = x2+ 6x + 3, on sait que a=1, b=6 et c=3. Ici, nous pouvons mettre la valeur de a et b dans la formule x=−b/2a afin d'obtenir l'axe de symétrie. La formule devient x =−(6)/2(1) ce qui donne x = −3. Cela signifie que l’axe de symétrie est la droite verticale passant par x=−3.
Les gens lisent également :
- Types de lignes
- Lignes et angles
- Lignes parallèles
Exemples d'axe de symétrie
Exemple 1. Trouver l'axe de symétrie de la parabole y = -2x 2 − 4x + 8.
Solution:
Équation donnée : y = -2x2−4x + 8
Comparez l'équation donnée avec la forme standard hache2+ bx + c.
⇒ une = -2, b = −4, c = 8
Utilisez la formule de l'axe de symétrie = −b/2a
= −(−4)/2(-2) ⇒x = 1
L'équation de la droite pour l'axe de symétrie est x=1.
Exemple 2. Trouver l'axe de symétrie de la parabole y = 4x 2 .
Solution:
Équation donnée : y = 4x2
Comparez l'équation donnée à la forme standard hache2+ bx + c.
⇒ une = 4, b = 0, c = 0
Utilisez la formule de l'axe de symétrie = −b/2a
= -0/2(4) ⇒x = 0
Exemple 3. Comment localiser les lignes de symétrie d’une forme ?
Solution:
Tout d’abord, nous allons plier la forme le long d’une ligne de telle sorte qu’une moitié soit exactement similaire à l’autre moitié. Cette ligne est connue sous le nom d’axe de symétrie.
Exemple 4. Combien de lignes de symétrie peut-on tracer sur un pentagone régulier ?
Solution:
Une ligne de symétrie divise une figure en deux images miroir identiques. Un total de 5 lignes de symétrie peuvent être tracées sur un pentagone régulier : une horizontale, une verticale et trois en diagonale.
Exemple 5. Quelle est la formule standard de l'axe de symétrie d'une parabole ?
Solution:
La formule standard de l'axe de symétrie d'une équation (y=ax2+ bx + c) est x = −b/2a
Questions pratiques sur l'axe de symétrie
T1. Tracez toutes les lignes de symétrie du triangle équilatéral.
Q2. Tracez toutes les lignes de symétrie du pentagone régulier.
Q3. Combien d’axes de symétrie peut-on tracer dans un cercle ?
Q4. Combien d’axes de symétrie peut-on tracer dans un triangle isocèle et un triangle scalène ?
Q5. Combien d’alphabets ont exactement deux axes de symétrie ?
Q6. Combien d’alphabets ont exactement un seul axe de symétrie ?
Q7. Écrivez l'axe de symétrie de l'équation quadratique y = x2+18x+8.
Ligne de symétrie – FAQ
Qu’est-ce que la symétrie en mathématiques ?
La symétrie en mathématiques est l'état d'avoir deux moitiés égales qui correspondent exactement en taille et en forme lorsqu'elles se divisent le long d'une ligne imaginaire.
Combien d’axes de symétrie possède un rectangle ?
Un rectangle a deux lignes de symétrie : une verticale et une horizontale.
Combien d’axes de symétrie possède un carré ?
Un carré a quatre lignes de symétrie : une verticale, une horizontale et deux lignes de symétrie diagonales.
Combien d’axes de symétrie possède un losange ?
Un losange a 2 axes de symétrie : deux diagonales.
Combien d’axes de symétrie possède un parallélogramme ?
Zéro ligne de symétrie.
Combien de lignes de symétrie possède un cerf-volant ?
Une seule ligne de symétrie : verticale.
Combien d’axes de symétrie possède une étoile ?
Une étoile à six étoiles a six axes de symétrie
Qu'est-ce que l'axe de symétrie ?
L'axe de symétrie est défini comme la ligne imaginaire le long de laquelle une figure ou une forme peut être pliée ou divisée en deux moitiés symétriques.
Combien de lignes de symétrie peuvent être tracées en demi-cercle ?
Une seule ligne symétrique peut être tracée en demi-cercle.
Combien de lignes de symétrie peuvent passer par un alphabet anglais H ?
Deux lignes de symétrie : une ligne horizontale et une ligne verticale peuvent passer par H.
Quel triangle n'a pas d'axe de symétrie ?
Le triangle scalène ne contient aucun axe de symétrie. C'est un triangle asymétrique.
Quelles formes n’ont pas de ligne de symétrie ?
Le triangle scalène, le trapèze, le parallélogramme, etc. n'ont pas d'axes de symétrie.
filtrage de Python
