La ligne est une forme géométrique unidimensionnelle dont les deux côtés s’étendent à l’infini. Il existe différents types de lignes en géométrie, en fonction de leur forme, de leur orientation et de leur intersection. Découvrons les différents types de lignes en géométrie et leurs applications en détail.
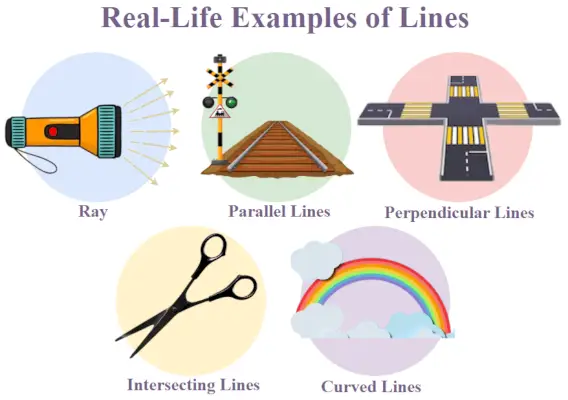
Table des matières
- Qu'est-ce que la ligne
- Types de lignes
- Ligne droite
- Types de lignes basées sur l'intersection
- Types spéciaux de lignes
- Axe de symétrie
Qu'est-ce que la ligne
Doubler est la combinaison de points infinis qui s’étendent à l’infini dans les deux directions. Il est défini comme une forme unidimensionnelle, ayant une longueur sans aucune largeur.
Il est généralement représenté par une ligne droite avec des pointes de flèches aux deux extrémités. La pointe de flèche représente l'extension indéfinie.
Qu'est-ce que Ray
Une ligne droite qui peut s’étendre à l’infini dans une direction et dont l’autre extrémité est fixe est appelée une rayon . Comme un rayon peut s’étendre à l’infini d’un côté. Il n'a pas de longueur définie.
Par exemple, si A est le point final et B est un point dans la direction du rayon, cela peut être noté rayon AB ou simplement rayon A .
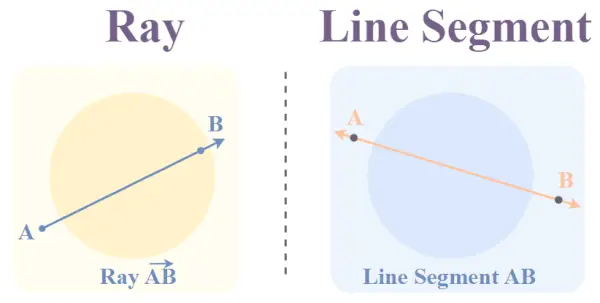
Illustration d'un rayon et d'un segment de ligne
Qu'est-ce qu'un segment de ligne
Les segments d'une ligne ayant deux extrémités sont appelés segments de ligne. En d’autres termes, un segment de ligne est une partie fractionnaire d’une ligne
Il est généralement représenté par deux points quelconques situés sur la ligne, chaque point portant un nom alphabétique. Par exemple, si deux extrémités de segments de droite sont A et B, alors le segment de droite peut s’écrire AB.
Types de lignes
Il existe différents types de lignes en géométrie, ayant différentes propriétés et caractéristiques.
- Types de lignes basées sur la structure
- Lignes droites
- Lignes courbes
- Lignes en zigzag
- Lignes brisées ou lignes pointillées
- Types de lignes basées sur l'orientation
- Lignes horizontales
- Lignes verticales
- Lignes diagonales
- Types de lignes basées sur l'intersection
- Lignes d'intersection
- Lignes bissectrices
- Les lignes perpendiculaire
- Lignes parallèles
- Lignes transversales
Types de lignes basées sur la forme
En fonction de la forme ou du changement de direction, nous pouvons classer les lignes comme suit :
- Lignes droites
- Lignes courbes
- Lignes en zigzag
- Lignes brisées ou lignes pointillées
Discutons-en en détail.
Ligne droite
Les lignes droites sont les lignes qui ne s'écartent pas d'un chemin linéaire même après s'être étendues jusqu'à l'infini. Ces lignes se caractérisent par le fait qu’elles ont la même direction et aucune courbure.
np.zéros
Nous pouvons prolonger indéfiniment des lignes droites dans les deux sens. Une ligne a la même pente constante (l’angle par rapport à l’axe des x positif).
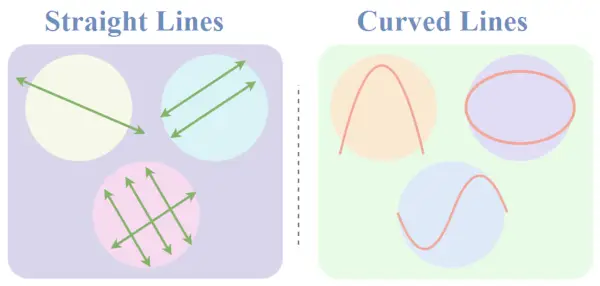
Illustration de lignes droites et de lignes courbes
Ligne courbe
Les lignes courbes sont ces lignes qui changent progressivement de direction. Leur pente évolue progressivement entre différentes valeurs. Contrairement aux lignes droites, elles ne suivent pas un chemin linéaire.
Les lignes courbes lorsqu'elles sont fermées peuvent former divers objets géométriques différents tels que des cercles et des ellipses, et lorsqu'elles ne sont pas fermées, elles créent une courbure comme des spirales, des arcs, des paraboles, etc.
Ligne en zigzag
Les lignes en zigzag sont des ensembles de segments de ligne très pointus dont la pente change soudainement. Ces lignes sont constituées d’une série de segments de ligne connectés qui ont une pente positive et négative dans un ordre alterné.
Ces lignes ressemblent à une séquence de formes Z ou N et forment une ligne irrégulière. Le principal cas d'utilisation des lignes en zigzag concerne l'art et le design graphique, où ces lignes sont utilisées pour représenter un changement rapide et soudain ou un mouvement dynamique.
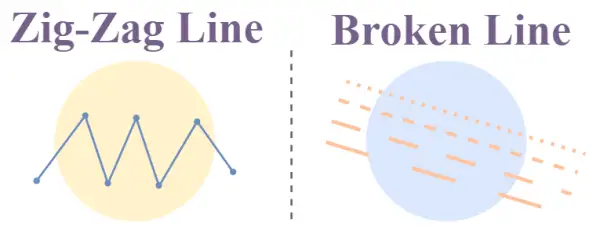
Illustration de zigzag et de lignes brisées
Ligne brisée
Les lignes brisées sont un ensemble de nombreux petits segments de ligne disposés en ligne droite, la longueur de chaque segment de ligne pouvant varier en fonction du cas d'utilisation.
On les appelle également lignes pointillées, car ces segments de ligne ressemblent à des tirets.
Types de lignes basées sur l'orientation
- Lignes horizontales
- Lignes verticales
- Lignes diagonales
Discutons-en en détail.
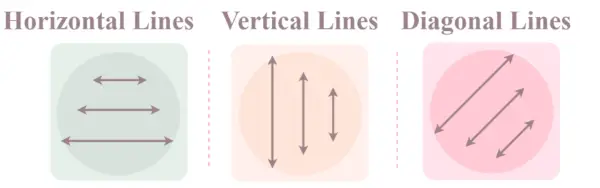
Types de lignes basées sur l'orientation
Ligne horizontale
Les lignes horizontales sont les lignes parallèles à l'axe horizontal, c'est-à-dire à l'axe des x ou au niveau du sol. En d’autres termes, les lignes qui vont de gauche à droite ou vice versa sont appelées lignes horizontales.
En algèbre, on peut représenter les lignes horizontales en utilisant l'équation y = constante.
Ligne verticale
Les lignes verticales sont à l’opposé des lignes horizontales et sont parallèles à l’axe vertical, c’est-à-dire à l’axe y. En d’autres termes, les lignes perpendiculaires au niveau du sol sont appelées lignes verticales.
Ces lignes vont de haut en bas et nous pouvons voir ces lignes dans le monde réel sous forme de poteaux, de bâtiments à plusieurs étages, de colonnes pour soutenir des structures, etc.
Ligne diagonale
Les lignes diagonales sont des lignes qui ne vont ni dans une direction horizontale ni dans une direction verticale car ces lignes sont inclinées dont la pente se situe entre l'horizontale et la verticale.
On les appelle aussi lignes obliques.
Types de lignes basées sur l'intersection
- Lignes d'intersection
- Lignes bissectrices
- Les lignes perpendiculaire
- Lignes parallèles
- Lignes transversales
Discutons-en en détail.
installer maven
Lignes d'intersection
Les lignes sécantes sont deux lignes ou plus qui se rencontrent, se croisent ou se croisent en un point commun. Le point de rencontre de ces lignes est appelé le point d'intersection.
En algèbre, ce point d'intersection est une solution du système d'équations formé par les deux droites.
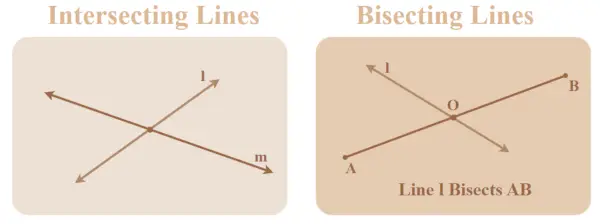
Illustration des lignes sécantes et bissectrices
Lignes bissectrices
Les lignes bissectrices sont les lignes qui divisent un segment de ligne en deux parties égales. Cet objet peut être un angle, un triangle, n'importe quel polygone ou un segment de ligne. Ils passent par le milieu de l'objet.
Les lignes bissectrices sont couramment utilisées en géométrie pour diviser des angles ou des segments de ligne de manière égale.
Les lignes perpendiculaire
Les lignes perpendiculaires sont des lignes qui se croisent et forment un angle droit entre elles. Une de ces paires de lignes perpendiculaires sont des lignes verticales et horizontales si elles se croisent. De plus, la pente des lignes perpendiculaires a une relation entre elles, c'est-à-dire que le produit de la pente des lignes perpendiculaires est toujours -1. Par exemple, si une ligne a une pente de 2, la ligne perpendiculaire aura une pente de -1/2.
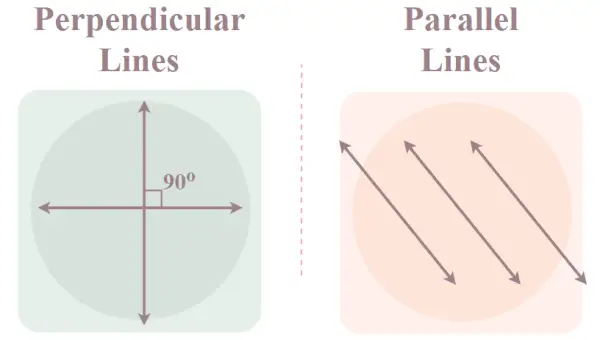
Représentation des lignes perpendiculaires et parallèles
Lire la suite sur :
Lignes parallèles
Les lignes parallèles sont à l’opposé des lignes qui se croisent, c’est-à-dire qu’elles ne se coupent jamais, quelle que soit leur extension. Toutes les droites parallèles ont la même pente mais des ordonnées à l’origine différentes.
En algèbre, toutes les droites parallèles ont des équations similaires sauf la partie constante. Par exemple, les droites y = 2x + 1 et y = 2x – 3 sont parallèles.
insérer un filigrane dans Word
Lire la suite sur :
- Lignes parallèles
Lignes transversales
Les lignes transversales sont les lignes qui coupent deux ou plusieurs autres lignes.
Pour deux droites, les droites transversales forment 8 angles et dans le cas de droites parallèles, ces 8 angles présentent diverses propriétés et relations. Certains de ces angles sont des angles correspondants, des angles intérieurs alternés, des angles extérieurs alternés et des angles intérieurs consécutifs.
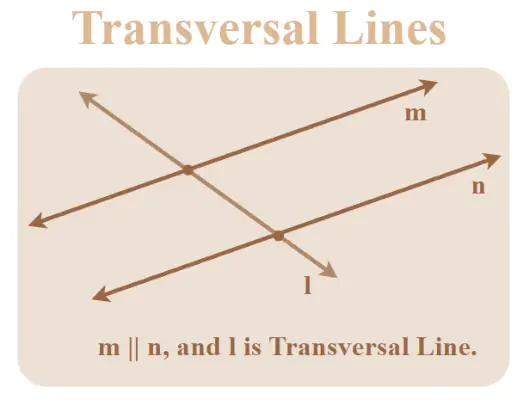
Illustration de la ligne transversale
Types spéciaux de lignes
Il existe différents types spéciaux de lignes en géométrie, à savoir :
- Lignes tangentes
- Lignes sécantes
- Lignes inclinées
- Lignes de symétrie
Discutons-en en détail.
Ligne tangente
Les lignes tangentes sont définies comme les lignes qui touchent la courbe ou l'objet géométrique en un seul point et ne se coupent plus jamais.
- Au point de contact, la tangente et la courbe ont la même pente, c'est-à-dire
dy/dx si y = f(x) est la courbe donnée.
- Dans le cas de deux dimensions, une tangente de n'importe quelle courbe en tout point représente le taux de changement instantané qui est le même que la pente.
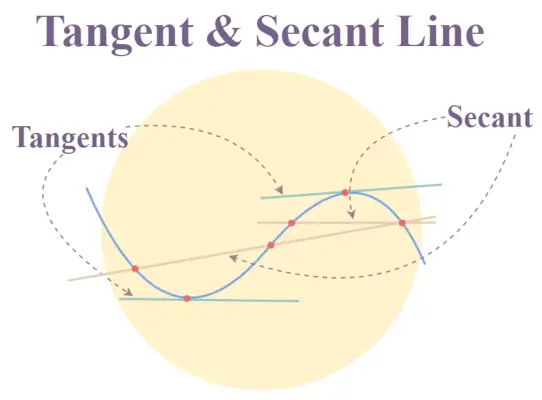
Illustration des lignes tangentes et sécantes
Ligne secante
D'un autre côté, les lignes sécantes sont différentes des tangentes car ces lignes coupent la courbe ou l'objet géométrique tel qu'un cercle en deux points distincts ou plus. Il existe certaines propriétés des lignes sécantes par rapport au cercle, appelées théorème sécant tangent et théorème sécant alternatif.
Ligne inclinée
Dans l’espace tridimensionnel, les lignes asymétriques sont ces paires de lignes qui ne se croisent ni ne sont parallèles les unes aux autres. Ils ne sont pas définis pour deux dimensions.

Axe de symétrie
Une ligne de symétrie est la ligne qui divise une forme en deux moitiés congruentes. Les deux moitiés sont l’image miroir l’une de l’autre. De ce fait, l’axe de symétrie est également appelé axe miroir.
Ce concept est appliqué à diverses formes géométriques, notamment les polygones, les lettres et les objets.

En savoir plus:
- Lignes et angles
- Types d'angles
- Points, lignes et plans
FAQ sur les types de lignes
Qu’est-ce que la Ligne ?
Une ligne est un chemin droit qui s’étend à l’infini dans les deux directions. Il n’a pas d’extrémité et est souvent représenté par une ligne droite avec des flèches aux deux extrémités. Une ligne peut être considérée comme un ensemble de points qui s’étendent indéfiniment dans les deux directions.
Définissez Ray.
Un rayon est une ligne droite qui s’étend à l’infini dans une direction à partir d’un point de départ spécifique appelé point final. Il n’a pas de point final défini dans l’autre sens et continue indéfiniment.
Définir un segment de ligne.
Un segment de droite est un chemin droit entre deux points dans l’espace. Il se compose des points finaux et de tous les points situés entre eux. Contrairement à une ligne, un segment de ligne a une longueur définie et peut être mesuré.
Quelle est la différence entre une ligne et un segment de ligne ?
Une ligne est infiniment longue sans extrémité, tandis qu'un segment de ligne a deux extrémités distinctes.
Combien de types de lignes existe-t-il en géométrie ?
Différents types de lignes, basés sur différents paramètres, sont :
- Lignes droites
- Lignes courbes
- Lignes en zigzag
- Lignes brisées ou lignes pointillées
- Lignes horizontales
- Lignes verticales
- Lignes diagonales
- Lignes d'intersection
- Lignes bissectrices
- Les lignes perpendiculaire
- Lignes parallèles
- Lignes transversales
Qu’est-ce que la ligne perpendiculaire ?
Une ligne perpendiculaire est une ligne qui forme un angle de 90 degrés avec une autre ligne ou surface. Si deux lignes se coupent et que les angles formés font tous 90 degrés, on dit qu’elles sont perpendiculaires l’une à l’autre.
Que sont les lignes parallèles ?
Les lignes parallèles sont des lignes qui se trouvent dans le même plan et ne se coupent jamais, quelle que soit leur extension. Ils ont la même pente et maintiendront toujours la même distance les uns des autres.
tutoriel de réaction js
Les lignes parallèles se rencontrent-elles ?
Non, les lignes parallèles ne se rencontrent jamais, même si nous étendons ces lignes à une distance infinie, elles ne se rencontrent jamais non plus.
Qu’est-ce que la ligne qui se croise ?
Une ligne sécante est une ligne qui croise ou rencontre une autre ligne en un point spécifique appelé point d'intersection. Lorsque deux lignes se croisent, elles partagent un point commun.
Qu’est-ce que la ligne transversale ?
Une ligne transversale est une ligne qui coupe deux ou plusieurs autres lignes en différents points. Il forme divers angles avec les lignes coupées, tels que des angles correspondants, des angles intérieurs alternés et des angles extérieurs alternés.
Qu’est-ce que la ligne inclinée ?
Les lignes obliques sont des lignes qui ne se trouvent pas dans le même plan et ne sont ni parallèles ni sécantes. Ce sont des lignes non coplanaires qui maintiennent une distance constante entre elles lorsqu’elles se déplacent dans l’espace.
Qu’est-ce que la ligne tangente ?
Une ligne tangente est une ligne qui touche une courbe ou une surface en un seul point et ne la coupe plus. Il représente la direction instantanée de la courbe en ce point.
Que sont les lignes concurrentes ?
Les lignes concurrentes sont trois lignes ou plus dans un plan qui se coupent en un seul point. Ce point d’intersection commun est appelé point de concurrence.
