Trapèze en mathématiques : Un trapèze est un polygone à quatre côtés, c'est-à-dire un quadrilatère. Trapèze vient du mot grec trapèze qui signifie table. C'est un quadrilatère complexe. Un trapèze est un quadrilatère spécial comportant une seule paire de côtés parallèles. Un trapèze est une forme bidimensionnelle qui ressemble à une table.
Un trapèze a quatre côtés et quatre sommets. Nous voyons la forme du trapèze dans notre vie quotidienne et c'est l'une des formes les plus courantes. Dans cet article, nous découvrirons qu'est-ce que le trapèze en mathématiques, ses propriétés, formules, exemples et types de trapèze, ainsi que quelques exemples résolus.
Table des matières
- Qu’est-ce qu’un trapèze en mathématiques ?
- Types de trapèze
- Trapèze irrégulier
- Propriétés du trapèze
- Formule trapèze
- Aire de formule du trapèze
- Périmètre de la formule du trapèze
- Différence entre trapèze et trapèze
- Angles du trapèze
- Diagonale du trapèze
- Exemples de trapèze
Qu’est-ce qu’un trapèze en mathématiques ?
Un trapèze est un quadrilatère bidimensionnel de forme fermée comportant une paire de côtés opposés parallèles. Les côtés parallèles d’un trapèze sont appelés bases et les côtés non parallèles d’un trapèze sont appelés jambes. Le trapèze a quatre côtés et quatre coins. UN parallélogramme est aussi appelé trapèze à deux côtés parallèles.
Définition du trapèze
Un trapèze est un quadrilatère (un polygone à quatre côtés) avec au moins une paire de côtés parallèles. Ces côtés parallèles sont appelés bases du trapèze, et les deux autres côtés sont appelés jambes, qui ne sont pas nécessairement parallèles.
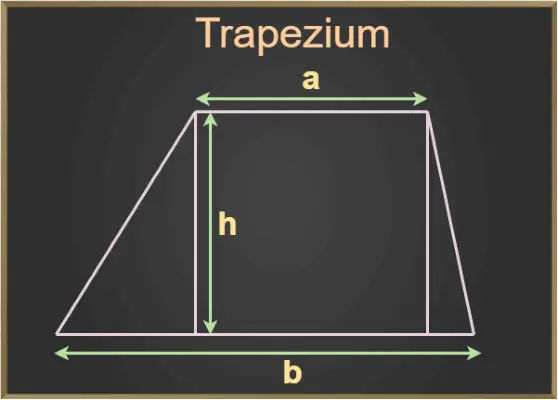
Dans la figure ci-dessus, a et b sont les bases du trapèze et h est la hauteur du trapèze.
Forme trapèze
Le trapèze est un quadrilatère c'est-à-dire un polygone à quatre côtés. Un trapèze a quatre côtés avec une paire de côtés opposés parallèles entre eux. La forme du trapèze est très courante et nous voyons diverses choses dans notre vie quotidienne qui ressemblent au trapèze. Certains exemples réels de trapèze que nous avons observés sont des tables, des carreaux, des peintures et autres en forme de trapèze.
héritage en Java
Types de trapèze
En fonction des côtés et des angles, le trapèze est de trois types :
- Trapèze scalène
- Trapèze isocèle
- Trapèze droit

Trapèze isocèle
Le trapèze qui a des branches de longueur égale est appelé trapèze isocèle, c'est-à-dire que dans un trapèze isocèle, les deux côtés non parallèles sont égaux.
Trapèze scalène
Un trapèze dont tous les côtés ne sont pas égaux est appelé trapèze scalène. Dans un trapèze scalène, il n’y a pas deux angles égaux.
Trapèze droit
Un trapèze comportant une paire d'angles droits adjacents l'un à l'autre est appelé trapèze droit.
Trapèze irrégulier
Un trapèze a une paire de côtés parallèles et les deux autres côtés ne sont pas parallèles. Dans un trapèze régulier, les deux autres côtés non parallèles sont égaux, mais dans le cas d'un trapèze irrégulier, les deux côtés opposés non parallèles sont inégaux.
Propriétés du trapèze
Il existe diverses propriétés du trapèze, dont certaines sont les suivantes :
- Côtés parallèles : Un trapèze a deux côtés parallèles, appelés bases. Exemple: Les côtés AB et CD sont parallèles entre eux, comme indiqué sur la figure.
- Côtés non parallèles : Les côtés non parallèles d’un trapèze sont appelés les jambes et les jambes d’un trapèze ne sont pas de même longueur. Exemple: Les côtés AD et BC sont des côtés non parallèles du trapèze.
- Hauteur ou altitude : La distance perpendiculaire entre les bases est appelée hauteur ou altitude du trapèze. Dans le diagramme ci-dessus, h est la hauteur du trapèze.
- Somme des angles
- Les angles intérieurs adjacents dans un trapèze totalisent 180°. Exemple: Il existe deux paires d'angles co-intérieurs. Une paire est ∠ A et ∠ D tandis que l'autre paire est ∠ B et ∠ C. La somme de chaque paire d'angles co-intérieurs est de 180°.
- La somme de tous les angles intérieurs d’un trapèze est toujours de 360°. Exemple : Sur la figure ∠A+∠D vaut 180° et ∠B+∠C vaut 180°. Donc ∠A+∠D +∠B+∠C = 360°.
- Médian: La médiane d'un trapèze est le segment de ligne qui relie les milieux des jambes. La médiane est parallèle aux bases et sa longueur est la moyenne des longueurs des bases.
- Le trapèze a exactement une paire de côtés opposés parallèles.
Formule trapèze
Les formules importantes d'un trapèze sont :
- Aire du trapèze = ½ (Somme des côtés parallèles) × (Distance entre les côtés parallèles)
- Périmètre du trapèze = Somme des quatre côtés
Aire de formule du trapèze
Le trapèze a respectivement deux côtés parallèles a et b, et sa hauteur est h.
L'aire du trapèze peut désormais être calculée en trouvant la moyenne des bases et en multipliant son résultat par l'altitude. Ainsi,
Aire du trapèze = ((une +b)/2) × h
où,
- un et b sont des bases de trapèze
- h est l'altitude
Aire du trapèze isocèle
Soit a et b la longueur des côtés parallèles d'un trapèze ABCD, où a et b sont les bases du trapèze et a>b.
Maintenant, comme il s’agit d’un trapèze isocèle, c est la longueur des deux côtés non parallèles et h est la hauteur du trapèze.
Maintenant, AB = a, CD = b, BC = AD = c
Dans Triangle rectangle , DEA
Longueur de la perpendiculaire, h = √(c 2 - (un B) 2 ) [en utilisant Théorème de Pythagore ]….(1)
Maintenant,
Aire = ½ × Somme des côtés parallèles × Hauteur du trapèze
Superficie = ½ × (a+b) × h
En utilisant l'équation (1)
Aire du trapèze isocèle = 1/2 × [√(c 2 - (un B) 2 ) (a+b)]
Périmètre de la formule du trapèze
Le périmètre d'un trapèze est donné en calculant la somme de tous ses côtés. Ainsi,
Périmètre du trapèze = AB + BC + CD + AD
où, AB, C.-B., CD et ANNONCE sont les côtés du trapèze
Périmètre du trapèze isocèle
Si dans un trapèze isocèle a et b sont les longueurs des côtés parallèles, c'est-à-dire les bases et c est la longueur de deux côtés égaux non parallèles, alors le périmètre est donné par :
Périmètre = a + b + 2c
où,
- un , b sont des bases de trapèze
- c est le côté égal du trapèze
Différence entre trapèze et trapèze
De manière générale, Trapezium et Trapezoid sont identiques, mais la différence réside dans leur pays d'origine.
- Trapèze est d'origine britannique, c'est un polygone à quatre côtés et une figure bidimensionnelle il a exactement une paire de côtés parallèles opposés l'un à l'autre. En Inde, nous suivons l'anglais britannique, c'est pourquoi le mot Trapezium est utilisé.
- Trapèze est d'origine américaine, c'est aussi un polygone à quatre côtés avec une paire de côtés parallèles opposés l'un à l'autre. Les côtés parallèles sont les bases et deux autres côtés non parallèles sont appelés les jambes du trapèze.
Angles du trapèze
Le trapèze est un quadrilatère et la somme de tous les angles d'un quadrilatère fait 360 degrés. La somme de tous les angles intérieurs du trapèze est donc de 360 degrés.
Pour tout trapèze régulier, c'est-à-dire le trapèze dans lequel les côtés non parallèles sont égaux aux angles adjacents formés entre la ligne parallèle et la ligne non parallèle est égal. Ainsi, la somme de ces deux angles est supplémentaire.
Prenons un exemple pour soutenir ce concept pour un trapèze isocèle ABCD si AB est parallèle à CD et AD est égal à CD alors, on sait que ∠A = ∠B et ∠C = ∠D alors,
∠A + ∠B + ∠C + ∠D = 360°
Ici, ∠A = ∠B et ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
De même, (∠B + ∠D) = 180°
Diagonale du trapèze
Le trapèze est un type particulier de quadrilatère ; ainsi, les trapèzes ont également deux diagonales. Les diagonales d'un trapèze n'ont pas des longueurs égales, contrairement à certains autres quadrilatères comme les rectangles ou les parallélogrammes. Les diagonales du trapèze n'ont pas des longueurs égales et les longueurs des diagonales dépendent des longueurs des bases et des angles du trapèze.
Exemple : Pour un trapèze isocèle ABCD, l'angle de base ∠A est de 80° puis trouvez l'autre angle ∠C.
On sait que pour un trapèze isocèle ABCD,
(∠A + ∠C) = 180°
Étant donné, ∠A = 80°
langage Java de baseMaintenant, 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
Ainsi, l'angle requis ∠C est de 100°
Formules de trapèze – Surface et périmètre du trapèze
Les formules liées au trapèze sont résumées dans le tableau suivant :
| Propriété | Formule |
|---|---|
| Zone | 1/2 × ( un + b ) × h |
| Aire (trapèze isocèle) | 1/2 × [√(c2- (un B)2) (a+b)] |
| Périmètre | un + b + c + d |
| Périmètre (trapèze isocèle) | un + b + 2 c |
| Médian | (un + b)/2 |
Les gens lisent également :
- Rhombe
- Triangle
- Quelle est la formule pour trouver l’aire du trapèze ?
Exemples de trapèze
Exemple 1 : Trouvez le quatrième côté du trapèze, si les trois autres côtés mesurent 8 cm, 12 cm et 16 cm et que le périmètre est de 40 cm.
Solution:
Le périmètre est donné comme la somme de tous ses côtés. Soit la longueur o inconnue égale à « x » unités.
Périmètre = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
La longueur du côté inconnu est donc de 4 cm.
Exemple 2 : Un trapèze a des côtés parallèles de 15 cm et 11 cm de longueur et des côtés non parallèles de 5 cm chacun. Calculer le périmètre de trapèze.
Solution:
C'est un Trapèze Isocèle car il est clairement mentionné que les côtés non parallèles de longueur 5 cm chacun sont égaux.
Selon le trapèze isocèle, si deux côtés non parallèles du trapèze sont de même longueur, il est alors connu sous le nom de trapèze isocèle.
Donné,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Périmètre = a + b + 2c
P = 15 + 11 + 2(5)
P = 15 + 11 + 10
P = 36 cm
Exemple 3 : Trouvez le périmètre d'un trapèze dont les côtés mesurent 12 cm, 14 cm, 16 cm et 18 cm.
Solution:
P = Somme de tous les côtés
P = 12 + 14 + 16 + 18
P = 60 cm
Le périmètre du trapèze est donc de 60 cm.
Exemple 4 : Trouvez l'aire du trapèze, dans laquelle la somme des côtés parallèles est de 60 cm et sa hauteur est de 10 cm.
Solution:
Donné,
- Somme des côtés parallèles 60 cm
- hauteur, h = 10 cm
Aire du trapèze, A = 1/2 × Somme des côtés parallèles × Distance entre les côtés parallèles
Substituer des valeurs données,
séléniumUNE =1/2×60×10
UNE = 30×10
A = 300 cm2
Par conséquent, l'aire du trapèze = 300 cm2
Problèmes de pratique sur le trapèze en mathématiques
1. Trouvez l’aire d’un trapèze dont les bases sont de 10 cm et 15 cm et dont la hauteur est de 6 cm.
2. Un trapèze a une superficie de 54 mètres carrés. Si l’une des bases mesure 12 mètres de long et 6 mètres de hauteur, trouvez la longueur de l’autre base.
3. Calculez le périmètre d'un trapèze dont les bases sont de 8 cm et 14 cm et les côtés non parallèles de 5 cm et 7 cm.
4. Déterminez la longueur du segment médian d'un trapèze dont les bases mesurent 18 cm et 30 cm.
5. Dans un trapèze isocèle, les angles à une base sont chacun de 45 degrés. Trouvez les mesures des angles à l’autre base. Supposons que le trapèze n’est pas un trapèze droit.
Résumé – Trapèze en mathématiques
Un trapèze est un polygone à quatre côtés, ou quadrilatère, caractérisé par une paire de côtés parallèles appelés bases, tandis que les deux autres côtés, appelés jambes, ne sont pas parallèles. Commun dans les objets du quotidien comme les tables, le trapèze se distingue par ses propriétés géométriques : il a une hauteur, qui est la distance perpendiculaire entre les bases, et une médiane qui relie les milieux des côtés non parallèles et est parallèle aux bases.
L'aire d'un trapèze est calculée en faisant la moyenne des longueurs des bases et en multipliant par la hauteur, tandis que son périmètre est la somme de tous ses côtés. Avec différentes classifications telles que les trapèzes scalènes, isocèles et droits, chacun avec des propriétés de côté et d'angle uniques, les trapèzes sont fondamentaux à la fois dans les applications pratiques et dans la théorie géométrique.
FAQ sur le trapèze en mathématiques
Qu'est-ce que la forme du trapèze ?
Le trapèze est un quadrilatère dans lequel deux droites sont toujours parallèles. Cela ressemble à la forme d’une table. Son nom est tiré du mot grec trapèze qui signifie table.
Combien de types de trapèze ?
Il existe deux types de trapèze,
- Trapèze régulier : Dans lequel l’autre paire de lignes est égale.
- Trapèze irrégulier : Dans lequel l’autre paire de lignes n’est pas égale.
Combien de côtés parallèles un trapèze a-t-il ?
Nous savons que le trapèze est un quadrilatère avec une paire de côtés parallèles. Ainsi, un trapèze a une paire de lignes (côtés) parallèles.
Un trapèze peut-il être considéré comme un quadrilatère ?
A a quatre côtés, quatre sommets et quatre angles. Il peut donc être considéré comme un quadrilatère, la somme des quatre angles intérieurs d'un trapèze est de 360 degrés.
Un carré peut-il être appelé trapèze ?
Un trapèze est un quadrilatère avec une seule paire de côtés parallèles et les deux autres côtés ne sont pas parallèles. Mais dans le cas d’un Carré, il possède deux paires de côtés parallèles et ne peut donc pas être considéré comme un Trapèze.
Les diagonales d'un trapèze sont-elles toujours égales ?
Les diagonales d'un trapèze peuvent ne pas être égales. Dans le cas d'un polygone régulier, les diagonales sont égales mais ce n'est pas vrai dans le cas d'un polygone irrégulier.
Quelles sont les propriétés d’un trapèze ?
Les 5 propriétés d’un Trapèze sont :
- Dans le trapèze, les bases sont parallèles entre elles.
- Un trapèze a des angles adjacents supplémentaires.
- Une seule paire de côtés opposés est parallèle.
- La somme de tous les angles intérieurs d’un trapèze est toujours de 360°.
- La ligne qui relie le milieu des côtés non parallèles est toujours parallèle aux bases.
