Le cercle unité est un cercle dont le rayon est 1. Le centre du cercle unité est à l'origine (0,0) sur l'axe. Le circonférence du cercle unitaire est de 2π unités, tandis que l'aire du cercle unitaire est de π unités2. Il porte toutes les propriétés de Circle. Le cercle unitaire a l'équation x2+ et2= 1. Ce cercle unitaire aide à définir divers concepts trigonométriques.
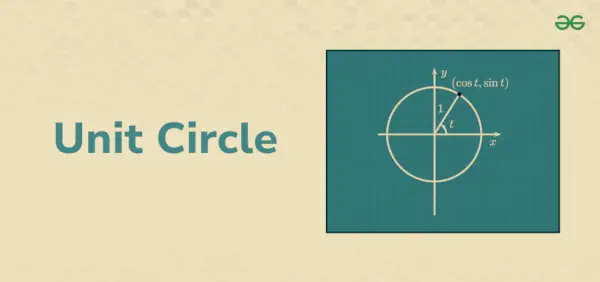
Cercle unité
Le cercle unitaire est souvent désigné par S1la généralisation à des dimensions supérieures est la sphère unitaire. Comprenons plus en détail ci-dessous les exemples de cercle unitaire, de formule et de résolution.
Qu’est-ce que le cercle unitaire ?
Le cercle unitaire est un cercle qui a un rayon de une (1) unité. Nous utilisons le plan cartésien pour tracer un cercle unité et un cercle unité est un polynôme de 2 degrés avec deux variables. Le cercle unité a diverses applications en trigonométrie et en algèbre et est principalement utilisé pour trouver les valeurs de différents rapports trigonométriques tels que sin x, cos x, tan x et autres.
Définition du cercle unitaire
En mathématiques, nous définissons un cercle unité comme le lieu d'un point fixe situé à une distance d'une unité du centre du cercle. Un cercle unitaire a un rayon d’une unité et donc le nom de cercle unitaire.
Équation du cercle unitaire
Nous savons que l’équation de tout cercle de centre (h, k) et de rayon « r » est :
(x-h) 2 + (o – k) 2 =r 2
Pour un cercle unitaire, nous savons que r est 1 unité et donc l'équation du cercle unitaire est,
(x-h) 2 + (o – k) 2 = 1
Formule du cercle unitaire
Si le centre du cercle unité est l'origine, c'est-à-dire (h, k) = (0, 0) alors l'équation du cercle unité est,
X 2 + et 2 = 1
Un cercle unité est représenté dans l'image ajoutée ci-dessous, avec la coordonnée centrale h, k et lorsque le cercle est à l'origine la valeur de h et k est nulle et le rayon AP est égal à 1 unité.
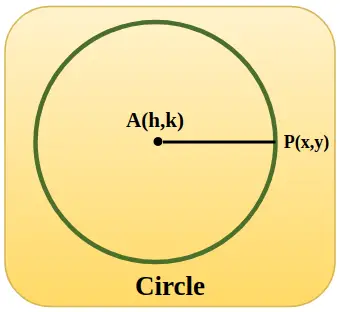
Fonctions trigonométriques utilisant le cercle unité
L'application du théorème de Pythagore dans un cercle unité peut être mieux utilisée pour comprendre les fonctions trigonométriques. Pour cela, nous considérons qu'un triangle rectangle est placé à l'intérieur d'un cercle unité dans le plan de coordonnées cartésien. Si l’on remarque, le rayon de ce cercle désigne l’hypoténuse du triangle rectangle.
Le rayon du cercle forme un vecteur. Cela conduit à la formation d’un angle, disons θ, avec l’axe des x positif. Supposons que x soit respectivement la longueur de base et y la longueur d'altitude du triangle rectangle. De plus, les coordonnées des extrémités du vecteur de rayon sont respectivement (x, y).
Le triangle rectangle contient respectivement les côtés 1, x et y. Le rapport trigonométrique peut maintenant être calculé comme suit :
sin θ = Altitude/Hypoténuse = y/1
cos θ = Base/Hypotenuse = x/1
Maintenant,
- péché θ = y
- cos θ = x
- tan θ = péché θ /cos θ = y/x
En substituant les valeurs de θ, on peut obtenir les valeurs principales de toutes les fonctions trigonométriques. De la même manière, des valeurs de fonctions trigonométriques à différentes valeurs sont trouvées.
Cercle unitaire avec Sin Cos et Tan
Tout point sur le cercle unité avec les coordonnées (x, y) est représenté en utilisant des identités trigonométriques comme (cosθ, sinθ). Les coordonnées des coins du rayon représentent le cosinus et le sinus des valeurs θ pour une valeur particulière de θ et la ligne de rayon. Nous avons cos θ = x et sin θ = y. Il y a quatre parties d'un cercle situées chacune dans un quadrant, formant un angle de 90°, 180°, 270° et 360°. Les valeurs de rayon se situent respectivement entre -1 et 1. De plus, les valeurs sin θ et cos θ se situent respectivement entre 1 et -1.
Cercle unitaire et identités trigonométriques
Les identités trigonométriques du cercle unitaire pour la cotangente, la sécante et la cosécante peuvent être calculées à l'aide des identités du péché, du cos et du bronzage. En conclusion, nous obtenons un triangle rectangle avec respectivement les côtés 1, x et y. Le calcul des identités du cercle unitaire peut être exprimé comme suit :
- péché θ = y/1
- cos θ = x/1
- bronzage θ = y/x
- sec θ = 1/x
- cosec θ = 1/y
- lit bébé θ = x/y
Graphique de cercle d'unité
Le diagramme circulaire unitaire est un diagramme qui contient la valeur de la fonction trigonométrique sinus et cosinus pour différents angles. Le diagramme de cercle unitaire pour celui-ci est ajouté ci-dessous,
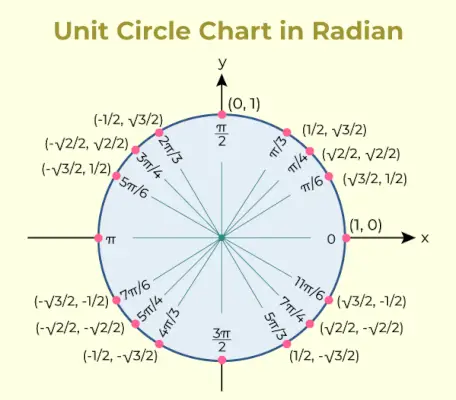
chaîne.valeur de java
Table de cercle d'unité
Les rapports trigonométriques utilisés dans le tableau du cercle unité sont utilisés pour répertorier les coordonnées des points sur le cercle unité qui correspondent à des angles communs.
| Angles | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sans | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| parce que | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| donc | 0 | 1/√(3) | 1 | √(3) | Non défini |
| csc | Non défini | 2 | √(2) | 23) | 1 |
| seconde | 1 | 23) | √(2) | 2 | Non défini |
| lit bébé ipconfig gratuit | Non défini | √(3) | 1 | 1/√(3) | 0 |
Identités pythagoriciennes du cercle unitaire
Il existe trois identités pythagoriciennes et toutes sont facilement prouvées en utilisant le concept de cercle unitaire que sont les trois identités pythagoriciennes,
- sans2θ + cos2θ = 1
- 1 + donc2θ = seconde2je
- 1 + lit bébé2θ = cosec2je
Plan complexe du cercle unitaire
Nombres complexes et le plan complexe s'expliquent facilement en utilisant le concept de cercle unité. L'équation du cercle unité sous forme complexe est,
|z| = 1
OU
X 2 + et 2 = 1
Sous la forme d’Euler, le nombre complexe est représenté par :
z = e il = cos t + je(péché t)
En savoir plus
Exemples résolus sur le cercle unitaire
Q1 : Montrer que le point Q se trouve sur un cercle unité, Q = [1/√(6), √4/√6]
Solution:
Donné,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
L'équation du cercle unitaire est,
X2+ et2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
gauche ≠ droite
Ainsi, le point Q[1/√(6), √4/√6] ne se trouve pas sur le cercle unité.
Q2 : Calculez donc 30 Ô en utilisant les valeurs sin et cos du cercle unité.
Solution:
caractère en chaîne java
tan 30° en utilisant les valeurs sin et cos,
tan 30° = (sin 30°)/ (cos 30°)
- sans 30° = 1/2
- cos 30° = √(3)/2
beige 30° = 1/2/√(3)/2
bronzage 30° = 1/√(3)
Q3 : Validez si le point P [1/2, √(3)/2] se situe sur le cercle unité.
Solution:
Donné,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
L'équation du cercle unitaire est,
- X2+ et2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= droite
Questions pratiques sur le cercle unitaire
T1. Vérifiez si les points A (1/2, 3/2) se trouvent sur un cercle unité.
Q2. Vérifiez si les points A (2, 1/2) se trouvent sur un cercle unité.
Q3. Trouver la valeur du cos 240°
Q4. Trouver la valeur du bronzage 320°
Q5. Trouver la valeur du sin 160°
Cercle unitaire – FAQ
Qu’est-ce que le cercle unitaire ?
Un cercle unité est défini comme l'emplacement d'un point situé à une unité d'un point fixe. Il a un centre en (0,0) et la valeur de son rayon est 1.
Comment vérifier si un point se trouve sur le cercle unitaire ?
Tout point situé dans un plan 2D de la forme (x, y) est mis dans l'équation du cercle unité x2+ et2= 1 pour vérifier s'il se trouve sur le cercle ou non.
Quelle est la formule du cercle unitaire ?
La formule du cercle unitaire est une formule utilisée pour représenter algébriquement un cercle unitaire. La formule du cercle unitaire est donnée par :
X 2 + et 2 = 1
Pourquoi s’appelle-t-on cercle unitaire ?
Un cercle unitaire est appelé cercle unitaire car il a un rayon de une (1) unité.
