Les lignes horizontales sont définies comme des lignes parallèles à l'horizon ou au sol, d'où le nom de ligne horizontale. . La ligne horizontale a une pente nulle, c'est-à-dire que l'angle d'inclinaison de ces lignes est de zéro degré. Si les lignes horizontales sont tracées sur les plans cartésiens, elles ne font qu'une intersection le long de l'axe y car elles sont toujours parallèles à l'axe x et ne le coupent jamais.
Dans cet article, nous découvrirons la ligne horizontale, ses propriétés, la pente de la ligne horizontale, l'équation de la ligne horizontale, des exemples et des FAQ liés aux lignes horizontales, et d'autres en détail.
booléen pour chaîner java
Table des matières
- Définition de la ligne horizontale
- Pente de la ligne horizontale
- Tracer une ligne horizontale
- Équation de ligne horizontale
- Test de ligne horizontale
- Lignes horizontales et verticales
- Différences entre les lignes verticales et les lignes horizontales
- Note courte sur la ligne horizontale
- Exemples de lignes horizontales
Définition de la ligne horizontale
Nous savons qu'une ligne est un chemin droit qui relie deux ou plusieurs points et s'étend jusqu'à l'infini. Ainsi, nous définissons les lignes horizontales comme des lignes parallèles au sol ou à l'horizon et situées à une hauteur constante du sol.
Si nous traçons ces lignes sur le système cartésien, alors ces lignes sont les lignes qui n'ont pas d'origine sur l'axe des x mais qui ont une origine sur l'axe des y. Les lignes horizontales ont une inclinaison nulle, c'est-à-dire qu'elles ont un angle nul avec l'axe des x ou avec le sol.
Les lignes horizontales constituent la base des différents objets, formes et figures que nous étudions en géométrie. Supposons que nous devions dessiner un rectangle , un carré , un triangle , trapèze , etc. alors la base de ces figures est principalement constituée de lignes horizontales. Nous observons également des mensonges horizontaux dans la vie réelle puisque les lignes sur le sol et le toit des pièces, la base des escaliers, etc. sont également constituées de lignes horizontales.
Ces lignes sont également appelées lignes de couchage car elles n'ont aucun mouvement vertical et restent toujours à une hauteur constante du sol. L'image ajoutée ci-dessous montre la ligne horizontale.
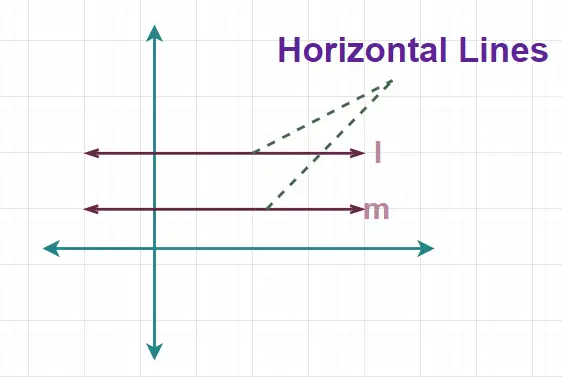
Ici, dans la figure ajoutée ci-dessus, les lignes l et m sont des lignes horizontales.
Pente de la ligne horizontale
Nous avons déjà mentionné que la pente de la ligne horizontale est nulle . Voyons maintenant comment la pente de la ligne horizontale est nulle. Nous calculons la pente d'une ligne horizontale en utilisant la formule,
Pente = Montée/Courir
OU
Pente de la ligne = Changement de coordonnée y/Changement de coordonnée x
Où Rise est la hauteur gagnée par la ligne en courant de gauche à droite, car nous savons déjà que la ligne horizontale est parallèle à l'axe des x et est toujours à la hauteur constante donc, nous disons que ces lignes ont une élévation nulle, donc la la pente de ces lignes est,
Ainsi, Pente = 0/Run = 0
On conclut donc que la pente de la ligne horizontale est nulle.
Tracer une ligne horizontale
Les lignes horizontales sont facilement tracées en suivant les étapes décrites ci-dessous,
Étape 1: Prenons un point du plan cartésien dont il faut trouver la ligne horizontale. Supposons que le point soit (1, 2)
Étape 2: Marque la coordonnée y du point. Dans ce cas, la coordonnée y est 2.
Étape 3: Marquez les autres points où la coordonnée y est la même que le point de l'étape 1. Laissez les autres points être (-2, 2), (0, 2) et (7, 2).
Étape 4: Joignez tous les points pour obtenir un segment de ligne et prolongez-les des deux côtés pour obtenir une ligne horizontale.
Il s'agit de la ligne horizontale requise passant par le point (1, 2) et ayant une pente nulle.

Équation de ligne horizontale
Nous savons que l'équation de la droite dans le système de coordonnées 2D est :
y = mx + c
Où,
- m est la pente de la droite
- c est l'ordonnée à l'origine sur l'axe y
On sait que pour la droite horizontale, la pente est nulle. En substituant cette valeur dans l'équation ci-dessus, nous obtenons l'équation de la ligne horizontale,
télécharger le lecteur multimédia YouTube VLC
y = 0x + c
y = c
Où c est une constante.
Ainsi, l’équation ci-dessus y = c est l’équation de la ligne horizontale.
Cette équation signifie que la ligne horizontale est une ligne qui passe par tous les points du cartésien où la coordonnée y est égale à « c ». Cette ligne coupée n'a pas de coordonnée x et donc cette ligne ne coupe jamais l'axe x et coupe l'axe y au point (0, c).
Ainsi, on peut dire que l'équation de la ligne horizontale est y = c (constante) et qu'elle passe par le point (a, c) où a peut prendre n'importe quelle valeur et c est toujours constant.
Test de ligne horizontale
Un test utilisé pour définir si une fonction est une fonction un-à-un ou non est le test de ligne horizontale. Dans le test de ligne horizontale, nous traçons une ligne horizontale passant par n'importe quel point de la fonction et si les lignes coupent la fonction en tout autre point, alors la fonction n'est PAS une fonction un-à-un. Ainsi, pour qu'une fonction soit biunivoque, elle doit réussir le test de la ligne horizontale, c'est-à-dire que toute ligne horizontale ne doit couper la fonction qu'une seule fois.
Nous savons que les fonctions un-à-un sont les fonctions pour lesquelles pour chaque valeur de x nous n'avons qu'une seule valeur de y. Ainsi, si la ligne horizontale traverse la fonction et ne la coupe qu’une seule fois alors on peut dire que pour la valeur unique de y, nous avons une valeur unique de x. Mais si la ligne horizontale coupe la fonction plus d’une fois alors nous obtenons deux valeurs pour la valeur unique de y, ce qui n’est pas le cas pour la fonction un-à-un.
Le test de ligne horizontale nous aide à déterminer si une fonction est une fonction One-One. Cela peut être compris à l’aide de l’image ajoutée ci-dessous.

Dans la première image, la fonction est biunivoque car la ligne horizontale ne passe que par un seul point de la fonction.
Dans la deuxième image, la fonction n'est PAS un à un car la ligne horizontale passe par plus d'un point de la fonction.
Lignes horizontales et verticales
Les lignes horizontales sont des lignes parallèles au sol ou à l'horizon. Ces lignes sont également appelées lignes de couchage. Dans le système cartésien, ces lignes sont parallèles à l'axe des x, tandis que pour les lignes verticales, ce sont les lignes perpendiculaires aux lignes horizontales, on les appelle les lignes debout. et sont parallèles à l'axe y dans le système cartésien.
Les lignes horizontales sont les lignes qui s'étendent de gauche à droite dans le système cartésien, tandis que les lignes verticales sont les lignes qui montent et descendent dans le système cartésien.
Les lignes verticales et horizontales sont perpendiculaires les unes aux autres. L'image ajoutée ci-dessous montre une ligne verticale et horizontale.

Différences entre les lignes verticales et les lignes horizontales
Les différences entre les lignes verticales et les lignes horizontales peuvent être facilement comprises en étudiant le tableau ajouté ci-dessous.
| Ligne horizontale | Ligne verticale |
|---|---|
| Ces lignes sont parallèles au sol ou à l'horizon. | Ces lignes sont perpendiculaire au sol ou à l'horizon. |
| La pente de la ligne horizontale est nulle. | La pente de la ligne verticale n'est pas définie. |
| La ligne horizontale fait un angle de zéro degré avec l'horizon. | La ligne verticale fait un angle de 90 degrés avec l'horizon. |
| L'équation de la ligne horizontale passant par le point (h, k) est : y = k | L'équation de la droite verticale passant par le point (h, k) est : x = h |
| Les lignes horizontales sont parallèles à l'axe des x dans le système cartésien. | Les lignes verticales sont parallèles à l'axe y dans le système cartésien. |
| Des exemples représentant les lignes horizontales sont,
| Des exemples représentant les lignes verticales sont :
|
Note courte sur la ligne horizontale
Une ligne horizontale en mathématiques est parfaitement plane, parallèle à l’horizon. Il s’étend de gauche à droite et a une pente de 0. En géométrie, il est représenté comme une ligne droite reliant deux points quelconques à la même hauteur sur un plan. L'équation pour une ligne horizontale est de la forme (y = k), où (k) est une valeur constante représentant la hauteur de la ligne sur l'axe y.
En savoir plus:
- Types de lignes
- Lignes parallèles
- Comment ajouter une ligne horizontale en HTML ?
- Comment utiliser l’espacement horizontal complet des lignes en HTML ?
- Comment dessiner des lignes horizontales et verticales dans une application Android à l'aide de XML
Exemples de lignes horizontales
Exemple 1 : Trouver l'équation de la droite horizontale passant par le point (1, -1).
Solution:
Nous savons que la pente de la ligne horizontale est m = 0.
Point donné (1, -1)
Équation de la droite passant par un point (x1, et1) et ayant une pente (m) est,
et et1= m(x – x1)
En remplaçant les valeurs dans l'équation ci-dessus, nous obtenons,
y – (-1) = 0(x – 1)
et + 1 = 0
y = -1
Ainsi, l’équation de la droite horizontale passant par le point (1, -1) est y = -1
Exemple 2 : Trouver l'équation de la droite horizontale passant par le point (5, 9).
Solution:
Nous savons que la pente de la ligne horizontale est m = 0.
commande d'exécution LinuxPoint donné (5, 9)
Équation de la droite passant par un point (x1, et1) et ayant une pente (m) est,
et et1= m(x – x1)
En remplaçant les valeurs dans l'équation ci-dessus, nous obtenons,
y – (9) = 0(x – 5)
et – 9 = 0
y = 9
Ainsi, l'équation de la ligne horizontale passant par le point (5, 9) est y = 9
Exemple 3 : Trouvez l'équation de la ligne horizontale lorsque l'ordonnée à l'origine de la ligne est 5.
Solution:
L'équation de la ligne horizontale est,
y = k
où k est l'ordonnée à l'origine
instanciation de JavaDonné
- k = 5
Équation de la ligne horizontale,
y = 5
Ainsi, la ligne horizontale de l’équation avec l’ordonnée à l’origine comme 5 est y = 5
Exemple 4 : Trouvez l'équation de la ligne horizontale lorsque l'ordonnée à l'origine de la ligne est -11/3.
Solution:
L'équation de la ligne horizontale est,
y = k
où k est l'ordonnée à l'origine
Donné
- k = -11/3
Équation de la ligne horizontale,
y = -11/3
3 ans = -11
3 ans + 11 = 0
Ainsi, la ligne horizontale de l’équation avec l’ordonnée à l’origine comme -11/3 est 3y + 11 = 0
Lignes horizontales – FAQ
Que sont les lignes horizontales ?
Les lignes horizontales sont des lignes parallèles à l'horizon ou au sol. Dans le système cartésien, les lignes horizontales sont parallèles à l’axe des x.
Quelle est l’équation de la ligne horizontale ?
L'équation de la ligne horizontale est,
y = k
où k est l'ordonnée à l'origine sur l'axe des y.
Quelle est la pente d’une ligne horizontale ?
La pente de la ligne horizontale est toujours égale à zéro, car elle fait un angle de zéro degré avec l'axe des x.
Quels sont des exemples de lignes horizontales ?
Des exemples représentant les lignes horizontales sont,
- Route droite
- Bas d'escalier
- Base de n'importe quelle figure, etc.
Comment s’appellent les lignes horizontales sur le globe ?
Les lignes horizontales qui courent sur le globe sont appelées latitudes et sont parallèles à l'équateur.
Quelles sont les propriétés des lignes horizontales ?
Diverses propriétés des lignes horizontales sont,
- Ils sont parallèles au sol, à l'horizon et à l'axe des x.
- Ils sont perpendiculaires à l'axe y.
- La pente de la ligne horizontale est nulle, etc.
Quelle ligne est verticale et horizontale ?
Une ligne verticale est parallèle à l'axe y et s'étend tout droit de haut en bas dans un plan de coordonnées, tandis qu'une ligne horizontale est parallèle à l'axe x et s'étend tout droit de gauche à droite.
Quelle est la pente d’une ligne horizontale et verticale ?
La pente d'une ligne indique son inclinaison et sa direction. Il est calculé comme le rapport entre le changement vertical et le changement horizontal entre deux points sur la ligne.
Que sont les lignes de points horizontales et verticales ?
Les lignes horizontales s'étendent de gauche à droite ou de droite à gauche et sont parallèles à l'axe des x, tandis que les lignes verticales s'étendent de haut en bas et sont parallèles à l'axe des y. Ces deux types de lignes sont perpendiculaires l’une à l’autre.
