Trois dimensions peuvent être mesurées : longueur, largeur et hauteur, pour tout objet que vous pouvez voir ou toucher. Il y a certaines dimensions de notre maison dans laquelle nous vivons. L’écran/moniteur rectangulaire que vous regardez a une largeur et une largeur égales à sa longueur. Pour chaque structure géométrique tridimensionnelle, la surface et le volume sont mesurés.
La zone couverte par la surface de l’objet est la superficie de tout objet donné. Alors que la quantité d'espace disponible dans un objet est le volume.
Table des matières
- Superficie
- Superficie totale
- Surface incurvée/Surface latérale
- Volume
- Exemples sur les superficies et les volumes
- FAQ sur les formules de surface et de volume
Superficie
La surface et le volume peuvent être calculés pour n’importe quelle forme géométrique tridimensionnelle (3D). La surface de toute zone est la région occupée par la surface d'un objet. Le volume est la quantité d'espace disponible dans un objet. Nous avons différents types de formes comme un hémisphère, une sphère, un cube, un cuboïde, un cylindre, etc. Toutes les formes tridimensionnelles ont une aire et un volume. Mais les formes bidimensionnelles comme les carrés, les rectangles, les triangles, les cercles, etc.
Ici en deux dimensions, on ne peut mesurer que la surface. La surface occupée par un objet tridimensionnel par sa surface extérieure est appelée surface. Il est mesuré en unités carrées.
La zone est de deux types :
- Superficie totale
- Surface incurvée/Surface latérale
Superficie totale
La surface comprenant la ou les bases et la partie incurvée correspond à la surface globale. C’est la superficie délimitée par la surface de l’objet. Si la forme a une base et une surface courbes, la somme des deux régions correspondra à la superficie totale. La Surface Totale peut être définie comme la surface totale couverte par un objet incluant sa base ainsi que la partie courbe. Si un objet possède à la fois une base et une zone courbe, la surface totale sera égale à la somme d'une base et d'une zone courbe.
- La surface totale est la surface totale occupée par un objet.
- Par exemple, prenons un cuboïde comme exemple : le cuboïde a 6 faces, 12 arêtes et 8 sommets.
Superficie totale = Superficie de base + Superficie courbe
mysql insérer dans
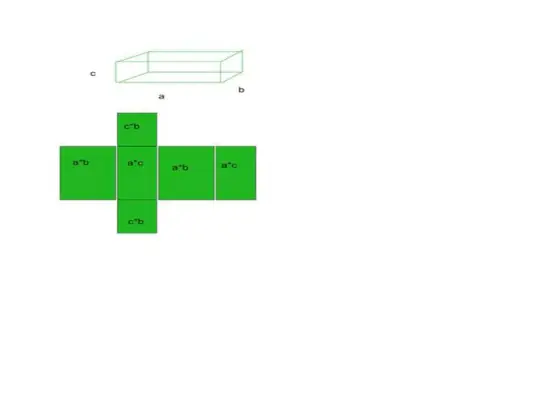
- La somme de toutes ces 6 zones sera notre surface totale de la forme particulière
Exemple:
Ci-dessous est un cuboïde dont les dimensions sont données comme longueur = 8 cm, largeur = 4 cm et hauteur = 6 cm, trouvez le TSA d'un cuboïde
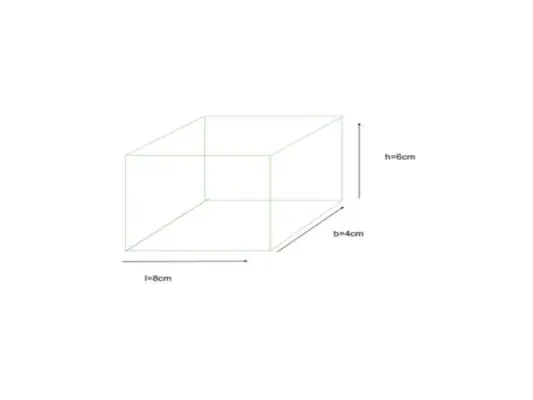
étant donné l = 8 cm, b = 4 cm, h = 6 cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
La TSA du cuboïde est de 208 cm.
Surface incurvée/Surface latérale
La surface courbe, à l'exception de son centre, correspond à la surface de la seule partie courbe de la ou des formes. Pour les formes telles qu’un cône, on l’appelle souvent surface latérale. La surface latérale peut être définie comme la zone qui comprend uniquement la surface incurvée d'un objet ou la surface latérale d'un objet en excluant la zone de base d'un objet. La surface latérale est également connue sous le nom de surface courbe.
La plupart des formes ou des objets font référence à la surface incurvée, la forme ou le cylindre en forme d'objet s'y réfère comme à une surface latérale. En simple, la zone qui nous est visible est appelée surface latérale. Par exemple, considérons le cylindre comme indiqué dans la figure ci-dessous.
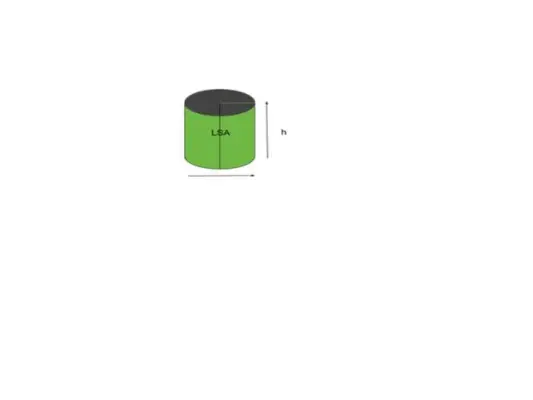
Volume
Le volume est la quantité d'espace dans un certain objet 3D. La quantité totale d'espace occupée par un objet ou une substance est appelée volume. Il est mesuré en unités cubes.
Formules de surface et de volume
Le tableau donné contient la surface totale, la surface incurvée/la surface latérale et le volume de diverses formes.
| Nom de la forme | Surface incurvée | Superficie totale | Volume |
|---|---|---|---|
| Cuboïde | 2h(déjeuner + petit déjeuner) | 2(lb + ch + hl) | l*b*h |
| cube | 4a2 | 6a2 | un3 |
| Cylindre | 2πrh | 2π(r + h) | πr2h |
| Sphère | 4πr2 chaîne n java | 4πr2 | 4/3πr3 |
| Cône | πrl | πr(r + l) | 1/3πr2h |
| Hémisphère | 2pr2 | 3πr2 | 2/3πr3 |
En savoir plus:
- Superficie de la pyramide
- Surface du cylindre
- Superficie de l'hémisphère
- Surface de la sphère
- Surface du cuboïde
Exemples sur les superficies et les volumes
Exemple 1 : 2 cubes chacun d'un volume de 512 cm 3 sont joints bout à bout. Trouver la surface du cuboïde résultant ?
Solution:
Donné,
Le volume (V) de chaque cube est = 512 cm3
nous pouvons maintenant impliquer qu'un3= 512 cm3
∴ Côté du cube, soit a = 8 cm
Désormais, la largeur et la longueur du cuboïde résultant seront de 8 cm chacune tandis que sa hauteur sera de 16 cm.
Donc, la surface du cuboïde (TSA) = 2(lb + bh + lh)
Maintenant, en mettant les valeurs, on obtient,
= 2(8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Donc TSA du cuboïde = 640 cm 2
Exemple 2 : Nous avons une bougie cylindrique de 14 cm de diamètre et de longueur 2 cm. On le fond pour former une bougie cuboïde de dimensions 7 cm × 11 cm × 1 cm. Combien de bougies cuboïdes peut-on obtenir ?
Solution:
Dimensions de la Bougie cylindrique :
Rayon de la bougie cylindrique = 14/2 cm = 7 cm
Hauteur/Epaisseur=2 cm
Volume d'une bougie cylindrique = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Volume du cuboïde bougie = 7 x 11 x 1 = 77 cm3
Par conséquent, nombre de bougies cuboïdes = Volume d'une bougie cuboïde/Volume d'une bougie cylindrique = 308/77 = 4
Nous pouvons donc obtenir 4 bougies de forme cuboïdale.
Exemple 3 : Une femme veut construire une boule de jouet sphérique en argile dont le rayon est égal au rayon du bracelet qu'elle porte. Étant donné que le bracelet est de forme circulaire, elle souhaite également que la surface du bracelet soit égale au volume de la sphère. Connaître le rayon du bracelet qu'elle porte ?
Solution:
Soit r le rayon du bracelet ainsi que la sphère,
On nous a dit que le volume de la sphère est égal à l’aire du bracelet :
Ainsi,
πr2= 4/3 πr3
⇒ r = 3/4
Le rayon du bracelet est donc de 3/4 unités.
Exemple 4 : On sait que la hauteur inclinée d'un cône circulaire droit est de 25 cm et sa hauteur est de 24 cm. Trouver la surface courbe du cône ?
Solution:
La formule de la surface courbe du cône est πrl. Où r est le rayon du cône et l est la hauteur inclinée du cône.
Ici, le cône est le cône circulaire droit.
Le rayon du cône serait donc :
r= sqrt{l^2 – h^2}
trier un tableau java=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Le calcul de la surface courbe est maintenant :
Surface requise = (22/7) * 7 * 25 = 550 cm2
La surface courbe du cône est donc de 550 cm. 2 .
Exemple 5 : Trouvez la surface latérale d'un cylindre avec un rayon de base de 6 pouces et une hauteur de 14 pouces.
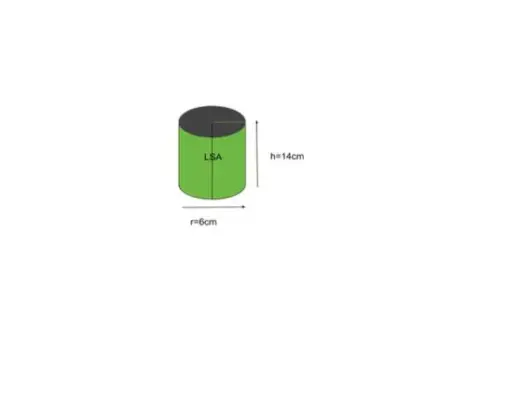
Solution:
Étant donné le rayon r = 6, la hauteur h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527 787
= 528.
Le LSA d'un cylindre donné est de 528 cm .
Question pratique sur les superficies et les volumes
Divers Questions pratiques sur les superficies et les volumes les formules sont :
T1. Trouvez l’aire d’un cube dont les côtés mesurent 5 centimètres.
Q2. Calculez le volume d'une sphère de rayon 3 mètres.
Q3. Déterminez la surface totale d'un cylindre de rayon 4 centimètres et de hauteur 8 centimètres.
Q4. Trouvez le volume d'un cône de rayon 6 pouces et de hauteur 10 pouces.
Q5. Calculez la surface d'un prisme rectangulaire de 7 mètres de longueur, 4 mètres de largeur et 6 mètres de hauteur.
FAQ sur les formules de surface et de volume
Quelles sont les formules de surface et de volume ?
Diverses formules de surface et de volume sont ajoutées dans l’article ci-dessus.
Quelle est la formule de la classe volumique de surface 10 ?
La formule pour la classe de surface et de volume 10 contient :
| Nom de la forme | Surface incurvée | Superficie totale | Volume |
|---|---|---|---|
| Cuboïde quelle est la taille de ce moniteur | 2h(déjeuner + petit déjeuner) | 2(lb + ch + hl) | l × b × h |
| cube | 4a2 | 6a2 | un3 |
| Cylindre | 2πrh | 2π(r + h) | πr2h |
| Sphère | 4πr2 | 4πr2 | 4/3πr3 |
| Cône | πrl | πr(r + l) | 1/3πr2h |
| Hémisphère | 2pr2 | 3πr2 | 2/3πr3 |
Quelle est la formule du Cuboïde en surface et en volume ?
- Surface du cuboïde = 2 (lb + bh + hl)
- Volume de Cubiod = l × b × h
Qu'est-ce que la surface et le volume ?
L'aire de surface est l'aire de toutes les surfaces d'un solide et son volume est l'espace occupé par le sloïde.
