Un cercle est composé de points situés à la même distance du centre du cercle. Une forme géométrique fermée est un cercle. Dans la vie de tous les jours, on voit des cercles en forme de roue, des pizzas, un fond rond, etc.

Parties d'un cercle

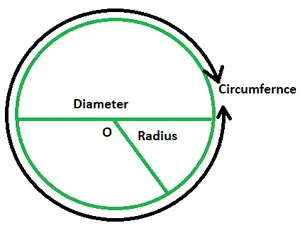
Mots clés:

• Rayon: Le rayon d'un cercle est la distance entre son centre et n’importe quel point du bord. Il est généralement noté r. Un cercle possède un nombre infini de rayons.
• Diamètre: C'est une ligne qui passe par le centre et a ses extrémités sur le cercle. Il est noté D et correspond au double de la valeur du rayon du cercle.
• Circonférence: L’étendue de la bordure du cercle est égale à sa circonférence. Cela signifie que le périmètre d’un cercle est égal à sa circonférence. La circonférence du cercle sera égale à la longueur du fil qui s'enroule parfaitement autour de son périmètre. Il est donné par 2πr.

Quelle est l’aire du cercle ?

L’aire d’un cercle se rapporte à la quantité d’espace entourée par le bord d’un cercle. La zone remplie par le cercle est le territoire situé dans le périmètre du cercle. On l’appelle également la quantité totale d’unités carrées incluses dans le cercle.

Vérifier: Diamètre d'un cercle

Formules d'aire de cercle

L’aire d’un cercle est donnée par la formule suivante :

A = πr ²

où r est le rayon du cercle donné.

ou

filtrage de Python

A = C ² /4p

où C est la circonférence du cercle donné.

Exemples utilisant la formule de l'aire du cercle

Question 1. Trouvez l'aire d'un cercle étant donné que son rayon est de 8 m.

Solution:

Étant donné : r = 8 m

Puisque l'aire d'un cercle = πr²

UNE = π(8)²

= 64p

= 200,96 m ²

'abc' est en chiffres'

Question 2. Trouvez l'aire d'un cercle étant donné que sa circonférence est de 12 cm.

Solution:

Étant donné : C = 12 cm

Puisque A = C²/4p

= 12²/4p

= 11,46 cm ²

Question 3. Trouvez l'aire d'un cercle étant donné que son diamètre est de 12 cm.

Solution:

Étant donné : D = 12 cm

jointure de chaîne Java

ou, Rayon = r = 12/2 = 6 cm

Puisque A = πr²

= π(6)2

= 113,04 cm ²

Question 4. Trouvez l'aire d'un cercle étant donné que son rayon est de 9 cm.

Solution:

Étant donné : r = 9 m

Puisque l'aire d'un cercle = πr²

connexions en Java

UNE = π(9)²

= 81p

= 254,34 cm ²

Question 5. Trouvez l'aire d'un cercle étant donné que son diamètre est de 10 cm.

Solution:

Étant donné : D = 10 cm

ou, Rayon = r = 10/2 = 5 cm

Puisque A = πr²

= π(5)²

= 78,5 cm ²

mvc-java

Vérifiez également :

• Calculateur d'aire d'un cercle
• Calculateur de superficie de cercle
• Calculateur de rayon d'un cercle
• Calculateur de diamètre d'un cercle
• Calculateur de circonférence
• Calculateur de circonférence en diamètre