La forme standard d'une parabole est y = hache²+ bx + c où a, b et c sont des nombres réels et a n'est pas égal à zéro. Une parabole est définie comme l'ensemble de tous les points d'un plan équidistants d'une ligne fixe et d'un point fixe du plan.

Dans cet article, nous comprendrons ce qu'est une parabole, l'équation standard d'une parabole, des exemples associés et d'autres en détail.

Table des matières

• Qu'est-ce qu'une parabole ?
• Équation d'une parabole
• Équations générales d'une parabole
• Équations standards d'une parabole
• Parties d'une parabole
• Exemples sur l'équation d'une parabole

Qu'est-ce qu'une parabole ?

Une parabole est une section conique définie comme l'ensemble de tous les points équidistants d'un point appelé foyer et d'une droite appelée directrice. Les équations standards pour une parabole dépendent de son orientation (sens d'ouverture) et de sa position.

Équation d'une parabole

L'équation de la parabole peut être écrite sous forme standard ou sous forme générale et les deux sont ajoutées ci-dessous :

Équations générales d'une parabole

L'équation générale d'une parabole est,

y = 4a(x – h) ² +k

(ou)

x = 4a(y – k) ² +h

Où (h, k) est le sommet d'une parabole.

Équations standards d'une parabole

L'équation standard d'une parabole est,

y = hache ² + bx + c

(ou)

x = est ² + par + c

où, a ne peut jamais être nul.

Parties d'une parabole

Certains termes et parties importants d’une parabole sont :

• Se concentrer: Le foyer est le point fixe d'une parabole.

• Directrice: La directrice d'une parabole est la droite perpendiculaire à l'axe d'une parabole.

• Accord Focal : La corde qui traverse le foyer d'une parabole, coupant la parabole en deux points distincts, est appelée corde focale.

• Distance focale : La distance focale est la distance d'un point (x₁, et₁) sur la parabole à partir du foyer.

• Côté droit: Un latus rectum est une corde focale qui passe par le foyer d'une parabole et est perpendiculaire à l'axe de la parabole. La longueur du grand rectum est LL’ = 4a.

• Excentricité: Le rapport entre la distance d'un point au foyer et sa distance à la directrice est appelé excentricité (e). Pour une parabole, l'excentricité est égale à 1, c'est-à-dire e = 1.

Une parabole possède quatre équations standards basées sur l'orientation de la parabole et son axe. Chaque parabole a un axe transversal et un axe conjugué différents.

Équation de la parabole	Parabole	Formules des paramètres d'une parabole
et 2 = 4ax	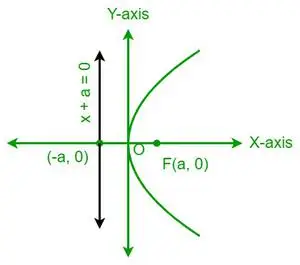Parabole horizontale	Sommet = (0,0) Foyer = (a, 0) La parabole s'ouvre sur le côté droit. L'équation de l'axe est y = 0 L'équation de la directrice est x + a = 0 Longueur du grand rectum = 4a
et 2 = -4ax	Parabole horizontale	Sommet = (0,0) Focus = (-a, 0) La parabole s'ouvre sur le côté gauche. L'équation de l'axe est y = 0 L'équation de la directrice est x – a = 0 Longueur du grand rectum = 4a
X 2 = 4 jours	Parabole verticale	Sommet = (0,0) Foyer = (0, a) La parabole s'ouvre vers le haut. L'équation de l'axe est x = 0 L'équation de la directrice est y + a = 0 Longueur du grand rectum = 4a
X 2 = -4ay	Parabole verticale	Sommet = (0,0) Foyer = (0, -a) La parabole s'ouvre vers le bas. L'équation de l'axe est x = 0 L'équation de la directrice est y – a = 0 Longueur du grand rectum = 4a

Voici les observations faites à partir de la forme standard des équations d’une parabole :

• Une parabole est symétrique par rapport à son axe. Par exemple, y²= 4ax est symétrique par rapport à l'axe des x, alors que x²= 4ay est symétrique par rapport à l'axe y.

• Si une parabole est symétrique par rapport à l'axe des x, alors la parabole s'ouvre vers la droite si le coefficient x est positif et vers la gauche si le coefficient x est négatif.

• Si une parabole est symétrique par rapport à l'axe y, alors la parabole s'ouvre vers le haut si le coefficient y est positif et vers le bas si le coefficient y est négatif.

Voici les équations standard d'une parabole lorsque l'axe de symétrie est parallèle à l'axe des x ou à l'axe des y et que le sommet n'est pas à l'origine.

Équation de la parabole	Parabole	Formules des paramètres d'une parabole
(et K)2= 4a(x – h)	Parabole horizontale	Sommet = (h, k) Focalisation = (h + a, k) La parabole s'ouvre sur le côté droit. L'équation de l'axe est y = k L'équation de la directrice est x = h – a Longueur du grand rectum = 4a
(et K)2= -4a(x – h)	Parabole horizontale	Sommet = (h, k) Foyer = (h – a, k) La parabole s'ouvre sur le côté gauche. L'équation de l'axe est y = k L'équation de la directrice est x = h + a Longueur du grand rectum = 4a
(x-h)2= 4a(y – k)	Parabole verticale	Sommet = (h, k) Foyer = (h, k + a) La parabole s'ouvre vers le haut. L'équation de l'axe est x = h L'équation de la directrice est y = k – a Longueur du grand rectum = 4a
(x-h)2= -4a(y – k)	Parabole verticale	Sommet = (h, k) Foyer = (h, k – a) La parabole s'ouvre vers le bas. L'équation de l'axe est x = h L'équation de la directrice est y = k + a Longueur du grand rectum = 4a

Équation de dérivation de la parabole

Soit P un point de la parabole dont les coordonnées sont (x, y). D'après la définition d'une parabole, la distance du point P au foyer (F) est égale à la distance de ce même point P à la directrice d'une parabole. Considérons maintenant un point X de la directrice dont les coordonnées sont (-a, y).

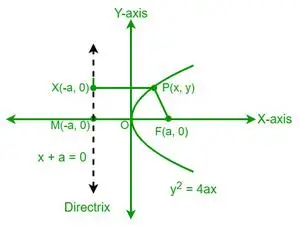
De la définition de l’excentricité d’une parabole, on a

e = FP/PX = 1

⇒ PF = PX

Les coordonnées du foyer sont (a, 0). Maintenant, en utilisant la formule de distance de coordonnées, nous pouvons trouver la distance du point P (x, y) au foyer F (a, 0).

PF = √[(x – une)²+ (et – 0)²]

⇒ PF = √[(x – a)²+ et²] ------ (1)

L'équation de la directrice est x + a = 0. Pour trouver la distance de PX, nous utilisons la formule de la distance perpendiculaire.

PX = (x + a)/√[1²+0²]

⇒ PX = x +a —————— (2)

Nous savons déjà que PF = PX. Donc, assimilez les équations (1) et (2).

√[(x – une)²+ et²] = (x + une)

En nous mettant au carré des deux côtés, nous obtenons,

⇒ [(x – une)²+ et²] = (x + une)²

⇒x²+ un²– 2ax + y²=x²+ un²+ 2ax

⇒ et²– 2ax = 2ax

⇒ et²= 2ax + 2ax ⇒ et ² = 4ax

Ainsi, nous avons dérivé l’équation d’une parabole. De même, nous pouvons dériver les équations standards des trois autres paraboles.

• et²= -4ax
• X²= 4 jours
• X²= -4ay

et ² = 4ax, et ² = -4ax,x ² = 4ay, et x ² = -4ay sont les équations standards d’une parabole.

Articles liés à la parabole :

• Équation du cercle
• Équation d'ellipse
• Équation de l'hyperbole
• Applications de la parabole dans la vie réelle

Exemples sur l'équation d'une parabole

Exemple 1 : Trouvez la longueur du latus rectum, du foyer et du sommet, si l'équation de la parabole est y ² = 12x.

Solution:

Donné,

L'équation de la parabole est y²= 12x

En comparant l'équation donnée avec la forme standard y²= 4ax

4a = 12

⇒ une = 12/4 = 3

Nous savons que,

Côté droit d'une parabole = 4a = 4 (3) = 12

Maintenant, foyer de la parabole = (a, 0) = (3, 0)

Sommet de la parabole donnée = (0, 0)

Exemple 2 : Trouvez l'équation de la parabole qui est symétrique par rapport à l'axe X et passe par le point (-4, 5).

Solution:

Donné,

La parabole est symétrique par rapport à l'axe X et a son sommet à l'origine.

Ainsi, l’équation peut être de la forme y²= 4ax ou y²= -4ax, où le signe dépend si la parabole s'ouvre vers la gauche ou vers la droite.

La parabole doit s'ouvrir à gauche puisqu'elle passe par (-4, 5) qui se situe dans le deuxième quadrant.

L’équation sera donc : y²= -4ax

En remplaçant (-4, 5) dans l'équation ci-dessus,

⇒ (5)²= -4a(-4)

⇒ 25 = 16a

⇒ une = 25/16

L’équation de la parabole est donc : y²= -4(25/16)x (ou) 4y²= -25x.

Exemple 3 : Trouver les coordonnées du foyer, de l'axe, de l'équation de la directrice et du grand rectum de la parabole x ² = 16 ans.

Solution:

Donné,

L'équation de la parabole est : x²= 16 ans

En comparant l'équation donnée avec la forme standard x²= 4 jours,

4a = 16 ⇒ a = 4

Le coefficient de y est positif donc la parabole s'ouvre vers le haut.

De plus, l’axe de symétrie est le long de l’axe Y positif.

Ainsi,

Le foyer de la parabole est (a, 0) = (4, 0).

L'équation de la directrice est y = -a, c'est-à-dire y = -4 ou y + 4 = 0.

Longueur du grand rectum = 4a = 4(4) = 16.

Exemple 4 : Trouvez la longueur du latus rectum, du foyer et du sommet si l'équation d'une parabole est 2(x-2) ² + 16 = oui.

Solution:

Donné,

L'équation d'une parabole est 2(x-2)²+ 16 = et

En comparant l'équation donnée avec l'équation générale d'une parabole y = a(x – h)²+ k, on obtient

une = 2

(h, k) = (2, 16)

Nous savons que,

Longueur du grand rectum d'une parabole = 4a

= 4(2) = 8

Maintenant, focus = (a, 0) = (2, 0)

Maintenant, Sommet = (2, 16)

Exemple 5 : L'équation d'une parabole est x ² – 12x + 4y – 24 = 0, puis trouvez son sommet, son foyer et sa directrice.

Solution:

Donné,

L'équation de la parabole est x²– 12x + 4 ans – 24 = 0

⇒x²– 12x + 36 – 36 + 4 ans – 24 = 0

⇒ (x – 6)²+ 4 ans – 60 = 0

⇒ (x – 6)²= -4(y + 15)

L'équation obtenue est sous la forme (x – h)²= -4a(y – k)

-4a = -4 ⇒ a = 1

Donc, le sommet = (h, k) = (6, – 15)

Foyer = (h, k – a) = (6, -15-1) = (6, -16)

L'équation de la directrice est y = k + a

⇒ y = -15 + 1 ⇒ y = -14

⇒ y + 14 = 0

FAQ sur l'équation de la parabole

Comment trouver l’équation standard d’une parabole ?

La forme standard de la parabole est y²= 4ax ou x²= 4 jours.

Quelle est l’équation normale de la parabole ?

Équation de la normale à la parabole y²= 4ax avec une pente m est donné par : y = mx – 2h – matin ³

Comment trouver le sommet d'une parabole ?

Pour une parabole donnée : y = ax²+ bx + c son sommet peut être trouvé en utilisant la formule x = − b/2a. Rebranchez cette valeur x dans l'équation pour trouver la coordonnée y correspondante.

entité relationnelle