Dans cet article, nous discuterons du parcours post-ordre dans la structure de données.
Les structures de données linéaires telles que la pile, le tableau, la file d'attente, etc. n'ont qu'un seul moyen de parcourir les données. Mais dans une structure de données hiérarchique telle que arbre , il existe plusieurs façons de parcourir les données. Nous allons donc discuter ici d'une autre façon de parcourir la structure de données arborescente, c'est-à-dire parcours de vente par correspondance . Le parcours post-ordre est l'une des techniques de parcours utilisées pour visiter le nœud dans l'arborescence. Il suit le principe LRN (nœud gauche-droite) . Le parcours post-ordre est utilisé pour obtenir l’expression suffixe d’un arbre.
Les étapes suivantes sont utilisées pour effectuer le parcours post-commande :
- Parcourez le sous-arbre de gauche en appelant la fonction postorder de manière récursive.
- Parcourez le sous-arbre de droite en appelant la fonction postorder de manière récursive.
- Accédez à la partie données du nœud actuel.
La technique de parcours post-ordre suit le Racine gauche droite politique. Ici, Left Right Root signifie que le sous-arbre gauche du nœud racine est traversé en premier, puis le sous-arbre droit et enfin, le nœud racine est traversé. Ici, le nom Postorder lui-même suggère que le nœud racine de l'arbre serait enfin traversé.
Algorithme
Voyons maintenant l'algorithme de parcours post-ordre.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: POSTORDER(TREE -> LEFT) Step 3: POSTORDER(TREE -> RIGHT) Step 4: Write TREE -> DATA [END OF LOOP] Step 5: END
Exemple de parcours de vente par correspondance
Voyons maintenant un exemple de parcours post-commande. Il sera plus facile de comprendre le processus de parcours post-commande à l'aide d'un exemple.
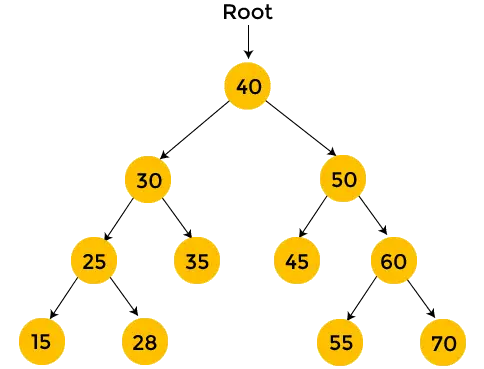
Les nœuds de couleur jaune ne sont pas encore visités. Maintenant, nous allons parcourir les nœuds de l'arborescence ci-dessus en utilisant le parcours post-ordre.
- Ici, 40 est le nœud racine. Nous visitons d'abord le sous-arbre gauche de 40, c'est-à-dire 30. Le nœud 30 traversera également en ordre post. 25 est le sous-arbre gauche de 30, il est donc également parcouru dans l'ordre post. Alors 15 est le sous-arbre gauche de 25. Mais 15 n’a pas de sous-arbre, donc imprimer 15 et déplacez-vous vers le sous-arbre droit de 25.
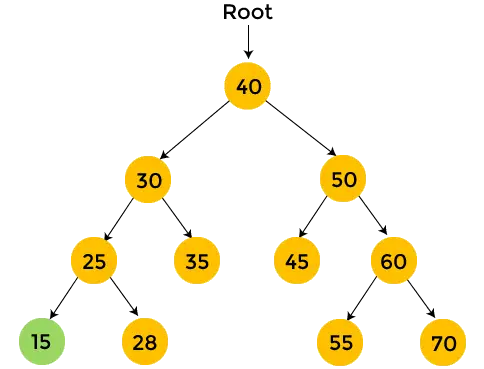
- 28 est le sous-arbre droit de 25 et il n'a pas d'enfants. Donc, imprimer 28 .
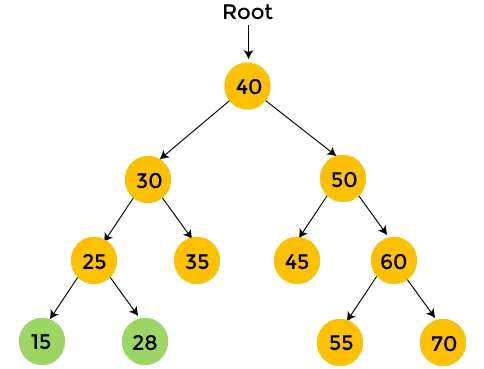
- Maintenant, imprimer 25 , et le parcours post-ordre pour 25 est fini.
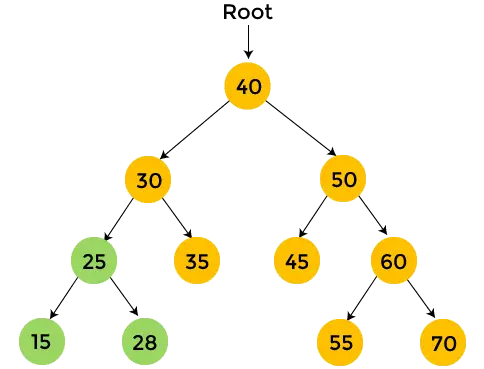
- Ensuite, déplacez-vous vers le sous-arbre droit de 30. 35 est le sous-arbre droit de 30 et il n’a pas d’enfants. Donc, imprimer 35 .
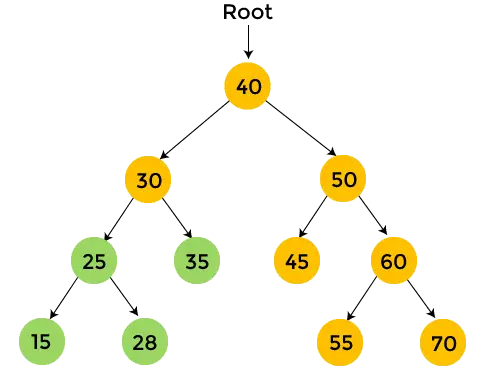
- Après cela, imprimer 30 , et le parcours post-ordre pour 30 est fini. Ainsi, le sous-arbre gauche de l'arbre binaire donné est parcouru.
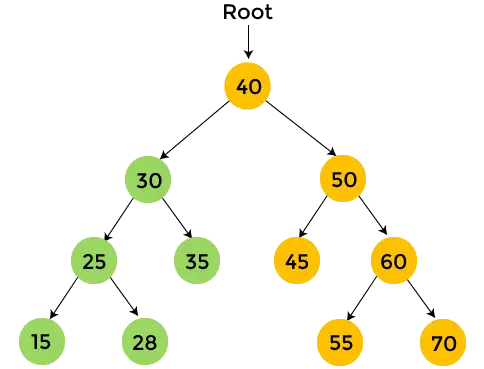
- Maintenant, déplacez-vous vers le sous-arbre droit de 40 qui est 50, et il traversera également dans l'ordre post. 45 est le sous-arbre gauche de 50 et il n’a pas d’enfants. Donc, imprimer 45 et déplacez-vous vers le sous-arbre droit de 50.
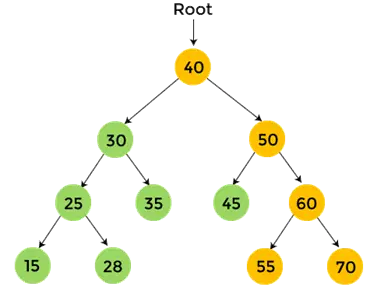
- 60 est le sous-arbre droit de 50, qui sera également parcouru en post-ordre. 55 est le sous-arbre gauche de 60 qui n'a pas d'enfants. Donc, imprimer 55 .
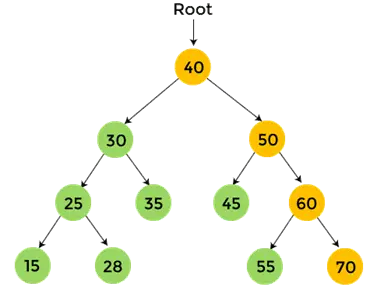
- Maintenant, imprimer 70, qui est le sous-arbre droit de 60.
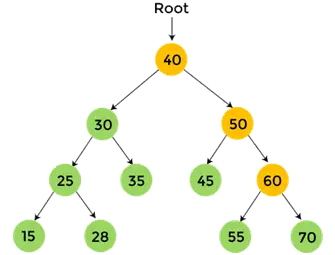
- Maintenant, imprimer 60, et le parcours post-ordre pour 60 est terminé.
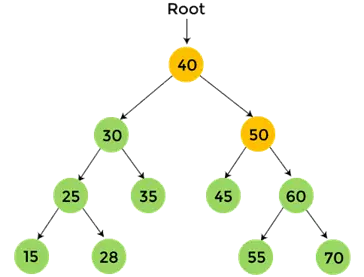
- Maintenant, imprimer 50, et le parcours post-ordre pour 50 est terminé.
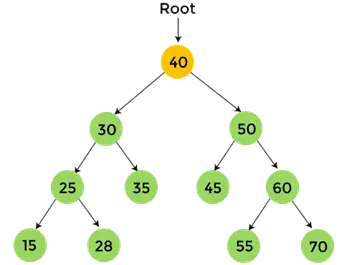
- Enfin, imprimer 40, qui est le nœud racine de l'arbre binaire donné, et le parcours post-ordre pour le nœud 40 est terminé.
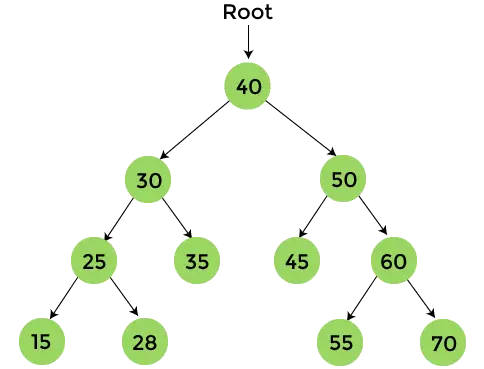
Le résultat final que nous obtiendrons après le parcours post-ordre est -
{15, 28, 25, 35, 30, 45, 55, 70, 60, 50, 40}
Complexité du parcours de vente par correspondance
La complexité temporelle du parcours post-ordre est Sur) , où 'n' est la taille de l'arbre binaire.
Alors que la complexité spatiale du parcours post-ordre est O(1) , si l'on ne considère pas la taille de la pile pour les appels de fonction. Sinon, la complexité spatiale du parcours post-ordre est Oh) , où « h » est la hauteur de l'arbre.
Implémentation du parcours de vente par correspondance
Voyons maintenant l'implémentation du parcours post-ordre dans différents langages de programmation.
Programme: Écrivez un programme pour implémenter le parcours post-ordre en langage C.
#include #include struct node { s struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Sortir

Programme: Écrivez un programme pour implémenter le parcours post-ordre en C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the postorder traversal of given binary tree is -
'; traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-14.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-15.webp" alt="Postorder Traversal"> <p> <strong>Program:</strong> Write a program to implement postorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/85/postorder-traversal-16.webp" alt="Postorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Sortir
Après l'exécution du code ci-dessus, le résultat sera -

Programme: Écrivez un programme pour implémenter le parcours post-ordre en Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PostorderTraversal { Node root; PostorderTraversal() { root = null; } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { PostorderTraversal pt = new PostorderTraversal(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } Sortir
Après l'exécution du code ci-dessus, le résultat sera -

Donc, c'est tout à propos de l'article. J'espère que l'article vous sera utile et informatif.











