QU'EST-CE QU'UNE PENTE ?

Un certain nombre de valeurs absolues indiquant si une ligne est plus raide ou plus plat et le direction de la ligne sur le graphique sont appelés pente ou pente. La pente d'une droite est un concept fondamental en économie et en mathématiques. Il est généralement désigné par la lettre 'je'. La pente peut être calculée en divisant le 'changement vertical' avec le 'changement horizontal' entre deux points distincts sur une ligne.

TYPES DE PENTE

Il existe deux principaux types de pistes répertoriées ci-dessous :

Pente positive :Pente dans laquelle deux variables, c'est-à-dire la variable sur l'axe des x et la variable sur l'axe des y, montrent une relation positive est connu comme pente positive. En termes plus simples, une pente positive est une pente dans laquelle la variable x augmente avec l'augmentation de la variable y et/ou la variable y augmente avec l'augmentation de la variable x. De même, la variable x diminue avec la diminution de la variable y, et/ou la variable y diminue avec la diminution de la variable x. Cela signifie que les deux variables sont compléments les uns aux autres. Une pente positive se déplace dans le direction ascendante ou est pente ascendante.
En termes graphiques, une pente positive est une pente dans laquelle la ligne du graphique monte lorsqu'elle se déplace de gauche à droite. Le concept de pente positive peut être clairement compris à l'aide du courbe d'offre d'un producteur ou d'une entreprise en économie. Les deux variables de la courbe sont le prix sur l’axe des y et la quantité de biens sur l’axe des x. Supposons que l'entreprise produise les biens pour maximisation des profits. Par conséquent, lorsque les prix des biens augmentent, la quantité fournie par l’entreprise de ces biens augmentera également, tandis que lorsque les prix diminuent, la quantité fournie par l’entreprise diminuera. En d’autres termes, à des prix plus élevés, l’entreprise ou le producteur augmentera la quantité fournie pour réaliser plus de profit, tandis qu’à des prix plus bas, il réduira la quantité fournie pour réduire la perte. Par conséquent, cela montre que les prix et la quantité fournie sont positivement liés les uns aux autres, ce qui peut être clairement démontré dans le diagramme ci-dessous :
Pente négative :Pente dans laquelle deux variables, c'est-à-dire la variable sur l'axe des x et la variable sur l'axe des y, montrent une relation négative est connu comme pente négative. En d’autres termes, une pente négative est une pente dans laquelle la variable x augmente avec la diminution de la variable y et/ou la variable y augmente avec la diminution de la variable x. De la même manière, la variable x diminue avec l'augmentation de la variable y, et/ou la variable y diminue avec l'augmentation de la variable x. Cela représente un relation inverse entre ces deux variables. Une pente négative se déplace dans le direction vers le bas ou est inclinée vers le bas.
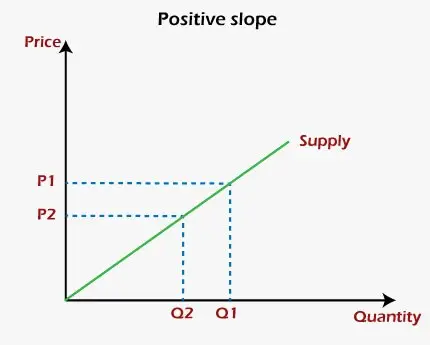
Graphiquement, une pente négative est une pente dans laquelle la ligne du graphique tombe lorsqu'elle se déplace de gauche à droite. L'un des meilleurs exemples de pente négative du graphique est le courbe de la demande en économie. Les deux variables de la courbe sont le prix sur l’axe des y et la quantité de biens sur l’axe des x. Comme nous le savons, les consommateurs achètent une grande quantité d’un bien à un prix inférieur plutôt qu’à un prix plus élevé. Par conséquent, la quantité demandée par les consommateurs de biens diminuera avec l’augmentation des prix de ces biens. D’un autre côté, lorsque les prix des biens diminuent, la demande quantitative augmente. Par conséquent, cela montre un relation négative entre les prix et la quantité fournie de ces biens. Cela peut être dégagé du schéma ci-dessous :

DEUX AUTRES TYPES DE PENTE

Outre les pentes positives et négatives, il existe deux autres types de pentes appelées pente nulle et pente infinie. Ils peuvent être compris à partir de l’explication donnée :

Pente nulle :Une condition dans laquelle la variable sur l'axe des y reste la même avec le changement de la variable sur l'axe des x est connue sous le nom de pente de zéro. Graphiquement, un ligne horizontale ou plate sur le graphique a une pente nulle. C'est pourquoi on l'appelle un fonction constante. Une pente de zéro ne se déplace ni vers le haut ni vers le bas. Il se déplace uniquement vers la gauche ou vers la droite.
Le diagramme ci-dessous est une présentation graphique de la pente nulle :
Pente infinie :Une condition dans laquelle la variable sur l'axe des x reste la même avec le changement de la variable sur l'axe des y est connue sous le nom de pente infinie. On l'appelle aussi le pente indéfinie. Selon les termes graphiques, un ligne verticale ou perpendiculaire sur le graphique a une pente infinie. Une pente infinie ne se déplace ni vers la gauche ni vers la droite. Il montre un mouvement uniquement vers le haut ou vers le bas.
Une pente infinie est représentée dans le diagramme donné :

CALCUL DE LA PENTE

• Dans une équation linéaire de hache + par + c = 0, la pente est définie comme -un B.
• L'équation de la droite peut être calculée à l'aide de la formule point-pente si la pente m d'une ligne et d'un point (x1, y1) sont connus. La formule est donnée ci-dessous :
  y - y1 = m (x - x1)
• Les deux lignes seront parallèle si leurs pentes sont égal, tandis que deux lignes seront perpendiculaire si le produit de leurs pentes est -1.

INFORMATIONS COMPLÉMENTAIRES

• La valeur absolue de la pente permet de déterminer si une courbe est plus raide ou plus plat.
• La valeur positive et négative de la pente décide de la direction, c'est-à-dire vers le haut ou vers le bas, de la pente.
• Une courbe devient plus raide avec l'augmentation de la valeur absolue de la pente.
• Une courbe devient flatté avec la diminution de la valeur absolue de la pente.
• Ces conditions ne sont pas affectées par le pente négative ou positive (pas la valeur négative ou positive).
• UN pente positive inférieure implique qu’une courbe plus plate inclinée vers le haut sera formée.
• UN pente positive plus élevée signifie qu’une courbe plus raide courbée vers le haut sera formée.
• UN pente négative avec une grande valeur absolue implique qu’une courbe plus raide inclinée vers le bas sera formée.
• UN pente négative ayant une valeur absolue plus petite signifie qu’une courbe plus plate courbée vers le bas sera formée.