Inférieur à égal à est un concept d'inégalité qui signifie que le terme du côté gauche de l'inégalité ne doit pas être supérieur au terme du côté droit, c'est-à-dire que le terme de gauche doit être inférieur ou au maximum égal au terme de droite. L'article couvre le concept de inférieur ou égal à en mathématiques, en introduisant le symbole ≤ et sa représentation sur une droite numérique. Il comprend un tableau de symboles mathématiques, des problèmes pratiques et des réponses aux questions fréquemment posées sur les inégalités.
Table des matières
réalisateur Karan Johar
- Inférieur à égal au signe
- Symbole inférieur ou égal à
- Inférieur ou égal à sur une droite numérique
- Notations symboliques des inégalités
- Inférieur à égal à et supérieur à égal à
Inférieur à égal au signe
Le signe inférieur à égal est ajouté dans l'image ci-dessous,
Qu'est-ce qui est inférieur ou égal à ?
Inférieur ou égal à signifie qu’une chose n’est pas plus qu’une autre ou peut être la même. Par exemple, si nous avons 2x – 3 ≤ 9, cela signifie que 2 fois un nombre (x) moins 3 n’est pas supérieur à 9. En simplifiant, si on ajoute 3 des deux côtés, on obtient 2x ≤ 12. Ensuite, en divisant des deux côtés par 2, nous trouvons x ≤ 6. Cela signifie donc que le nombre (x) peut être 6 ou moins, et c'est toujours vrai.
Vérifiez également
- Moins que le symbole
- Signe égal
Inférieur à égal à l'exemple
Disons que John et Peter sont deux amis et que l'âge de John est inférieur ou égal à celui de Peter. Cela signifie que Jean est soit plus jeune, soit égal à l'âge de Pierre. En d’autres termes, nous pouvons dire que Pierre est soit plus âgé, soit au minimum égal à l’âge de Jean.
Maintenant, disons que l’âge de Jean est de x ans et que celui de Pierre est de « y » ans, alors sous la forme de l’équation impliquant Inférieur à Égal à, nous pouvons écrire ceci comme suit :
x ≤ y
où,
- x est l'âge de John
- y est l'âge de Peter
Symbole inférieur ou égal à
Symbole inférieur ou égal à. est ≤
Il est utilisé en mathématiques pour comparer deux quantités. Plus précisément, lorsque vous voyez a ≤ b, cela signifie que a est inférieur ou égal à b. Ce symbole combine l'idée de inférieur à (<) et égal à (=). Ainsi, cela indique que la valeur sur le côté gauche du symbole est soit inférieure, soit identique à la valeur sur le côté droit. Cela permet d'exprimer des relations entre des nombres ou des expressions mathématiques où l'un peut être inférieur ou égal à l'autre.
Inférieur ou égal à sur une droite numérique
Le concept de inférieur ou égal à sur une droite numérique est une expression mathématique fondamentale utilisée pour comparer des valeurs numériques. Dans ce contexte, cela signifie qu'un nombre donné est soit inférieur, soit égal à un autre nombre. Lors de la représentation de cette relation sur une droite numérique, un cercle fermé (•) est placé sur le point correspondant à la valeur la plus petite ou égale. Par exemple, x ≤ 2 est représenté comme suit sur la droite numérique
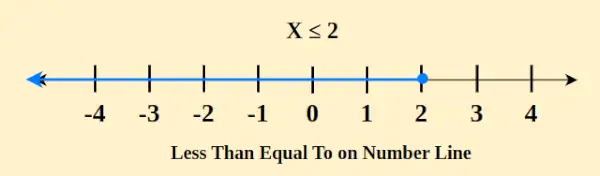
De plus, une ligne s'étend vers la droite à partir de ce point, englobant tous les nombres supérieurs ou égaux à la valeur désignée. L'inclusion d'un cercle fermé sert à souligner que le point final fait partie de la comparaison. Pour illustrer, si A ≤ B, le point A peut être positionné au niveau ou à gauche du point B sur la droite numérique, indiquant que A est inférieur ou égal à B, avec inclusion vers la possibilité que A soit égal à B. Cette représentation visuelle aide à comprendre les ampleurs relatives des valeurs comparées.
Notations symboliques des inégalités
Les différents signes d’inégalités utilisés ainsi que leur description sont ajoutés ci-dessous :
| Notation des symboles d’inégalités | |
|---|---|
| Symbole Description | Notation des symboles |
| Plus grand que le signe | > |
| Moins que le signe | < |
| Égal à signer | = |
| Pas égal au signe | ≠ |
| Supérieur inférieur ou égal à | ≥ |
| Inférieur ou égal à | ≤ |
Inférieur à égal à et supérieur à égal à
La comparaison entre supérieur à égal à et inférieur à égal à mentionnée ci-dessous :
| Différence entre supérieur à égal à et inférieur à égal à | ||
|---|---|---|
| Aspect | Supérieur à égal à | Inférieur à égal à |
| Signification | Indique la valeur qui est supérieure ou minimale égale à la valeur donnée | Indiquer la valeur qui est inférieure ou au maximum égale à la valeur donnée |
| Symbole | ≥ | ≤ |
| Exemple | L'âge du bélier est supérieur à 10 ans ⇒ Âge du Bélier ≥ 10 | L'âge de Rohan est inférieur à 15 ans ⇒ Âge du Rohan ≤ 15 |
Lectures connexes ,
- Supérieur à Inférieur à
- Plus grand ou égal à
- Inégalités
Inférieur à égal à – Exemples
Exemple 1. Résolvez l'inégalité : 3x – 5 ≤ 10.
Solution:
Commencez par ajouter 5 des deux côtés :
Ridhima Tiwari3x ≤ 15
Ensuite, divisez par 3 : x ≤ 5
Donc la solution est x ≤ 5
Exemple 2. Résolvez l'inégalité : -2y + 7 ≤ 1.
Solution:
Soustraire 7 des deux côtés : -2y ≤ -6
Divisez par -2 en n'oubliant pas d'inverser le signe de l'inégalité : y ≥ 3
La solution est y ≥ 3
Inférieur à égal à – Problèmes de pratique
Essayez les problèmes pratiques suivants basés sur le concept de inférieur à égal à
T1. Résolvez l’inégalité : 2y – 8 est inférieur ou égal à 10.
Q2. Si m vaut 6 et n vaut 3, déterminez si m au carré moins 5 est inférieur ou égal à 2n plus 1.
Q3. Résolvez x : 3x plus 7 est inférieur ou égal à 22.
Q4. Si q est un nombre positif tel que 4q moins 6 est inférieur ou égal à 14, trouvez les valeurs possibles pour q.
Q5. Déterminez la plage de valeurs de a qui satisfont à l’inégalité 2a plus 5 est inférieure ou égale à 15.
Inférieur à égal à – FAQ
1. À quoi est inférieur ou égal ?
Inférieur ou égal à désigne une relation entre deux valeurs, ce qui implique que la première valeur est soit inférieure, soit égale à la seconde.
2. Comment Inférieur à ou Égal à est-il représenté sur une droite numérique ?
Sur une droite numérique, cette relation est représentée visuellement en plaçant un cercle fermé (•) sur le nombre correspondant à la valeur inférieure ou égale et en prolongeant une ligne vers la droite, englobant tous les nombres supérieurs ou égaux à cette valeur.
3. Que signifie le cercle fermé sur la droite numérique ?
Le cercle fermé met l’accent sur l’inclusion du point final dans la comparaison. Si, par exemple, A ≤ B, cela indique que le point A est au niveau ou à gauche du point B sur la droite numérique, y compris la possibilité que A soit égal à B.
4. Quel est un exemple de résolution d’une inégalité inférieure ou égale à ?
Considérons l'inégalité 2x – 3 ≤ 9. Si nous ajoutons 3 aux deux côtés, nous obtenons 2x ≤ 12. Ensuite, en divisant les deux côtés par 2, nous trouvons x ≤ 6. Par conséquent, la solution de l'inégalité est x ≤ 6.
5. Comment résoudre les inégalités inférieures ou égales à ?
Pour résoudre des inégalités telles que ax + b ≤ c, l'approche habituelle consiste à manipuler l'inégalité par addition, soustraction, multiplication ou division pour isoler la variable et déterminer la plage de valeurs qui satisfont l'inégalité.
6. Quel est le symbole de inférieur à égal à et supérieur à égal à ?
Le symbole inférieur à égal à est ≤ tandis que le symbole supérieur à égal à est ≥.
