UN table de hachage est une structure de données qui permet une insertion, une suppression et une récupération rapides de données. Cela fonctionne en utilisant une fonction de hachage pour mapper une clé à un index dans un tableau. Dans cet article, nous allons implémenter une table de hachage en Python en utilisant un chaînage séparé pour gérer les collisions.
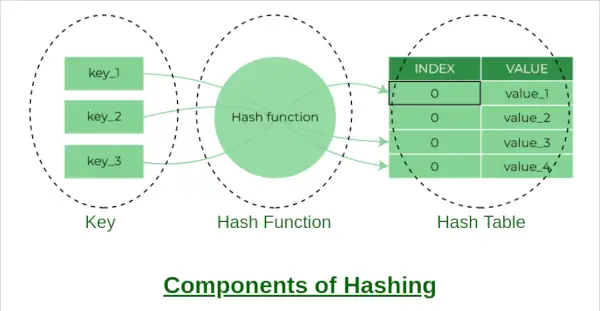
Composants du hachage
Le chaînage séparé est une technique utilisée pour gérer les collisions dans une table de hachage. Lorsque deux clés ou plus correspondent au même index dans le tableau, nous les stockons dans une liste chaînée à cet index. Cela nous permet de stocker plusieurs valeurs dans le même index tout en pouvant les récupérer à l'aide de leur clé.
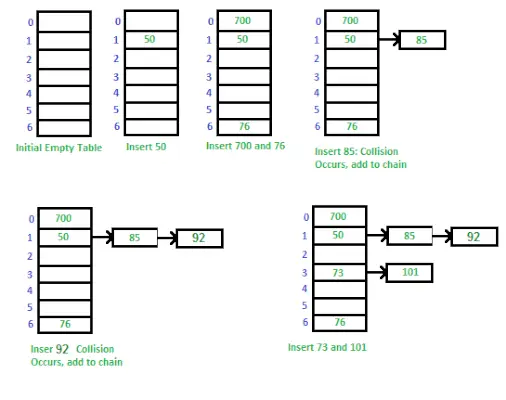
Façon d'implémenter une table de hachage en utilisant un chaînage séparé
Méthode d'implémentation d'une table de hachage à l'aide d'un chaînage séparé :
Créez deux classes : ' Nœud ' et ' Table de hachage '.
Le ' Nœud La classe ‘ représentera un nœud dans une liste chaînée. Chaque nœud contiendra une paire clé-valeur, ainsi qu'un pointeur vers le nœud suivant de la liste.
Python3
class> Node:> >def> __init__(>self>, key, value):> >self>.key>=> key> >self>.value>=> value> >self>.>next> => None> |
>
Kat Timf
>
La classe « HashTable » contiendra le tableau qui contiendra les listes chaînées, ainsi que des méthodes pour insérer, récupérer et supprimer des données de la table de hachage.
Python3
class> HashTable:> >def> __init__(>self>, capacity):> >self>.capacity>=> capacity> >self>.size>=> 0> >self>.table>=> [>None>]>*> capacity> |
>
>
algorithme k-nn
Le ' __chaud__ ‘ La méthode initialise la table de hachage avec une capacité donnée. Il définit le ' capacité ' et ' taille ' variables et initialise le tableau à 'Aucun'.
La méthode suivante est la ' _hacher ' méthode. Cette méthode prend une clé et renvoie un index dans le tableau où la paire clé-valeur doit être stockée. Nous utiliserons la fonction de hachage intégrée de Python pour hacher la clé, puis utiliserons l'opérateur modulo pour obtenir un index dans le tableau.
Python3
def> _hash(>self>, key):> >return> hash>(key)>%> self>.capacity> |
>
>
Le 'insérer' La méthode insérera une paire clé-valeur dans la table de hachage. Il prend l'index où la paire doit être stockée en utilisant le ' _hacher ' méthode. S'il n'y a pas de liste chaînée à cet index, il crée un nouveau nœud avec la paire clé-valeur et le définit comme tête de liste. S'il existe une liste chaînée à cet index, parcourez la liste jusqu'à ce que le dernier nœud soit trouvé ou que la clé existe déjà, et mettez à jour la valeur si la clé existe déjà. S'il trouve la clé, il met à jour la valeur. S'il ne trouve pas la clé, il crée un nouveau nœud et l'ajoute en tête de liste.
Python3
def> insert(>self>, key, value):> >index>=> self>._hash(key)> >if> self>.table[index]>is> None>:> >self>.table[index]>=> Node(key, value)> >self>.size>+>=> 1> >else>:> >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >current.value>=> value> >return> >current>=> current.>next> >new_node>=> Node(key, value)> >new_node.>next> => self>.table[index]> >self>.table[index]>=> new_node> >self>.size>+>=> 1> |
>
>
Le recherche La méthode récupère la valeur associée à une clé donnée. Il obtient d'abord l'index où la paire clé-valeur doit être stockée à l'aide du _hacher méthode. Il recherche ensuite la clé dans la liste chaînée à cet index. S'il trouve la clé, il renvoie la valeur associée. S'il ne trouve pas la clé, il génère un Erreur de clé .
trier une liste de tableaux
Python3
def> search(>self>, key):> >index>=> self>._hash(key)> >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >return> current.value> >current>=> current.>next> >raise> KeyError(key)> |
>
>
Le 'retirer' La méthode supprime une paire clé-valeur de la table de hachage. Il obtient d'abord l'index où la paire doit être stockée en utilisant le ` _hacher `méthode. Il recherche ensuite la clé dans la liste chaînée à cet index. S'il trouve la clé, il supprime le nœud de la liste. S'il ne trouve pas la clé, il génère un ` Erreur de clé `.
Python3
def> remove(>self>, key):> >index>=> self>._hash(key)> > >previous>=> None> >current>=> self>.table[index]> > >while> current:> >if> current.key>=>=> key:> >if> previous:> >previous.>next> => current.>next> >else>:> >self>.table[index]>=> current.>next> >self>.size>->=> 1> >return> >previous>=> current> >current>=> current.>next> > >raise> KeyError(key)> |
découpage de tableau Java
>
>
'__str__' méthode qui renvoie une représentation sous forme de chaîne de la table de hachage.
Python3
def> __str__(>self>):> >elements>=> []> >for> i>in> range>(>self>.capacity):> >current>=> self>.table[i]> >while> current:> >elements.append((current.key, current.value))> >current>=> current.>next> >return> str>(elements)> |
>
>
Voici l'implémentation complète de la classe 'HashTable' :
Python3
class> Node:> >def> __init__(>self>, key, value):> >self>.key>=> key> >self>.value>=> value> >self>.>next> => None> > > class> HashTable:> >def> __init__(>self>, capacity):> >self>.capacity>=> capacity> >self>.size>=> 0> >self>.table>=> [>None>]>*> capacity> > >def> _hash(>self>, key):> >return> hash>(key)>%> self>.capacity> > >def> insert(>self>, key, value):> >index>=> self>._hash(key)> > >if> self>.table[index]>is> None>:> >self>.table[index]>=> Node(key, value)> >self>.size>+>=> 1> >else>:> >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >current.value>=> value> >return> >current>=> current.>next> >new_node>=> Node(key, value)> >new_node.>next> => self>.table[index]> >self>.table[index]>=> new_node> >self>.size>+>=> 1> > >def> search(>self>, key):> >index>=> self>._hash(key)> > >current>=> self>.table[index]> >while> current:> >if> current.key>=>=> key:> >return> current.value> >current>=> current.>next> > >raise> KeyError(key)> > >def> remove(>self>, key):> >index>=> self>._hash(key)> > >previous>=> None> >current>=> self>.table[index]> > >while> current:> >if> current.key>=>=> key:> >if> previous:> >previous.>next> => current.>next> >else>:> >self>.table[index]>=> current.>next> >self>.size>->=> 1> >return> >previous>=> current> >current>=> current.>next> > >raise> KeyError(key)> > >def> __len__(>self>):> >return> self>.size> > >def> __contains__(>self>, key):> >try>:> >self>.search(key)> >return> True> >except> KeyError:> >return> False> > > # Driver code> if> __name__>=>=> '__main__'>:> > ># Create a hash table with> ># a capacity of 5> >ht>=> HashTable(>5>)> > ># Add some key-value pairs> ># to the hash table> >ht.insert(>'apple'>,>3>)> >ht.insert(>'banana'>,>2>)> >ht.insert(>'cherry'>,>5>)> > ># Check if the hash table> ># contains a key> >print>(>'apple'> in> ht)># True> >print>(>'durian'> in> ht)># False> > ># Get the value for a key> >print>(ht.search(>'banana'>))># 2> > ># Update the value for a key> >ht.insert(>'banana'>,>4>)> >print>(ht.search(>'banana'>))># 4> > >ht.remove(>'apple'>)> ># Check the size of the hash table> >print>(>len>(ht))># 3> |
instruction java if else
>
>Sortir
True False 2 4 3>
Complexité temporelle et complexité spatiale :
- Le complexité temporelle de la insérer , recherche et retirer Les méthodes dans une table de hachage utilisant un chaînage séparé dépendent de la taille de la table de hachage, du nombre de paires clé-valeur dans la table de hachage et de la longueur de la liste chaînée à chaque index.
- En supposant une bonne fonction de hachage et une distribution uniforme des clés, la complexité temporelle attendue de ces méthodes est O(1) pour chaque opération. Cependant, dans le pire des cas, la complexité temporelle peut être Sur) , où n est le nombre de paires clé-valeur dans la table de hachage.
- Cependant, il est important de choisir une bonne fonction de hachage et une taille appropriée pour la table de hachage afin de minimiser le risque de collision et garantir de bonnes performances.
- Le complexité de l'espace d'une table de hachage utilisant un chaînage séparé dépend de la taille de la table de hachage et du nombre de paires clé-valeur stockées dans la table de hachage.
- La table de hachage elle-même prend O(m) espace, où m est la capacité de la table de hachage. Chaque nœud de liste chaînée prend O(1) espace, et il peut y avoir au plus n nœuds dans les listes chaînées, où n est le nombre de paires clé-valeur stockées dans la table de hachage.
- La complexité totale de l’espace est donc O(m+n) .
Conclusion:
En pratique, il est important de choisir une capacité appropriée pour la table de hachage afin d'équilibrer l'utilisation de l'espace et la probabilité de collisions. Si la capacité est trop petite, la probabilité de collisions augmente, ce qui peut entraîner une dégradation des performances. En revanche, si la capacité est trop grande, la table de hachage peut consommer plus de mémoire que nécessaire.
