Dans un premier temps, nous comprendrons le arbre binaire et arbre de recherche binaire séparément, puis nous examinerons les différences entre un arbre binaire et un arbre de recherche binaire.

Qu'est-ce qu'un arbre binaire ?

UN Arbre binaire est unPointeur vers l'enfant de gauche :Il stocke la référence du nœud enfant gauche.Pointeur vers le bon enfant :Il stocke la référence du nœud enfant droit.Élément de données :L'élément de données est la valeur des données stockées par le nœud.

L'arbre binaire peut être représenté comme suit :

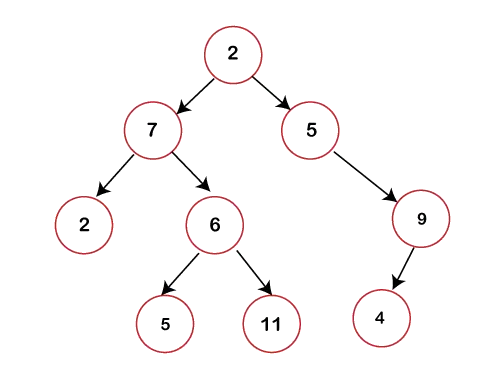
Dans la figure ci-dessus, nous pouvons observer que chaque nœud contient au maximum 2 enfants. Si un nœud ne contient pas d'enfant gauche ou droit, la valeur du pointeur par rapport à cet enfant serait NULL.

Les terminologies de base utilisées dans un arbre binaire sont :

Noeud principal:Le nœud racine est le premier ou le nœud le plus élevé d’un arbre binaire.Nœud parent :Lorsqu'un nœud est connecté à un autre nœud via des bords, ce nœud est alors appelé nœud parent. Dans un arbre binaire, le nœud parent peut avoir au maximum 2 enfants.Nœud enfant :Si un nœud a son prédécesseur, alors ce nœud est appelé un nœud enfant .Noeud feuille:Le nœud qui ne contient aucun enfant appelé noeud feuille .Nœud interne :Le nœud qui a au moins 2 enfants appelé nœud interne .Profondeur d'un nœud :La distance entre le nœud racine et le nœud donné est appelée profondeur d'un nœud . Nous fournissons des étiquettes à tous les nœuds, comme le nœud racine est étiqueté avec 0 car il n'a pas de profondeur, les enfants des nœuds racine sont étiquetés avec 1, les enfants de l'enfant racine sont étiquetés avec 2.Hauteur:La distance la plus longue entre le nœud racine et le nœud feuille est la hauteur du nœud .

Dans un arbre binaire, il existe un arbre appelé arbre binaire parfait . C'est un arbre dans lequel tous les nœuds internes doivent contenir deux nœuds, et tous les nœuds feuilles doivent être à la même profondeur. Dans le cas d'un arbre binaire parfait, le nombre total de nœuds existants dans un arbre binaire peut être calculé à l'aide de l'équation suivante :

n = 2^m+1-1

qui a fait l'école

où n est le nombre de nœuds, m est la profondeur d'un nœud.

Qu’est-ce qu’un arbre de recherche binaire ?

UN Arbre de recherche binaire est un arbre qui suit un certain ordre pour organiser les éléments, alors que l'arbre binaire ne suit aucun ordre. Dans un arbre de recherche binaire, la valeur du nœud gauche doit être inférieure à celle du nœud parent et la valeur du nœud droit doit être supérieure à celle du nœud parent.

Comprenons le concept d'arbre de recherche binaire à travers des exemples.

Dans la figure ci-dessus, nous pouvons observer que la valeur du nœud racine est de 15, ce qui est supérieur à la valeur de tous les nœuds du sous-arbre de gauche. La valeur du nœud racine est inférieure aux valeurs de tous les nœuds d'un sous-arbre droit. Passons maintenant au fils gauche du nœud racine. 10 est supérieur à 8 et inférieur à 12 ; il satisfait également à la propriété de l'arbre de recherche binaire. Passons maintenant au fils droit du nœud racine ; la valeur 20 est supérieure à 17 et inférieure à 25 ; il satisfait également à la propriété de l'arbre de recherche binaire. Par conséquent, nous pouvons dire que l’arbre présenté ci-dessus est l’arbre de recherche binaire.

Maintenant, si nous changeons la valeur de 12 en 16 dans l'arbre binaire ci-dessus, nous devons déterminer s'il s'agit toujours d'un arbre de recherche binaire ou non.

point java

La valeur du nœud racine est 15, ce qui est supérieur à 10 mais inférieur à 16, il ne satisfait donc pas à la propriété de l'arbre de recherche binaire. Il ne s’agit donc pas d’un arbre de recherche binaire.

Opérations sur l'arbre de recherche binaire

Nous pouvons effectuer des opérations d'insertion, de suppression et de recherche sur l'arbre de recherche binaire. Comprenons comment une recherche est effectuée sur une recherche binaire. L'arbre binaire est présenté ci-dessous sur lequel nous devons effectuer l'opération de recherche :

Supposons que nous devions rechercher 10 dans l’arbre binaire ci-dessus. Pour effectuer la recherche binaire, nous considérerons tous les entiers d’un tableau trié. Tout d’abord, nous créons une liste complète dans un espace de recherche, et tous les numéros existeront dans l’espace de recherche. L'espace de recherche est marqué par deux pointeurs, c'est-à-dire début et fin. Le tableau de l’arbre binaire ci-dessus peut être représenté comme

Tout d’abord, nous allons calculer l’élément du milieu et comparer l’élément du milieu avec l’élément à rechercher. L'élément du milieu est calculé en utilisant n/2. La valeur de n est 7 ; par conséquent, l'élément du milieu est 15. L'élément du milieu n'est pas égal à l'élément recherché, c'est-à-dire 10.

Remarque : Si l'élément recherché est inférieur à l'élément central, la recherche sera effectuée dans la moitié gauche ; sinon, la recherche se fera sur la moitié droite. En cas d'égalité, l'élément est trouvé.

Comme l'élément à rechercher est inférieur à l'élément médian, la recherche sera effectuée sur le tableau de gauche. Désormais, la recherche est réduite de moitié, comme indiqué ci-dessous :

L'élément médian du tableau de gauche est 10, ce qui est égal à l'élément recherché.

date locale java

Complexité temporelle

Dans une recherche binaire, il y a n éléments. Si l'élément du milieu n'est pas égal à l'élément recherché, alors l'espace de recherche est réduit à n/2, et nous continuerons à réduire l'espace de recherche de n/2 jusqu'à ce que nous trouvions l'élément. Dans toute la réduction, si l’on passe de n à n/2 à n/4 et ainsi de suite, alors il faudra log₂n étapes.

Différences entre l'arbre binaire et l'arbre de recherche binaire