Dans cet article, nous aborderons l'arbre de recherche binaire. Cet article sera très utile et informatif pour les étudiants ayant une formation technique car il s'agit d'un sujet important de leur cours.
Avant de passer directement à l'arbre de recherche binaire, voyons d'abord une brève description de l'arbre.
Qu'est-ce qu'un arbre ?
Un arbre est une sorte de structure de données utilisée pour représenter les données sous forme hiérarchique. Il peut être défini comme un ensemble d'objets ou d'entités appelés nœuds qui sont liés entre eux pour simuler une hiérarchie. L'arbre est une structure de données non linéaire car les données d'un arbre ne sont pas stockées de manière linéaire ou séquentielle.
Maintenant, commençons le sujet, l'arborescence de recherche binaire.
Qu’est-ce qu’un arbre de recherche binaire ?
Un arbre de recherche binaire suit un certain ordre pour organiser les éléments. Dans un arbre de recherche binaire, la valeur du nœud gauche doit être inférieure à celle du nœud parent et la valeur du nœud droit doit être supérieure à celle du nœud parent. Cette règle est appliquée récursivement aux sous-arbres gauche et droit de la racine.
Comprenons le concept d'arbre de recherche binaire avec un exemple.
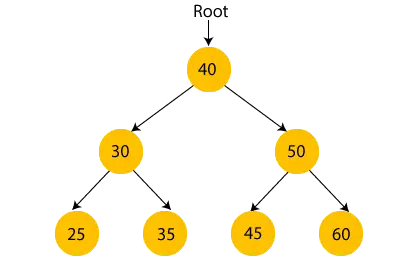
Dans la figure ci-dessus, nous pouvons observer que le nœud racine est 40, et que tous les nœuds du sous-arbre gauche sont plus petits que le nœud racine, et que tous les nœuds du sous-arbre droit sont plus grands que le nœud racine.
De même, nous pouvons voir que l’enfant gauche du nœud racine est plus grand que son enfant gauche et plus petit que son enfant droit. Ainsi, il satisfait également à la propriété de l’arbre de recherche binaire. Par conséquent, nous pouvons dire que l’arbre dans l’image ci-dessus est un arbre de recherche binaire.
Supposons que si nous changeons la valeur du nœud 35 en 55 dans l'arborescence ci-dessus, vérifions si l'arborescence sera un arbre de recherche binaire ou non.

Dans l'arbre ci-dessus, la valeur du nœud racine est 40, ce qui est supérieur à son enfant gauche 30 mais inférieur à son enfant droit de 30, c'est-à-dire 55. Ainsi, l'arbre ci-dessus ne satisfait pas à la propriété de l'arbre de recherche binaire. Par conséquent, l’arbre ci-dessus n’est pas un arbre de recherche binaire.
Avantages de l'arbre de recherche binaire
- La recherche d'un élément dans l'arbre de recherche binaire est facile car nous avons toujours une indication du sous-arbre contenant l'élément souhaité.
- Par rapport aux tableaux et aux listes chaînées, les opérations d'insertion et de suppression sont plus rapides dans BST.
Exemple de création d'un arbre de recherche binaire
Voyons maintenant la création d'un arbre de recherche binaire à l'aide d'un exemple.
Supposons que les éléments de données soient - 45, 15, 79, 90, 10, 55, 12, 20, 50
chaîne dans un tableau en c
- Il faut d’abord insérer Quatre cinq dans l'arbre en tant que racine de l'arbre.
- Ensuite, lisez l’élément suivant ; s'il est plus petit que le nœud racine, insérez-le comme racine du sous-arbre de gauche et passez à l'élément suivant.
- Sinon, si l'élément est plus grand que le nœud racine, insérez-le comme racine du sous-arbre droit.
Voyons maintenant le processus de création de l'arborescence de recherche binaire à l'aide de l'élément de données donné. Le processus de création du BST est illustré ci-dessous -
Étape 1 - Insérez 45.

Étape 2 - Insérez 15.
Comme 15 est inférieur à 45, insérez-le comme nœud racine du sous-arbre gauche.

Étape 3 - Insérez 79.
Comme 79 est supérieur à 45, insérez-le donc comme nœud racine du sous-arbre droit.

Étape 4 - Insérez 90.
âge de Salman Khan Khan
90 est supérieur à 45 et 79, il sera donc inséré comme sous-arbre droit de 79.

Étape 5 - Insérez 10.
10 est plus petit que 45 et 15, il sera donc inséré comme sous-arbre gauche de 15.

Étape 6 - Insérez 55.
55 est supérieur à 45 et inférieur à 79, il sera donc inséré comme sous-arbre gauche de 79.

Étape 7 - Insérez 12.
12 est inférieur à 45 et 15 mais supérieur à 10, il sera donc inséré comme sous-arbre droit de 10.

Étape 8 - Insérez 20.
20 est inférieur à 45 mais supérieur à 15, il sera donc inséré comme sous-arbre droit de 15.

Étape 9 - Insérez 50.
50 est supérieur à 45 mais inférieur à 79 et 55. Il sera donc inséré comme sous-arbre gauche de 55.

La création de l’arbre de recherche binaire est désormais terminée. Après cela, passons aux opérations pouvant être effectuées sur l'arbre de recherche binaire.
Nous pouvons effectuer des opérations d'insertion, de suppression et de recherche sur l'arbre de recherche binaire.
Comprenons comment une recherche est effectuée sur un arbre de recherche binaire.
Recherche dans l'arbre de recherche binaire
Rechercher signifie trouver ou localiser un élément ou un nœud spécifique dans une structure de données. Dans l'arbre de recherche binaire, la recherche d'un nœud est facile car les éléments de BST sont stockés dans un ordre spécifique. Les étapes de recherche d'un nœud dans l'arborescence de recherche binaire sont répertoriées comme suit :
- Commencez par comparer l’élément à rechercher avec l’élément racine de l’arborescence.
- Si root correspond à l’élément cible, renvoie l’emplacement du nœud.
- S'il ne correspond pas, vérifiez si l'élément est inférieur à l'élément racine, s'il est plus petit que l'élément racine, puis déplacez-vous vers le sous-arbre de gauche.
- S'il est plus grand que l'élément racine, déplacez-vous vers le sous-arbre de droite.
- Répétez la procédure ci-dessus de manière récursive jusqu'à ce que la correspondance soit trouvée.
- Si l'élément n'est pas trouvé ou n'est pas présent dans l'arborescence, retournez NULL.
Maintenant, comprenons la recherche dans l'arbre binaire à l'aide d'un exemple. Nous prenons l'arbre de recherche binaire formé ci-dessus. Supposons que nous devions trouver le nœud 20 dans l’arborescence ci-dessous.
Étape 1:

Étape 2:

Étape 3:

Voyons maintenant l'algorithme pour rechercher un élément dans l'arborescence de recherche binaire.
Algorithme pour rechercher un élément dans l'arbre de recherche binaire
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Sortir
programme python pour la recherche binaire
Après l'exécution du code ci-dessus, le résultat sera -

Donc, c'est tout à propos de l'article. J'espère que l'article vous sera utile et informatif.
