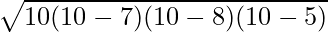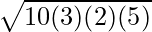Un triangle à angles aigus est un triangle dans lequel tous les angles des triangles sont des angles aigus. Un triangle ne peut avoir qu'un seul angle, soit un angle droit, soit un angle obtus en raison de la propriété de somme des angles du triangle. Et par conséquent, le triangle ayant les trois angles comme angles aigus, c'est-à-dire des angles ayant une valeur inférieure à 90 degrés, est appelé triangle à angle aigu.

En fonction des types d'angles intérieurs du triangle, un triangle peut être classé en trois catégories : triangles à angle aigu, triangles à angle obtus et triangles à angle droit. Apprenons maintenant plus en détail les triangles à angle aigu, leurs types, leurs propriétés et autres dans cet article.

Qu'est-ce qu'un triangle à angle aigu ?

Un triangle à angle aigu est défini comme un triangle dont les trois angles intérieurs sont aigus, c'est-à-dire que leur valeur est comprise entre 0° et 90°. Selon le type de triangle, les longueurs des côtés d'un triangle à angle aigu peuvent être égales ou inégales. Un triangle à angle aigu suit également la propriété de somme des angles du triangle.

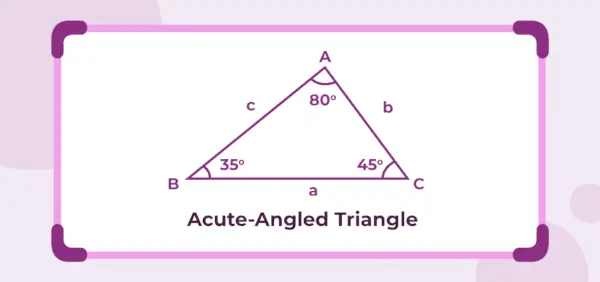
La figure ci-dessous est un triangle à angle aigu dont les angles intérieurs sont 45°, 35° et 80°. Puisque les trois angles intérieurs sont inférieurs à 90°, le triangle donné est un triangle à angle aigu.

Définition du triangle à angle aigu

Les triangles à angles aigus sont définis, comme leur nom l'indique, comme des triangles dans lesquels les trois angles du triangle sont des angles aigus. Le côté des triangles à angle aigu peut être égal ou inégal et, sur cette base, ils sont divisés en trois parties qui sont discutées dans l'article ci-dessous,

Types de triangles à angle aigu

Les triangles à angle aigu sont classés en trois types en fonction de la longueur des côtés des triangles,

• Triangle aigu équilatéral
• Triangle aigu isocèle
• Triangle aigu scalène

Apprenons-en maintenant davantage à leur sujet en détail.

Triangle aigu équilatéral

Un triangle aigu équilatéral également appelé triangle équilatéral est un triangle dans lequel tous les angles sont des angles aigus et tous les angles sont égaux et les côtés des triangles aigus équilatéraux sont également égaux. Chaque angle d'un triangle aigu équilatéral mesure toujours 60°.

Triangle aigu isocèle

Un triangle aigu isocèle est un triangle dans lequel tous les angles sont des angles aigus et deux angles quelconques du triangle et le côté correspondant à ces angles sont égaux. C'est-à-dire que dans le triangle aigu isocèle, nous avons deux côtés et leurs angles correspondants égaux.

Triangle aigu scalène

Un triangle scalène aigu est un triangle dans lequel tous les angles sont des angles aigus et aucun angle ni deux côtés ne sont égaux. C'est-à-dire que dans le triangle scalène aigu, nous n'avons ni côtés ni angles égaux.

Propriétés du triangle à angle aigu

Voici quelques propriétés importantes d'un triangle à angle aigu,

• Les angles intérieurs du triangle à angle aigu sont des angles aigus, c'est-à-dire que les angles sont supérieurs à 0° mais inférieurs à 90°.
• Les angles intérieurs des triangles à angle aigu suivent la propriété de somme des angles, c'est-à-dire que la somme des angles du triangle à angle aigu est de 180°.
• Un triangle équilatéral est toujours un triangle à angle aigu puisque chaque angle intérieur d'un triangle équilatéral mesure 60°.
• Un triangle ne peut pas être à la fois un triangle rectangle et un triangle aigu.
• Un triangle ne peut pas être à la fois un triangle à angle aigu et un triangle à angle obtus.
• Dans le triangle à angle aigu, le côté opposé au plus petit angle est le plus petit et sa réciproque est également vraie.
• De même, le côté opposé au plus grand angle est le plus grand et l’inverse est également vrai.

Formules de triangle à angle aigu

L'aire et le périmètre sont les deux formules de base d'un triangle à angle aigu qui sont discutées ci-dessous.

Périmètre du triangle à angle aigu

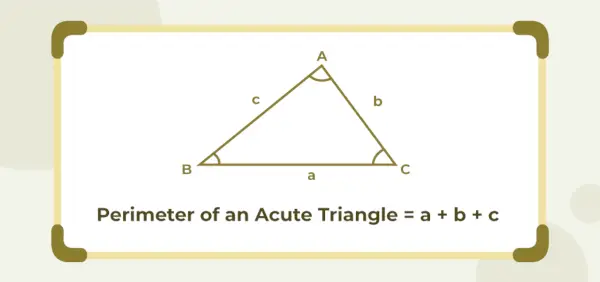
Le périmètre d’un triangle à angle aigu est égal à la somme de ses trois longueurs de côtés. Si a, b et c sont les longueurs des côtés d’un triangle à angle aigu, alors son périmètre est donné en unités (a + b + c).

Périmètre du triangle à angle aigu = (a + b + c) unités

Où un , b , et c sont les longueurs des côtés du triangle.

En savoir plus, Périmètre d'un triangle

Aire du triangle à angle aigu

L'aire d'un triangle est définie comme l'espace total délimité par les trois côtés de tout triangle dans un plan bidimensionnel.

impression java

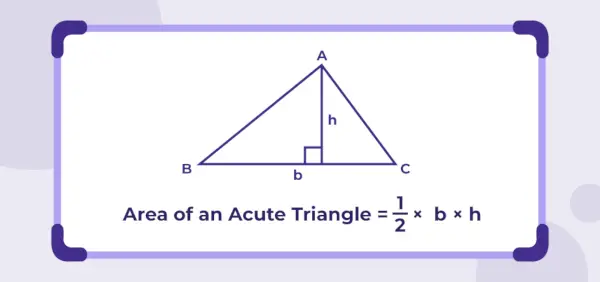
Aire du triangle à angle aigu = ½ × b × h

Où,

b est la longueur de la base et h est la hauteur du triangle.

En savoir plus, Aire d'un triangle

Zone du triangle aigu selon la formule de Heron

Si les trois longueurs des côtés d’un triangle à angle aigu sont données, alors son aire peut être calculée à l’aide de la formule de Heron.

Aire du triangle à angle aigu =

Où,

s est le demi-périmètre et s = (une + b + c)/2 , toi , b , et c sont les longueurs des côtés du triangle.

En savoir plus, La formule du héron

Terminologies importantes du triangle

Les différentes terminologies liées au triangle à angle aigu sont,

Autour du centre

Le centre du cercle qui passe par les trois sommets du triangle est appelé le centre circonscrit du triangle. Il est calculé en prenant le point d’intersection de la médiatrice. Pour un triangle à angle aigu, le centre circonscrit se trouve toujours à l’intérieur du triangle.

Au centre

Le centre du cercle qui touche les trois côtés du triangle est appelé centre du triangle. Il est calculé en prenant le point d'intersection de la bissectrice angulaire. Pour un triangle à angle aigu, le centre se trouve toujours à l’intérieur du triangle.

Centre de gravité

L’intersection des médianes d’un triangle s’appelle le centre de gravité du triangle. Pour un triangle à angle aigu, le centre de gravité du triangle se trouve toujours à l'intérieur du triangle.

Orthocentre

Le point d’intersection des altitudes du triangle est appelé orthocentre du triangle. Pour un triangle à angle aigu, l’orthocentre du triangle se trouve toujours à l’intérieur du triangle.

Exemples résolus sur un triangle à angle aigu

Exemple 1 : Lequel des angles suivants peut former un triangle à angle aigu ?

a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°

Solution:

Nous savons que tous les angles du triangle à angle aigu sont des angles aigus, c'est-à-dire que leur mesure est inférieure à 90 degrés.

Ils suivent également la propriété de somme des angles d’un triangle, c’est-à-dire que tous leurs angles totalisent 180 degrés.

un) 65°, 75°, 50°

Ici, tous les angles sont des angles aigus mais cela ne suit pas la propriété de somme des angles donc le triangle n'est pas possible.

65°+ 75°+ 50° = 190° (Triangle impossible)

b) 95°, 40°, 45°

Ici, le triangle est possible, car il suit la propriété de la somme des angles du triangle, c'est-à-dire

95°+ 40°+ 45° = 180

Mais en observant les angles du triangle nous avons trouvé un angle obtus de 95°. Le triangle n’est donc pas un triangle à angle aigu.

c) 70°,40°,70°

Ici, le triangle est possible, car il suit la propriété de la somme des angles du triangle, c'est-à-dire

70°+ 40°+ 70° = 180

Et en observant les angles du triangle, nous avons constaté que tous les angles sont des angles aigus. Le triangle est donc un triangle à angle aigu.

d) 90°, 45°, 45°

Ici, le triangle est possible, car il suit la propriété de la somme des angles du triangle, c'est-à-dire

90°+ 45°+ 45° = 180

Mais en observant les angles du triangle nous avons trouvé un angle droit de 90°. Le triangle n’est donc pas un triangle à angle aigu.

Exemple 2 : Trouvez le périmètre d'un triangle aigu XYZ dont les côtés sont XY = 8 unités, YZ = 5 unités et XZ = 9 unités.

Solution:

Donné,

Côtés du triangle à angle aigu,

• XY(x) = 8 unités
• YZ(y) = 5 unités
• XZ(z) = 9 unités

Nous savons que,

Périmètre du triangle à angle aigu (P) = x + y + z

⇒ P = (8 + 5 + 9) unités

⇒ P = 22 unités

Le périmètre du triangle à angle aigu est donc de 22 unités.

Exemple 3 : Trouvez l'aire d'un triangle aigu dont la hauteur est de 12 unités et la base est de 15 unités.

Solution:

Donné,

• Hauteur du triangle (h) = 12 unités
• Longueur de la base du triangle (b) = 15 unités

Nous savons que,

Aire du triangle (A) = ½ × b × h

⇒ UNE = ½ × 12 × 15

⇒ A = ½ × 180

⇒ A = 90 unités carrées.

Par conséquent, l’aire du triangle aigu donné est de 90 unités carrées.

Exemple 4 : Trouvez l'aire d'un triangle aigu dont les côtés sont AB = 5 cm, BC = 7 cm et AC = 8 cm.

Solution:

Donné,

Côtés du triangle à angle aigu,

• AB = c = 5 unités
• BC = a = 7 unités
• CA = b = 8 unités

Nous savons que,

Aire du triangle =

⇒ UNE =

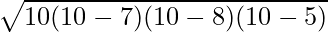
⇒ UNE =

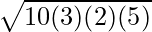
⇒ A = √(300) cm²

⇒ A = 10√3 cm²

Par conséquent, l’aire du triangle aigu donné est de 10√3 cm².

FAQ sur le triangle à angle aigu

Q1 : Que sont les angles aigus ?

Répondre:

Les angles compris entre 0° et 90° sont appelés angles aigus. C'est-à-dire que la valeur minimale de l'angle aigu est supérieure à 0° et que la valeur maximale de l'angle aigu est supérieure à 90°.

Q2 : Qu'est-ce qu'un triangle à angle aigu ?

Répondre:

Un triangle à angle aigu est un triangle dont les trois angles intérieurs sont des angles aigus, c'est-à-dire que la valeur de l'angle est comprise entre 0° et 90°.

Q3 : Un triangle équilatéral est-il toujours un triangle à angle aigu ?

Répondre:

Oui, un triangle équilatéral est toujours un triangle à angle aigu. Les triangles à angles aigus sont les angles dont tous les angles ont des angles aigus, et dans le triangle euqilatéral, tous les angles sont de 60°, c'est-à-dire des angles aigus. Un triangle équilatéral est donc toujours un triangle à angle aigu.

Q4 : Quels sont les différents types de triangles à angle aigu ?

Répondre:

Les triangles à angles aigus sont classés en trois types :

• Triangle aigu scalène
• Triangle aigu isocèle
• Triangle aigu équilatéral

Q5 : Comment savoir si un triangle est un triangle à angle aigu ?

Répondre:

Un triangle dont les angles internes sont inférieurs à 90°, c'est à dire que tous les angles intérieurs sont des angles aigus alors le triangle est appelé triangle à angle aigu. Nous pouvons vérifier si le triangle est un triangle à angle aigu en observant simplement les angles du triangle.