UN Comptoir est un appareil qui stocke (et parfois affiche) le nombre de fois qu'un événement ou un processus particulier s'est produit, souvent en relation avec un signal d'horloge. Les compteurs sont utilisés dans l'électronique numérique à des fins de comptage, ils peuvent compter des événements spécifiques se produisant dans le circuit. Par exemple, dans le compteur UP, un compteur augmente le nombre à chaque front montant de l'horloge. En plus de compter, un compteur peut suivre une certaine séquence basée sur notre conception comme n'importe quelle séquence aléatoire 0,1,3,2…. Ils peuvent également être conçus à l'aide de tongs. Ils sont utilisés comme diviseurs de fréquence où la fréquence d'une forme d'onde d'impulsion donnée est divisée. Les compteurs sont des circuits séquentiels qui comptent le nombre d'impulsions, qui peuvent être sous forme de code binaire ou BCD. Les principales propriétés d'un compteur sont le timing, le séquençage et le comptage. Le compteur fonctionne selon deux modes
Compteur
Compteur descendant
Classement des compteurs
Les compteurs sont globalement divisés en deux catégories
- Compteur asynchrone
- Compteur synchrone
1. Compteur asynchrone
Dans le compteur asynchrone, nous n'utilisons pas d'horloge universelle, seule la première bascule est pilotée par l'horloge principale et l'entrée d'horloge du reste de la bascule suivante est pilotée par la sortie des bascules précédentes. Nous pouvons le comprendre en suivant le schéma-
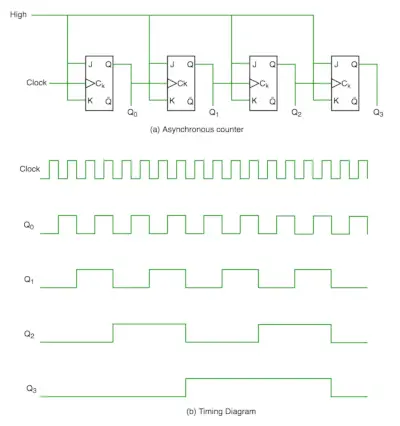
Il ressort clairement du chronogramme que Q0 change dès que le front montant de l'impulsion d'horloge est rencontré, Q1 change lorsque le front montant de Q0 est rencontré (car Q0 est comme l'impulsion d'horloge pour la deuxième bascule) et ainsi de suite. De cette façon, les ondulations sont générées via Q0, Q1, Q2, Q3, c'est pourquoi on les appelle également Compteur RIPPLE et compteur série. Un compteur d'ondulations est un agencement en cascade de bascules où la sortie d'une bascule pilote l'entrée d'horloge de la bascule suivante.
2. Compteur synchrone
Contrairement au compteur asynchrone, le compteur synchrone possède une horloge globale qui pilote chaque bascule afin que la sortie change en parallèle. Le seul avantage du compteur synchrone par rapport au compteur asynchrone est qu'il peut fonctionner à une fréquence plus élevée que le compteur asynchrone car il n'a pas de retard cumulé car la même horloge est donnée à chaque bascule. On l'appelle également compteur parallèle.
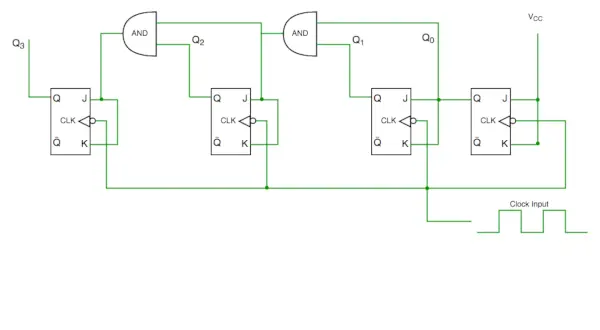
Circuit compteur synchrone
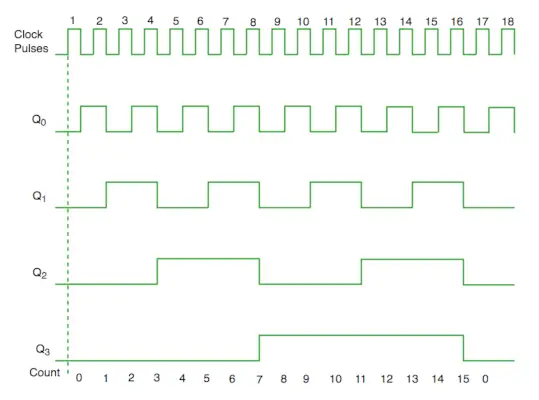
Chronogramme compteur synchrone
D'après le schéma de circuit, nous voyons que le bit Q0 donne une réponse à chaque front descendant de l'horloge tandis que Q1 dépend de Q0, Q2 dépend de Q1 et Q0, Q3 dépend de Q2, Q1 et Q0.
Compteur de décennie
Un compteur décennal compte dix états différents puis est réinitialisé à ses états initiaux. Un simple compteur de décades comptera de 0 à 9 mais nous pouvons également réaliser des compteurs de décades qui peuvent parcourir dix états entre 0 et 15 (pour un compteur 4 bits).
| Impulsion d'horloge | T3 | T2 | T1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| dix | 0 | 0 | 0 | 0 |
Table de vérité pour un simple compteur de dizaines
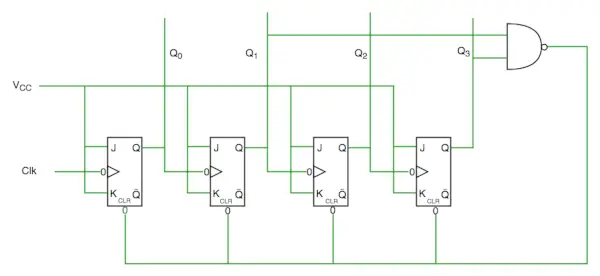
Schéma du circuit du compteur décennal
Nous voyons sur le schéma de circuit que nous avons utilisé la porte NAND pour Q3 et Q1 et que nous l'avons alimenté pour effacer la ligne d'entrée car la représentation binaire de 10 est—
1010
Et nous voyons que Q3 et Q1 valent 1 ici, si nous donnons NAND de ces deux bits pour effacer l'entrée, alors le compteur sera effacé à 10 et recommencera depuis le début.
Point important : Le nombre de bascules utilisées en compteur est toujours supérieur à égal à ( enregistrer2n ) où n=nombre d'états dans le compteur.
Certaines années précédentes soulèvent des questions sur les compteurs
T1. Considérons l'implémentation partielle d'un compteur 2 bits utilisant des bascules T suivant la séquence 0-2-3-1-0, comme indiqué ci-dessous
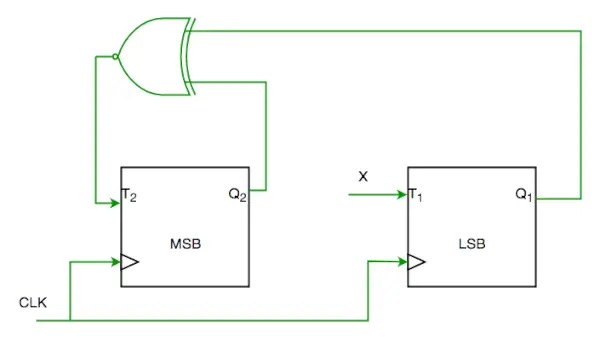
Pour terminer le circuit, l'entrée X doit être
(A) Q2 ?
(B) Q2 + Q1
(C) (Q1 ? Q2)’
(D) Q1 ? T2 (PORTE-CS-2004)
Solution:
Du circuit on voit
T1=XQ1'+X'Q1—-(1)
ET
T2=(Q2 ? Q1)’—-(2)
ET LA SORTIE DÉSIRÉE EST 00->10->11->01->00
DONC X DEVRAIT ÊTRE Q1T2'+Q1'Q2 SATISFAISANT 1 ET 2.
DONC ANS EST (D) PARTIE.
Q2. Les fonctions du signal de commande d'un compteur binaire 4 bits sont données ci-dessous (où X s'en fiche)
Le compteur est connecté comme suit :
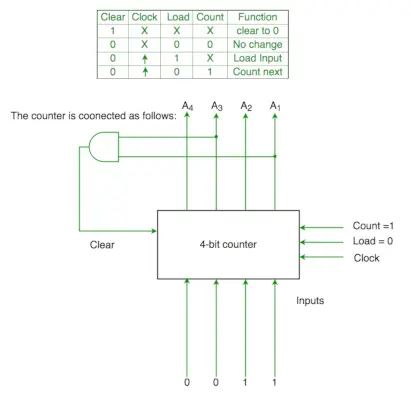
Supposons que les retards des compteurs et des portes soient négligeables. Si le compteur démarre à 0, il parcourt la séquence suivante :
(A)0,3,4
(B)0,3,4,5
(C)0,1,2,3,4
(D)0,1,2,3,4,5 (PORTE-CS-2007)
Solution:
Initialement A1 A2 A3 A4 =0000
Clr=A1 et A3
Ainsi, lorsque A1 et A3 valent tous les deux 1, cela revient à 0000.
Donc 0000(init.) -> 0001(A1 et A3=0)->0010 (A1 et A3=0) -> 0011(A1 et A3=0) -> 0100 ( A1 et A3=1 )(condition claire satisfaite] ->0000(init.) donc ça passe par 0->1->2->3->4
La réponse est la partie (C).
tri des tuples python
Quiz sur la logique numérique
Article rédigé par Anuj Batham,
