L'arbre d'expression est un arbre utilisé pour représenter les différentes expressions. La structure de données arborescente est utilisée pour représenter les instructions expressionnelles. Dans cet arbre, le nœud interne désigne toujours les opérateurs.
- Les nœuds feuilles désignent toujours les opérandes.
- Les opérations sont toujours effectuées sur ces opérandes.
- L’opérateur présent au plus profond de l’arbre est toujours prioritaire.
- L'opérateur, peu présent en profondeur dans l'arbre, est toujours en priorité la plus basse par rapport aux opérateurs situés en profondeur.
- L'opérande sera toujours présent à une profondeur de l'arbre ; c'est pourquoi il est considéré comme le priorité la plus élevée parmi tous les opérateurs.
- Bref, on peut le résumer car la valeur présente en profondeur de l'arbre est la plus prioritaire par rapport aux autres opérateurs présents en haut de l'arbre.
- L’utilité principale de ces arbres d’expression est qu’ils sont utilisés pour évaluer, analyser et modifier les diverses expressions.
- Il est également utilisé pour connaître l'associativité de chaque opérateur dans l'expression.
- Par exemple, l’opérateur + est l’associatif de gauche et / est l’associatif de droite.
- Le dilemme de cette associativité a été résolu grâce à l’utilisation des arbres d’expression.
- Ces arbres d'expression sont formés en utilisant une grammaire sans contexte.
- Nous avons associé une règle en grammaires hors contexte devant chaque production grammaticale.
- Ces règles sont également appelées règles sémantiques, et en utilisant ces règles sémantiques, nous pouvons facilement construire les arbres d'expression.
- C'est l'une des parties majeures de la conception du compilateur et appartient à la phase d'analyse sémantique.
- Dans cette analyse sémantique, nous utiliserons les traductions dirigées par la syntaxe et, sous forme de sortie, nous produirons l'arbre d'analyse annoté.
- Un arbre d'analyse annoté n'est rien d'autre que la simple analyse associée à l'attribut type et à chaque règle de production.
- L'objectif principal de l'utilisation des arbres d'expression est de créer des expressions complexes et peuvent être facilement évaluées à l'aide de ces arbres d'expression.
- Il est immuable, et une fois que nous avons créé un arbre d’expression, nous ne pouvons plus le changer ni le modifier davantage.
- Pour apporter davantage de modifications, il est nécessaire de construire entièrement le nouvel arbre d’expression.
- Il est également utilisé pour résoudre l’évaluation des expressions postfixes, préfixes et infixes.
Les arbres d'expression jouent un rôle très important dans la représentation du niveau de langue code sous forme de données, qui sont principalement stockées dans une structure arborescente. Il est également utilisé dans la représentation mémoire du lambda expression. En utilisant la structure de données arborescente, nous pouvons exprimer l'expression lambda de manière plus transparente et explicite. Il est d'abord créé pour convertir le segment de code en segment de données afin que l'expression puisse être facilement évaluée.
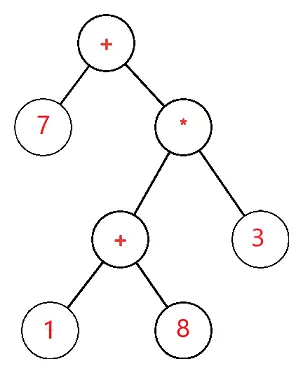
L'arbre d'expression est un arbre binaire dans lequel chaque nœud externe ou feuille correspond à l'opérande et chaque nœud interne ou parent correspond aux opérateurs, donc par exemple l'arbre d'expression pour 7 + ((1+8)*3) serait :
Soit S l'arbre d'expression
Si S n’est pas nul, alors
Si S.value est un opérande, alors
Retourner la valeur S.
x = résoudre (S.gauche)
y = résoudre (S.droite)
Renvoie calculer (x, y, S.value)
Ici, dans l'exemple ci-dessus, l'arbre d'expression utilisait une grammaire sans contexte.
Nous avons quelques productions associées à certaines règles de production dans cette grammaire, principalement connues sous le nom de règles sémantiques . Nous pouvons définir le résultat à partir des règles de production correspondantes en utilisant ces règles sémantiques. Ici, nous avons utilisé le paramètre value, qui calculera le résultat et le renverra au symbole de début de la grammaire. S.left calculera l'enfant gauche du nœud, et de même, l'enfant droit du nœud peut être calculé à l'aide du paramètre S.right.
Utilisation de l'arbre d'expression
- L'objectif principal de l'utilisation des arbres d'expression est de créer des expressions complexes et peuvent être facilement évaluées à l'aide de ces arbres d'expression.
- Il est également utilisé pour connaître l'associativité de chaque opérateur dans l'expression.
- Il est également utilisé pour résoudre l’évaluation des expressions postfixes, préfixes et infixes.
Implémentation d'un arbre d'expression
Pour implémenter l'arbre d'expression et écrire son programme, nous devrons utiliser une structure de données de pile.
Comme nous savons que la pile est basée sur le principe LIFO du dernier entré, premier sorti, l'élément de données récemment inséré dans la pile a été retiré chaque fois que nécessaire. Pour sa mise en œuvre, les deux principales opérations de la pile, push et pop, sont utilisées. En utilisant l'opération push, nous pousserons l'élément de données dans la pile, et en utilisant l'opération pop, nous supprimerons l'élément de données de la pile.
Principales fonctions de la pile dans l'implémentation de l'arbre d'expression :
Tout d'abord, nous allons scanner l'expression donnée de gauche à droite, puis vérifier un par un le caractère identifié,
- Si un caractère scanné est un opérande, nous appliquerons l’opération push et le pousserons dans la pile.
- Si un caractère analysé est un opérateur, nous lui appliquerons l'opération pop pour supprimer les deux valeurs de la pile afin d'en faire son enfant, puis nous repousserons le nœud parent actuel dans la pile.
Implémentation de l'arborescence d'expression en langage de programmation C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Le résultat du programme ci-dessus est :
X + Y * Z / W
Implémentation de l'arborescence d'expression dans le langage de programmation C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Le résultat du programme ci-dessus est :
X + Y * Z / W
Implémentation de l'arborescence d'expression dans le langage de programmation Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 