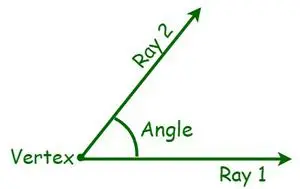
En géométrie, un angle est une mesure essentielle d'une forme géométrique. Un angle est défini comme le degré de rotation autour du point d’intersection entre deux lignes ou plans nécessaires pour mettre l’un en correspondance avec l’autre. Il existe différents types d’angles, basés sur la mesure d’un angle. Elle se mesure en degrés ou en radians. Un angle est une forme formée par deux lignes ou rayons qui divergent d’un point commun appelé sommet. Lorsque deux rayons se coupent, c'est-à-dire lorsque des demi-lignes sont projetées avec une extrémité commune, un angle se forme. Désormais, les extrémités communes sont appelées sommets, tandis que les rayons sont appelés bras.
Types d'angles

- Angle aigu: Un angle aigu est un angle supérieur à 0 degré et inférieur à 90 degrés, c'est-à-dire qu'il va de 0° à 90° (tous deux exclusifs).
- Angle droit: Un angle droit est un angle qui mesure exactement 90 degrés.
- Angle obtus: Un angle obtus est un angle supérieur à 90 degrés et inférieur à 180 degrés, c'est-à-dire qu'il va de 90° à 180° (tous deux exclusifs).
- Angle droit: Un angle droit est un angle qui mesure exactement 180 degrés.
- Angle de réflexion : Un angle réflexe est un angle supérieur à 180 degrés et inférieur à 360 degrés, c'est-à-dire qu'il va de 180° à 360° (tous deux exclusifs).
- Un angle complet ou Rotation Complète : Un angle complet est appelé angle qui mesure exactement 360 degrés.
Il existe également d'autres types d'angles, tels que les angles complémentaires, les angles supplémentaires et les angles adjacents et non adjacents.
- Angles complémentaires: Deux angles sont dits complémentaires si leur somme est un angle droit, soit 90°.
- Angles supplémentaires: Deux angles sont dits supplémentaires si leur somme est égale à 180°.
- Angles adjacents : Deux angles sont dits adjacents s’ils partagent un sommet commun et un bras commun.
- Angles non adjacents : Deux angles sont dits non adjacents s’ils ne partagent pas un sommet commun ni un bras commun.
La formule pour trouver des angles
Il existe différents types de formules pour trouver un angle ; certains d'entre eux sont la formule de l'angle central, la formule du double angle, la formule du demi-angle, la formule de l'angle composé, la formule de l'angle intérieur, etc.
- Nous utilisons la formule de l'angle central pour déterminer l'angle d'un segment formé dans un cercle.
- Nous utilisons la formule de la somme des angles intérieurs pour déterminer l’angle manquant dans un polygone.
- Nous utilisons les rapports trigonométriques pour trouver l'angle manquant d'un triangle rectangle.
- Nous utilisons la loi des sinus ou la loi des cosinus pour trouver l'angle manquant d'un triangle non rectangle.
Nom de la formule | Formule | Comment trouver un angle inconnu ? |
|---|---|---|
| Formule d'angle central | θ =(s × 360°)/2prIci, s est la longueur de l'arc et r est le rayon du cercle | Remplacez les valeurs de longueur de l'arc et de rayon du cercle pour déterminer l'angle d'un segment fait dans un cercle. |
| Somme des angles intérieurs Formule | 180°(n-2)Ici, n est le nombre de côtés d'un polygone | Pour déterminer l'angle intérieur inconnu d'un polygone, calculez d'abord la somme de tous les angles intérieurs à l'aide de cette formule, puis soustrayez la somme de tous les angles connus du résultat. |
| Rapports trigonométriques | sin θ = côté opposé/hypoténusecos θ = adjacent side/hypotenusetan θ = côté opposé/côté adjacent | En fonction des deux côtés disponibles d'un triangle rectangle, choisissez l'un de ces rapports trigonométriques pour trouver l'angle inconnu. |
| Loi des sinus | a/péché A = b/péché B = c/péché CIci A, B et C sont les angles intérieurs d'un triangle et a, b et c sont leurs côtés opposés respectifs. conversion de chaîne en date | Lorsque l’on connaît deux côtés et un angle non inclus (ou) deux angles et un côté non inclus, alors la loi des sinus peut être utilisée pour déterminer les angles inconnus d’un triangle. |
| Loi des cosinus | un2=b2+c2– 2bc cosAb2=c2+ un2– 2ca cosBc2= un2+ b2– 2ab cosCIci A, B et C sont les angles intérieurs d'un triangle et a, b et c sont leurs côtés opposés respectifs. | Lorsque l’on connaît trois côtés (ou) deux côtés et un angle inclus, alors la loi des cosinus peut être utilisée pour déterminer les angles inconnus d’un triangle. |
Exemples de questions
Question 1 : Trouvez l'angle au sommet B du triangle donné en utilisant l'une des formules trigonométriques pour trouver des angles.

Solution:
Donné,
BC = 3 unités = Côté adjacent de θ.
AC = 4 unités = Côté opposé de θ.
Dans ce cas, nous connaissons à la fois les côtés opposés et adjacents de θ. Par conséquent, nous pouvons utiliser la formule de la tangente pour trouver θ.
⇒ tan θ = côté opposé/côté adjacent
⇒ tan θ = 4/3
⇒ θ = bronzage-1(4/3) ⇒ θ = 53,1°
xor cppPar conséquent, l’angle au sommet B est de 53,1°.
Question 2 : Trouvez les angles aux sommets X et Y, si ∠Z = 35° et x = 3 pouces, y = 8 pouces et z = 3,5 pouces.

Solution:
Donné,
∠Z = 35° et x = 6 pouces, y = 3 pouces et z = 3,5 pouces
Puisque nous connaissons les trois côtés et un angle, nous pouvons utiliser la formule de la règle des sinus.
À partir de la formule de la règle sinusoïdale, nous avons
x/péché X = y/péché Y = z/péché Z
Maintenant,
y/péché Y = z/péché Z
⇒ 3/péché Y = 3,5/péché 35°
⇒ 3/sans Y = 3,5/0,574 {Depuis, sin 35° = 0,574}
⇒ péché Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = péché−1(0,492) = 29,47°
Nous savons que la somme de trois angles dans un triangle vaut 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
sont des exemples de modèles⇒ ∠X = 180° – 64,47° = 115,53°
Par conséquent, ∠X = 115,53° et ∠Y = 29,47°.
Question 3 : Calculez le cinquième angle intérieur d'un pentagone si quatre de ses angles intérieurs sont 110°, 85°, 136° et 105°.
Solution:
Le nombre de côtés d'un pentagone (n) = 5.
Maintenant, la somme des 5 angles intérieurs d'un pentagone = 180 (n -2)°
= 180 (5 – 2)° = 540°.
La somme des 4 angles intérieurs donnés = 110°+ 85°+ 136°+ et 105°= 436°.
Donc le cinquième angle intérieur = 540° – 436° = 104°
Ainsi, le cinquième angle intérieur d’un pentagone est de 104°.
Question 4 : Déterminer la valeur de y ainsi que la mesure des angles dans la figure donnée.

Solution:
À partir de la figure donnée, nous pouvons observer que (4y – 6)° et (3y + 5)° sont des angles complémentaires, c'est-à-dire que la somme de (4y – 6)° et (3y + 5)° est 90. °.
⇒ (4a – 6)° + (3a + 5)° = 90°
⇒ (7a – 1)° = 90°
⇒ 7a = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Maintenant, (4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3a + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Question 5 : Trouvez l'angle au sommet Q dans le triangle donné en utilisant l'une des formules pour trouver les angles.

Solution:
Étant donné, p = QR = 6 cm, q = PR = 9 cm et r = PQ = 7 cm.
tronquer et supprimer la différencePuisque nous connaissons les trois côtés et un angle, nous pouvons utiliser la formule de la règle du cosinus pour trouver le sommet de l'angle Q.
⇒ q2=p2+r2– 2pr parce que Q
⇒ 92= 62+ 72– 2 (6)(7) cosQ
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 car Q = 81 – 85
⇒ 84 car Q = -4
⇒ cosQ = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Par conséquent, l'angle au sommet Q, ∠Q = 92,72°.
Question 6 : Calculez l'angle d'un segment fait dans un cercle si la longueur de l'arc est de 12π et le rayon est de 9 cm.
Solution:
Donné,
La longueur de l'arc = 12π
Rayon (r) = 9 cm
Maintenant, la formule de l'angle est :
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
L'angle est donc de 240°.
