- L’opérateur XOR au niveau du bit est également connu sous le nom de OU exclusif
- Il est noté en utilisant le '^'
- Comme son nom l'indique, il fonctionne sur le niveau de bits des opérandes.
- L’opérateur Bitwise XOR entre dans la catégorie des opérateurs Bitwise.
- Dans l'opérateur OU exclusif au niveau du bit (XOR), deux opérandes sont requis et ces deux opérandes sont séparés par le symbole XOR, c'est-à-dire « ^ ».
- Pour déterminer la sortie ou le résultat obtenu après l'application de l'opérateur XOR sur deux opérandes, nous devons suivre la table de vérité logique de l'opérateur XOR.
- XOR Truth Table est la table mathématique construite en utilisant la logique appropriée de l'opérateur XOR.
- La logique utilisée derrière l'opérateur XOR est : chaque fois que l'opération XOR est appliquée sur les deux différent bits de deux opérandes, alors le résultat produira toujours '1', et si l'opération XOR est appliquée sur les deux même bits de deux opérandes, le résultat produit une sortie '0'.
Table de vérité de l'opérateur OU exclusif (XOR)
Supposons qu'il y ait deux opérandes ; le premier est A et le second est B, les combinaisons totales d'entrées formées par ces deux opérandes seront 4. En utilisant la table de vérité XOR suivante, nous déterminerons la sortie correspondante. Le résultat sera capturé en C, ici C = A ^ B.
Dans cette table de vérité, nous prenons les entrées sous forme de bits, c'est-à-dire 0 et 1, et la sortie sera également générée sous forme de bits, c'est-à-dire 0 et 1.
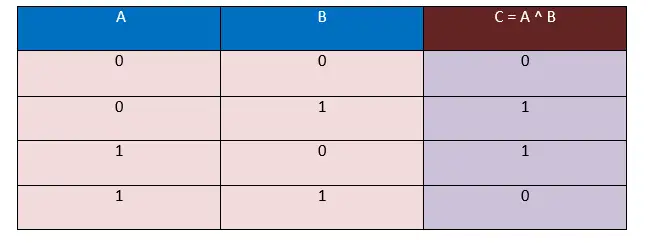
Ici, dans la table de vérité XOR ci-dessus, nous observons que lorsque les valeurs des opérandes A et B sont différentes, c'est-à-dire ( 0, 1 ), ( 1, 0 ), le résultat qui en sort sera toujours 1. Et quand le les valeurs des opérandes A et B sont les mêmes, c'est-à-dire ( 0, 0 ), ( 1, 1 ), le résultat qui en sort sera toujours 0.
De la même façon, nous pouvons tracer la table de vérité pour Booléen valeurs -
Supposons qu'il y ait deux opérandes ; le premier est UN et le deuxième est B . Les combinaisons totales d'entrées formées par ces deux opérandes seront 4. En utilisant la table de vérité XOR suivante, nous déterminerons la sortie correspondante. Le résultat sera capturé en C, ici C = A ^ B.
Dans cette table de vérité, nous prenons les entrées sous la forme de valeurs de vérité, c'est-à-dire Vrai ( T ) et Faux ( F ). La sortie sera également générée sous la forme de valeurs vraies, c'est-à-dire T et F.

Ici, dans la table de vérité XOR ci-dessus, nous observons que, lorsque les valeurs des opérandes A et B sont différentes, c'est-à-dire ( F, T ), ( T, F ), le résultat sera toujours T. Et lorsque le les valeurs des opérandes A et B sont identiques, c'est-à-dire ( F, F ), ( T, T ), le résultat sera toujours F.
D'après les tableaux ci-dessus, nous observons que T ( True ) est noté un et F ( False ) est noté 0.
Étapes pour résoudre un problème donné -
- Les opérandes donnés dans le problème seront toujours en valeur décimale.
- Premièrement, nous devons convertir les valeurs des opérandes en binaire
- Après avoir converti les valeurs des opérandes en nombres binaires, placez les deux opérandes l'un sur l'autre.
- N'oubliez pas qu'avant de leur appliquer une opération OU exclusif (XOR), veuillez vérifier les nombre de chiffres en eux.
- Si le nombre de chiffres ne correspond pas, les 0 supplémentaires à l'extrémité gauche du petit opérande équilibrent le nombre de chiffres.
- Enfin, à l'aide de la table de vérité ci-dessus, appliquez l'opération XOR sur les opérandes un par un, en prenant un bit à la fois pour appliquer l'opération XOR.
- Enfin, le résultat est produit sous forme de sortie.
- La sortie est produite sous forme binaire, convertissez maintenant la forme binaire en forme décimale et notez la valeur du résultat.
Exécution de l'opération Bitwise Exclusive OR (XOR) en C++
Comprenons plus en détail l'exécution de l'opération XOR en C++ à l'aide d'exemples -
Exemple 1 : Trouver le OU exclusif de valeurs entières ; 10 et 14. Expliquez-le également et écrivez le code d'exécution en C++.
Solution: Considérons deux variables, 'a' et 'b', pour stocker les deux opérandes correspondants donnés dans la question ci-dessus, c'est-à-dire 10 et 14.
Ici, a = 10 et b = 14.
Nous suivrons les étapes ci-dessous pour connaître le OU exclusif des deux opérandes donnés.
tutoriel sur le langage de programmation Java
- Nous savons que 10 et 14 sont sous forme décimale, et pour appliquer l'opération XOR au niveau du bit, il est nécessaire de le convertir sous forme binaire.
- Forme binaire « a », c'est-à-dire que 10 est '1010' et Forme binaire de « b », c'est-à-dire que 14 est '1110'.
- Ici, nous observons que le nombre de chiffres binaires présents dans a est de quatre et que le nombre de chiffres binaires présents dans b est également de 4 ; par conséquent, le nombre de chiffres binaires présents dans les deux variables est le même et déjà équilibré, nous n'avons pas besoin d'ajouter plus de 0 pour l'équilibrer.
- Maintenant, mettons les chiffres binaires présents dans « b » par rapport aux chiffres binaires présents dans « a ».
- Enfin, appliquez l’opération XOR un par un sur les bits correspondants et notez le résultat.
- La sortie générée sera enfin sous forme binaire, comme la question ci-dessus donnée sous forme décimale, nous devons donc convertir le résultat sous forme décimale.
Explication:
a = 10 (sous forme décimale)
b = 14 (sous forme décimale)
ajouter une chaîne java
Maintenant, pour un XOR b, nous devons convertir a et b sous forme binaire -
a = 1010 (sous forme binaire)
b = 1110 (sous forme binaire)
Maintenant, en appliquant l'opération XOR sur a et b -
une = 1010
b = 1110
---------------
une ^ b = 0100 (Sous forme binaire)
Le résultat de a ^ b est 0100, qui est sous forme binaire.
Convertissons maintenant le résultat sous forme décimale, qui est 4.
10 ^ 14 = 4
REMARQUE : En utilisant la table de vérité XOR ci-dessus, la sortie des bits correspondants est générée.
Nous allons maintenant appliquer l'opération XOR au niveau du bit sur 10 et 14 en langage C++ et obtenir le résultat, c'est-à-dire 4.
Code C++ pour l'exemple ci-dessus :
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Sortir

Exemple 2 : Trouver le OU exclusif de valeurs entières ; 3 et 15. Expliquez-le également et écrivez le code d'exécution en C++.
Solution: Considérons deux variables, 'a' et 'b', pour stocker les deux opérandes correspondants donnés dans la question ci-dessus, c'est-à-dire 3 et 15.
Ici, a = 3 et b = 15.
comment convertir un entier en chaîne en Java
Nous suivrons les étapes ci-dessous pour connaître le OU exclusif des deux opérandes donnés.
- Nous savons que 3 et 15 sont sous forme décimale, et pour appliquer l'opération XOR au niveau du bit, il est nécessaire de le convertir sous forme binaire.
- Forme binaire ' a ', c'est-à-dire 3 est 'onze' et Forme binaire de « b », c'est-à-dire que 15 est '1111'.
- Ici, nous observerons que le nombre de chiffres binaires présents dans a est de deux et le nombre de chiffres binaires présents dans b est de quatre ; par conséquent, le nombre de chiffres binaires présents dans les deux variables n'est pas le même. Ainsi, en cas de déséquilibre, nous devons ajouter davantage de 0 sur le côté gauche du nombre binaire inférieur, c'est-à-dire a, qui est ' onze' , pour l'équilibrer.
- Après équilibrage, la valeur de a est '0011' , et b est '1111'.
- Maintenant, mettons les chiffres binaires présents dans ' b ' aux chiffres binaires présents dans ' a '.
- Enfin, appliquez l’opération XOR un par un sur les bits correspondants et notez le résultat.
- La sortie générée sera enfin sous forme binaire, comme la question ci-dessus donnée sous forme décimale, nous devons donc convertir le résultat sous forme décimale.
Explication:
a = 3 (sous forme décimale)
b = 15 (sous forme décimale)
Maintenant, pour un XOR b, nous devons convertir a et b sous forme binaire -
a = 0011 (sous forme binaire)
b = 1111 (sous forme binaire)
Maintenant, en appliquant l'opération XOR sur a et b -
'abc' est en chiffres'
une = 0011
b = 1111
---------------
une ^ b = 1100 (Sous forme binaire)
Le résultat de a ^ b est 1100, qui est sous forme binaire.
Convertissons maintenant le résultat sous forme décimale, qui est 12.
3 ^ 15 = 12
REMARQUE : En utilisant la table de vérité XOR ci-dessus, la sortie des bits correspondants est générée.
Nous allons maintenant appliquer l'opération XOR au niveau du bit sur 3 et 15 en langage C++ et obtenir le résultat, c'est-à-dire 12.
Code C++ pour l'exemple ci-dessus :
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Sortir

