Dans cet article, nous discuterons du parcours d'arborescence dans la structure de données. Le terme « traversée d'arbre » signifie traverser ou visiter chaque nœud d'un arbre. Il existe une seule façon de parcourir la structure de données linéaire telle que la liste chaînée, la file d'attente et la pile. Alors qu'il existe plusieurs façons de parcourir un arbre, répertoriées comme suit :
- Parcours des précommandes
- Parcours dans l'ordre
- Traversée des mandats postaux
Ainsi, dans cet article, nous discuterons des techniques énumérées ci-dessus pour parcourir un arbre. Maintenant, commençons à discuter des méthodes de traversée des arbres.
Parcours des précommandes
Cette technique suit la politique « racine gauche droite ». Cela signifie que le premier nœud racine est visité, après quoi le sous-arbre gauche est parcouru de manière récursive, et enfin, le sous-arbre droit est parcouru de manière récursive. Comme le nœud racine est parcouru avant (ou avant) les sous-arbres gauche et droit, cela est appelé parcours de pré-ordre.
Ainsi, dans un parcours de précommande, chaque nœud est visité avant ses deux sous-arbres.
Les applications du parcours de précommande incluent -
- Il est utilisé pour créer une copie de l'arborescence.
- Il peut également être utilisé pour obtenir l’expression de préfixe d’un arbre d’expression.
Algorithme
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Exemple
Voyons maintenant l'exemple de la technique de traversée de précommande.
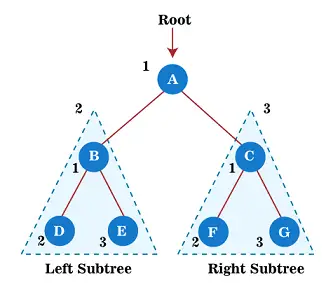
Maintenant, commencez à appliquer le parcours de précommande sur l'arborescence ci-dessus. Tout d'abord, nous traversons le nœud racine UN; après cela, déplacez-vous vers son sous-arbre gauche B , qui sera également parcouru en précommande.
Donc, pour le sous-arbre gauche B, d’abord le nœud racine B est lui-même parcouru; après cela, son sous-arbre gauche D est parcouru. Depuis le nœud D n'a pas d'enfants, déplacez-vous vers le sous-arbre de droite ET . Comme le nœud E n’a pas non plus d’enfants, la traversée du sous-arbre gauche du nœud racine A est terminée.
Java 8
Maintenant, déplacez-vous vers le sous-arbre droit du nœud racine A qui est C. Donc, pour le sous-arbre droit C, commencez par le nœud racine C s'est traversé; après cela, son sous-arbre gauche F est parcouru. Depuis le nœud F n'a pas d'enfants, déplacez-vous vers le sous-arbre de droite g . Comme le nœud G n’a pas non plus d’enfants, la traversée du sous-arbre droit du nœud racine A est terminée.
Ainsi, tous les nœuds de l’arbre sont parcourus. Ainsi, la sortie du parcours de précommande de l'arbre ci-dessus est -
A → B → D → E → C → F → G
Pour en savoir plus sur le parcours de précommande dans la structure de données, vous pouvez suivre le lien Parcours des précommandes .
Traversée des mandats postaux
Cette technique suit la politique de « racine gauche-droite ». Cela signifie que le premier sous-arbre gauche du nœud racine est traversé, puis traverse récursivement le sous-arbre droit et enfin, le nœud racine est traversé. Comme le nœud racine est parcouru après (ou après) les sous-arbres gauche et droit, cela est appelé parcours post-ordre.
Ainsi, dans un parcours post-ordre, chaque nœud est visité après ses deux sous-arbres.
Les applications de la traversée post-commande incluent -
- Il permet de supprimer l'arborescence.
- Il peut également être utilisé pour obtenir l’expression suffixe d’un arbre d’expression.
Algorithme
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Exemple
si sinon sinon si java
Voyons maintenant l'exemple de la technique de traversée post-ordre.

Maintenant, commencez à appliquer le parcours post-ordre sur l’arborescence ci-dessus. Tout d’abord, nous parcourons le sous-arbre gauche B qui sera parcouru en post-ordre. Après cela, nous traverserons le sous-arbre de droite C en post-commande. Et enfin, le nœud racine de l’arbre ci-dessus, c’est-à-dire UN , est parcouru.
Donc, pour le sous-arbre gauche B, d'abord, son sous-arbre gauche D est parcouru. Depuis le nœud D n'a pas d'enfants, parcourez le sous-arbre de droite ET . Comme le nœud E n’a pas non plus d’enfants, passez au nœud racine B. Après avoir traversé le nœud B, la traversée du sous-arbre gauche du nœud racine A est terminée.
protocoles de couche liaison de données
Maintenant, déplacez-vous vers le sous-arbre droit du nœud racine A qui est C. Donc, pour le sous-arbre droit C, d'abord son sous-arbre gauche F est parcouru. Depuis le nœud F n'a pas d'enfants, parcourez le sous-arbre de droite g . Comme le nœud G n'a pas non plus d'enfants, donc finalement, le nœud racine du sous-arbre droit, c'est-à-dire C, est parcouru. La traversée du sous-arbre droit du nœud racine A est terminée.
Enfin, parcourez le nœud racine d'un arbre donné, c'est-à-dire UN . Après avoir traversé le nœud racine, le parcours post-ordre de l'arbre donné est terminé.
Ainsi, tous les nœuds de l’arbre sont parcourus. Ainsi, le résultat du parcours post-ordre de l'arbre ci-dessus est -
D → E → B → F → G → C → A
Pour en savoir plus sur le parcours post-ordre dans la structure de données, vous pouvez suivre le lien Traversée des mandats postaux .
Parcours dans l'ordre
Cette technique suit la politique de « racine gauche droite ». Cela signifie que le premier sous-arbre gauche est visité après la traversée de ce nœud racine, et enfin, le sous-arbre droit est traversé. Lorsque le nœud racine est parcouru entre les sous-arbres gauche et droit, il est nommé parcours dans l'ordre.
Ainsi, dans le parcours dans l'ordre, chaque nœud est visité entre ses sous-arbres.
Les applications de la traversée Inorder comprennent -
- Il est utilisé pour obtenir les nœuds BST par ordre croissant.
- Il peut également être utilisé pour obtenir l’expression de préfixe d’un arbre d’expression.
Algorithme
algèbre booléenne loi distributive
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Exemple
Voyons maintenant l'exemple de la technique de traversée Inorder.

Maintenant, commencez à appliquer le parcours dans l’ordre sur l’arborescence ci-dessus. Tout d'abord, nous parcourons le sous-arbre de gauche B qui sera parcouru dans l'ordre. Après cela, nous traverserons le nœud racine UN . Et enfin, le bon sous-arbre C est parcouru dans l'ordre.
Donc, pour le sous-arbre gauche B , d'abord, son sous-arbre gauche D est parcouru. Depuis le nœud D n'a pas d'enfants, donc après l'avoir parcouru, le nœud B sera parcouru, et enfin, le sous-arbre droit du nœud B, c'est-à-dire ET , est parcouru. Le nœud E n’a pas non plus d’enfants ; par conséquent, la traversée du sous-arbre gauche du nœud racine A est terminée.
Après cela, parcourez le nœud racine d'un arbre donné, c'est-à-dire UN .
Enfin, déplacez-vous vers le sous-arbre droit du nœud racine A qui est C. Donc, pour le sous-arbre droit C ; d'abord, son sous-arbre gauche F est parcouru. Depuis le nœud F n'a pas d'enfants, nœud C sera parcouru, et enfin, un sous-arbre droit du nœud C, c'est-à-dire g , est parcouru. Le nœud G n’a pas non plus d’enfants ; par conséquent, la traversée du sous-arbre droit du nœud racine A est terminée.
Comme tous les nœuds de l’arbre sont parcourus, le parcours dans l’ordre de l’arbre donné est terminé. La sortie du parcours dans l’ordre de l’arbre ci-dessus est -
D → B → E → A → F → C → G
Pour en savoir plus sur le parcours inverse dans la structure de données, vous pouvez suivre le lien Traversée dans l'ordre .
Complexité des techniques de traversée d'arbres
La complexité temporelle des techniques de traversée d'arbres évoquées ci-dessus est Sur) , où 'n' est la taille de l'arbre binaire.
Alors que la complexité spatiale des techniques de traversée d'arbres évoquées ci-dessus est O(1) si nous ne considérons pas la taille de la pile pour les appels de fonction. Sinon, la complexité spatiale de ces techniques est Oh) , où 'h' est la hauteur de l'arbre.
Implémentation de la traversée d'arbres
Voyons maintenant la mise en œuvre des techniques évoquées ci-dessus en utilisant différents langages de programmation.
Programme: Écrivez un programme pour implémenter des techniques de traversée d'arbres en C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Sortir

Programme: Écrivez un programme pour implémenter des techniques de traversée d'arbres en C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Sortir

Programme: Écrivez un programme pour implémenter des techniques de traversée d'arbres en C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Sortir
Après l'exécution du code ci-dessus, le résultat sera -
texte d'habillage CSS

Conclusion
Dans cet article, nous avons discuté des différents types de techniques de parcours d'arbres : parcours pré-ordre, parcours in-ordre et parcours post-ordre. Nous avons vu ces techniques ainsi que l'algorithme, l'exemple, la complexité et l'implémentation en C, C++, C# et Java.
Donc, c'est tout à propos de l'article. J'espère que cela vous sera utile et informatif.
