• L'algorithme Naïve Bayes est un algorithme d'apprentissage supervisé, basé sur Théorème de Bayes et utilisé pour résoudre des problèmes de classification.
• Il est principalement utilisé dans classement du texte qui comprend un ensemble de données de formation de grande dimension.
• Naïve Bayes Classifier est l'un des algorithmes de classification simples et les plus efficaces qui aide à créer des modèles d'apprentissage automatique rapides capables de faire des prédictions rapides.
C'est un classificateur probabiliste, ce qui signifie qu'il prédit sur la base de la probabilité d'un objet.
• Quelques exemples populaires d’algorithme Naïve Bayes sont Filtration du spam, analyse sentimentale et classification des articles .

Pourquoi s’appelle-t-on Naïve Bayes ?

L'algorithme Naïve Bayes est composé de deux mots Naïve et Bayes, qui peuvent être décrits comme :

Naïf: On l'appelle Naïve car il suppose que l'occurrence d'une certaine fonctionnalité est indépendante de l'occurrence d'autres fonctionnalités. Par exemple, si le fruit est identifié sur la base de sa couleur, de sa forme et de son goût, alors le fruit rouge, sphérique et sucré est reconnu comme une pomme. Ainsi, chaque caractéristique contribue individuellement à identifier qu’il s’agit d’une pomme sans dépendre les unes des autres.Bayès: On l'appelle Bayes car il dépend du principe du théorème de Bayes.

Théorème de Bayes :

• Le théorème de Bayes est également connu sous le nom de La règle de Bayes ou Loi de Bayes , qui est utilisé pour déterminer la probabilité d'une hypothèse avec des connaissances préalables. Cela dépend de la probabilité conditionnelle.
• La formule du théorème de Bayes est donnée par :

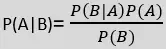
Où,

afficher les applications cachées

P(A|B) est la probabilité postérieure : Probabilité de l'hypothèse A sur l'événement observé B.

P(B|A) est la probabilité de vraisemblance : Probabilité de la preuve étant donné que la probabilité d'une hypothèse est vraie.

P(A) est la probabilité préalable : Probabilité de l'hypothèse avant d'observer les preuves.

P(B) est la probabilité marginale : Probabilité de preuve.

Fonctionnement du classificateur Naïve Bayes :

Le fonctionnement du classificateur Naïve Bayes peut être compris à l'aide de l'exemple ci-dessous :

Supposons que nous ayons un ensemble de données de conditions météorologiques et variable cible correspondante ' Jouer '. Donc, en utilisant cet ensemble de données, nous devons décider si nous devons jouer ou non un jour particulier en fonction des conditions météorologiques. Donc, pour résoudre ce problème, nous devons suivre les étapes ci-dessous :

1. Convertissez l'ensemble de données donné en tableaux de fréquences.
2. Générez un tableau de vraisemblance en recherchant les probabilités de caractéristiques données.
3. Maintenant, utilisez le théorème de Bayes pour calculer la probabilité a posteriori.

Problème : Si le temps est ensoleillé, alors le joueur doit jouer ou pas ?

Solution : Pour résoudre ce problème, considérez d'abord l'ensemble de données ci-dessous :

Tableau de fréquence des conditions météorologiques :

Conditions météorologiques du tableau de probabilité :

1 sur 1000,00

Application du théorème de Bayes :

P(Oui|Ensoleillé)= P(Ensoleillé|Oui)*P(Oui)/P(Ensoleillé)

P(Ensoleillé|Oui)= 3/10= 0,3

P (ensoleillé) = 0,35

P(Oui)=0,71

Donc P(Oui|Ensoleillé) = 0,3*0,71/0,35= 0,60

P(Non|Ensoleillé)= P(Ensoleillé|Non)*P(Non)/P(Ensoleillé)

méthode de sous-chaîne Java

P(Ensoleillé|NON)= 2/4=0,5

P(Non)= 0,29

P (ensoleillé) = 0,35

Donc P(Non|Ensoleillé)= 0,5*0,29/0,35 = 0,41

Ainsi, comme nous pouvons le voir d'après le calcul ci-dessus, P(Oui|Ensoleillé)>P(Non|Ensoleillé)

Ainsi, par une journée ensoleillée, le joueur peut jouer au jeu.

Avantages du classificateur Naïve Bayes :

• Naïve Bayes est l'un des algorithmes de ML rapides et simples permettant de prédire une classe d'ensembles de données.
• Il peut être utilisé pour les classifications binaires et multiclasses.
• Il fonctionne bien dans les prédictions multi-classes par rapport aux autres algorithmes.
• C'est le choix le plus populaire pour problèmes de classification de texte .

Inconvénients du classificateur Naïve Bayes :

• Naive Bayes suppose que toutes les fonctionnalités sont indépendantes ou non liées, il ne peut donc pas apprendre la relation entre les fonctionnalités.

Applications du classificateur Naïve Bayes :

• Il est utilisé pour Notation de crédit .
• Il est utilisé dans classification des données médicales .
• Il peut être utilisé dans prédictions en temps réel parce que Naïve Bayes Classifier est un apprenant avide.
• Il est utilisé dans la classification de texte telle que Filtrage anti-spam et Analyse des sentiments .

Types de modèles naïfs de Bayes :

Il existe trois types de modèles Naive Bayes, indiqués ci-dessous :

Gaussien: Le modèle gaussien suppose que les entités suivent une distribution normale. Cela signifie que si les prédicteurs prennent des valeurs continues au lieu de discrètes, alors le modèle suppose que ces valeurs sont échantillonnées à partir de la distribution gaussienne.Multinomial: Le classificateur Multinomial Naïve Bayes est utilisé lorsque les données sont distribuées multinomiales. Il est principalement utilisé pour les problèmes de classification de documents, cela signifie qu'un document particulier appartient à quelle catégorie, comme le sport, la politique, l'éducation, etc.
Le classificateur utilise la fréquence des mots pour les prédicteurs.Bernoulli: Le classificateur de Bernoulli fonctionne de manière similaire au classificateur multinomial, mais les variables prédictives sont les variables booléennes indépendantes. Comme si un mot particulier est présent ou non dans un document. Ce modèle est également réputé pour les tâches de classification de documents.

Implémentation Python de l'algorithme Naïve Bayes :

Nous allons maintenant implémenter un algorithme Naive Bayes en utilisant Python. Donc pour cela, nous utiliserons le ' données d'utilisateur ' base de données , que nous avons utilisé dans notre autre modèle de classification. On peut donc facilement comparer le modèle Naive Bayes avec les autres modèles.

Étapes à mettre en œuvre :

• Étape de prétraitement des données
• Adaptation de Naive Bayes à l'ensemble de formation
• Prédire le résultat du test
• Test de précision du résultat (Création d'une matrice de confusion)
• Visualisation du résultat de l'ensemble de test.

1) Étape de prétraitement des données :

Dans cette étape, nous allons prétraiter/préparer les données afin de pouvoir les utiliser efficacement dans notre code. C'est similaire à ce que nous avons fait pour le pré-traitement des données. Le code pour cela est donné ci-dessous :

 Importing the libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd # Importing the dataset dataset = pd.read_csv('user_data.csv') x = dataset.iloc[:, [2, 3]].values y = dataset.iloc[:, 4].values # Splitting the dataset into the Training set and Test set from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 0) # Feature Scaling from sklearn.preprocessing import StandardScaler sc = StandardScaler() x_train = sc.fit_transform(x_train) x_test = sc.transform(x_test) 

Dans le code ci-dessus, nous avons chargé l'ensemble de données dans notre programme en utilisant ' ensemble de données = pd.read_csv('user_data.csv') . L'ensemble de données chargé est divisé en ensemble d'entraînement et de test, puis nous avons mis à l'échelle la variable de fonctionnalité.

Le résultat de l'ensemble de données est donné comme suit :

2) Adaptation de Naive Bayes à l'ensemble de formation :

Après l'étape de prétraitement, nous allons maintenant adapter le modèle Naive Bayes à l'ensemble de formation. Ci-dessous le code correspondant :

objet de tableau en Java

 # Fitting Naive Bayes to the Training set from sklearn.naive_bayes import GaussianNB classifier = GaussianNB() classifier.fit(x_train, y_train) 

Dans le code ci-dessus, nous avons utilisé le Classificateur GaussianNB pour l'adapter à l'ensemble de données d'entraînement. Nous pouvons également utiliser d'autres classificateurs selon nos besoins.

Sortir:

qu'est-ce que GB

 Out[6]: GaussianNB(priors=None, var_smoothing=1e-09) 

3) Prédiction du résultat de l'ensemble de test :

Nous allons maintenant prédire le résultat de l’ensemble de test. Pour cela, nous allons créer une nouvelle variable prédictive y_pred , et utilisera la fonction de prévision pour faire les prédictions.

 # Predicting the Test set results y_pred = classifier.predict(x_test) 

Sortir:

La sortie ci-dessus montre le résultat du vecteur de prédiction y_pred et le vecteur réel y_test. Nous pouvons voir que certaines prédictions sont différentes des valeurs réelles, qui sont des prédictions incorrectes.

4) Création d'une matrice de confusion :

Nous allons maintenant vérifier l'exactitude du classificateur Naive Bayes à l'aide de la matrice de confusion. Ci-dessous le code correspondant :

 # Making the Confusion Matrix from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred) 

Sortir:

Comme nous pouvons le voir dans la matrice de confusion ci-dessus, il y a 7+3= 10 prédictions incorrectes et 65+25=90 prédictions correctes.

5) Visualisation du résultat de l'ensemble d'entraînement :

Nous visualiserons ensuite le résultat de l’ensemble de formation à l’aide du classificateur Na�ve Bayes. Ci-dessous le code correspondant :

 # Visualising the Training set results from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Sortir:

Dans le résultat ci-dessus, nous pouvons voir que le classificateur Na�ve Bayes a séparé les points de données avec la limite fine. C'est la courbe gaussienne telle que nous l'avons utilisée GaussienNB classificateur dans notre code.

6) Visualisation du résultat de l'ensemble de tests :

 # Visualising the Test set results from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Sortir:

La sortie ci-dessus est la sortie finale pour les données de l'ensemble de test. Comme nous pouvons le voir, le classificateur a créé une courbe gaussienne pour diviser les variables « achetées » et « non achetées ». Nous avons calculé certaines prédictions erronées dans la matrice de confusion. Mais c’est quand même un très bon classificateur.