Le moment d'inertie est la propriété d'un corps en mouvement de rotation. Le moment d'inertie est la propriété des corps en rotation qui tend à s'opposer au changement de mouvement de rotation du corps. C’est similaire à l’inertie de tout corps en mouvement de translation. Mathématiquement, le moment d'inertie est donné comme la somme du produit de la masse de chaque particule et du carré de la distance à l'axe de rotation. Il est mesuré dans l'unité de kgm 2 .
Apprenons en détail le moment d'inertie dans l'article ci-dessous.
Table des matières
- Définition du moment d'inertie
- Formule du moment d'inertie
- Facteurs affectant le moment d'inertie
- Comment calculer le moment d’inertie ?
- Formule de moment d'inertie pour différentes formes
- Rayon de giration
- Théorèmes du moment d'inertie
- Moments d'inertie pour différents objets
Définition du moment d'inertie
Le moment d'inertie est la tendance d'un corps en mouvement de rotation qui s'oppose au changement de son mouvement rotatif en raison de forces extérieures. Le moment d'inertie se comporte comme une masse angulaire et est appelé inertie de rotation. Le moment d'inertie est analogue au moment d'inertie mécanique Inertie du corps.
Le MOI est défini comme la quantité exprimée par la somme du produit du masse de chaque particule avec le carré de sa distance à l'axe de rotation pour toute particule effectuant le mouvement de rotation.
Unité de moment d'inertie
Le moment d'inertie est une quantité scalaire et l'unité SI du moment d'inertie est kgm 2 .
Formule dimensionnelle du moment d'inertie
Puisque le moment d'inertie est donné comme le produit de la masse et du carré de la distance. C'est formule dimensionnelle est donné par le produit de la formule dimensionnelle de la masse et du carré de la formule dimensionnelle de la longueur. La formule dimensionnelle du moment d'inertie est : ML 2
Qu’est-ce que l’inertie ?
L'inertie est la propriété d'une matière en vertu de laquelle elle tend à résister au changement de l'état de son mouvement. Cela signifie qu'un corps au repos essaie de rester au repos et de résister à toute force essayant de le mettre en mouvement, et qu'un corps en mouvement essaie de continuer son mouvement et de résister à toute force essayant de l'amener à modifier l'ampleur de son mouvement. En termes de quantité, elle est égale à la force maximale essayant de changer son état de mouvement .
En savoir plus sur Inertie .
Formule du moment d'inertie
Le moment d'inertie est un quantité scalaire . Mathématiquement, le produit du carré de la masse d'une particule et de la distance à l'axe de rotation est appelé moment d'inertie de la particule autour de l'axe de rotation.
La formule générale pour trouver le moment d’inertie de n’importe quel objet est la suivante :
je = monsieur 2
où,
m est la masse de l’objet’
r est la distance à l'axe de rotation
Pour un corps constitué de particules continues infinitésimales, la forme intégrale du moment d'inertie est utilisée pour calculer le moment d'inertie.
je = ∫dJe
Je =
int_{0}^{M} r^2 dm
Moment d'inertie d'un système de particules
Le moment d'inertie d'un système de particules est donné par la formule,
je = ∑m je r je 2
où,
r je est la distance perpendiculaire du ièmeparticule de l'axe
m je est la masse de jeèmeparticule
L'équation du moment d'inertie ci-dessus indique que le moment d'inertie d'un système de particules est égal à la somme du produit de la masse de chacune et du carré de la distance à l'axe de rotation de chaque particule.
Pour le chiffre donné ci-dessous,
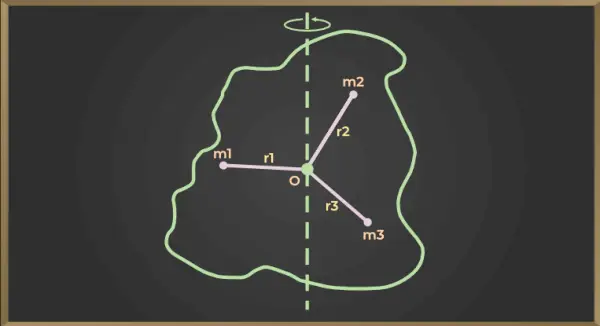
Moment d'inertie de la première particule = m1×r12
Moment d'inertie de la deuxième particule = m2×r22
Moment d'inertie de la troisième particule = m3×r32
De la même manière,
Moment d'inertie de nèmeparticule = mn×rn2
Maintenant le moment d'inertie du corps entier autour de l'axe de rotation UN B sera égal à la somme des moments d'inertie de toutes les particules, donc
je = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
ligne contre colonne
je = Σm je ×r je 2
où,
je représente le moment d'inertie du corps autour de l'axe de rotation
m je est la masse de jeèmeparticule,
r je est le rayon de jeèmeparticule
S représente la somme.
À partir de l’équation, nous pouvons dire que le moment d’inertie d’un corps autour d’un axe fixe est égal à la somme du produit de la masse de chaque particule de ce corps et du carré de sa distance perpendiculaire à l’axe fixe.
Facteurs affectant le moment d'inertie
Le moment d'inertie de tout objet dépend des valeurs suivantes :
- Forme et taille de l'objet
- Densité de la matière de l'objet
- Axe de rotation
Comment calculer le moment d’inertie ?
Plusieurs moyens sont utilisés pour calculer le moment d'inertie de tout objet en rotation.
- Pour les objets uniformes, le moment d'inertie est calculé en prenant le produit de sa masse par le carré de sa distance à l'axe de rotation (r2).
- Pour les objets non uniformes, nous calculons le moment d'inertie en prenant la somme du produit des masses ponctuelles individuelles à chaque rayon différent. Pour cela, la formule utilisée est
je = ∑m je r je 2
Formule de moment d'inertie pour différentes formes
Ce tableau présente les expressions du moment d'inertie de certains objets symétriques ainsi que leur axe de rotation :

| Objet | Axe | Expression du moment d'inertie |
|---|---|---|
| Cylindre creux à paroi mince | Central | Je = Monsieur2 |
| Bague fine | Diamètre | Je = 1/2 Monsieur2 |
| Anneau annulaire ou cylindre creux | Central | je = 1/2 M(r22+r12) |
| Cylindre solide | Central | Je = 1/2 Monsieur2 |
| Disque uniforme | Diamètre | Je = 1/4 Monsieur2 |
| Sphère creuse | Central | Je = 2/3 Monsieur2 |
| Sphère solide | Central | Je = 2/5 Monsieur2 |
| Coque sphérique symétrique uniforme | Central | |
| Plaque uniforme ou parallélépipède rectangulaire | Central | je = 1/12 M(une2+ b2) |
| Tige fine | Central | Je = 1/12 Monsieur2 |
| Tige fine | Au bout du bâton | Je = 1/3 Monsieur2 |
Rayon de giration
Le Rayon de giration d'un corps est défini comme la distance perpendiculaire de l'axe de rotation au point de masse dont la masse est égale à la masse du corps entier et le moment d'inertie est égal au moment d'inertie réel de l'objet tel qu'il a été On suppose que la masse totale du corps y est concentrée. C'est une distance imaginaire. Le rayon de giration est noté K.
Si la masse et le rayon de giration du corps sont respectivement M et K, alors le moment d'inertie d'un corps est
Je = MK 2 ……(1)
Ainsi, le rayon de giration d'un corps est perpendiculaire à l'axe de rotation dont le carré multiplié par la masse de ce corps donne le moment d'inertie de ce corps autour de cet axe.
Encore une fois par l'équation (1), K2= Je/M
K = √(I/m)
Ainsi, le rayon de giration d’un corps autour d’un axe est égal à la racine carrée du rapport du corps autour de cet axe.
Théorèmes du moment d'inertie
Il existe deux types de théorèmes très importants en ce qui concerne le moment d'inertie :
- Théorème des axes parallèles
- Théorème de l'axe perpendiculaire
Théorème de l'axe perpendiculaire
Théorème de l'axe perpendiculaire déclare que la somme du moment d'inertie d'un corps autour de deux axes mutuellement perpendiculaires situés dans le plan d'un corps est égale au moment d'inertie du corps autour du troisième axe qui est perpendiculaire aux deux axes et passe par leur point d'intersection.

Dans la figure ci-dessus, BŒUF et LTD sont deux axes dans le plan du corps qui sont perpendiculaires l'un à l'autre. Le troisième axe est once qui est perpendiculaire au plan du corps et passe par le point d'intersection des BŒUF et LTD axes. Si je X , JE et , et je Avec sont les moments d'inertie du corps autour de l'axe BŒUF , LTD , et once axes respectivement, alors selon ce théorème
je X + je et = je Avec
Théorème des axes parallèles
Selon Théorème de l'axe parallèle , le moment d'inertie d'un corps autour d'un axe donné est la somme du moment d'inertie autour d'un axe passant par le centre de masse de ce corps et le produit du carré de la masse du corps et de la distance perpendiculaire entre le deux axes.

Dans la figure ci-dessus, nous devons trouver le moment d'inertie de je Ô du corps passant par le point Ô et autour de l'axe perpendiculaire au plan, tandis que le moment d'inertie du corps passant par le centre de masse C et autour d'un axe parallèle à l'axe donné est je C , alors d'après ce théorème
je Ô = je C + Ml 2
où
M est la masse de tout le corps
je est la distance perpendiculaire entre deux axes.
Moments d'inertie pour différents objets
Le moment d'inertie de différents objets est discuté ci-dessous dans cet article
Moment d'inertie d'une plaque rectangulaire
Si la masse de la plaque est M, de longueur l et de largeur b, alors le moment d'inertie passe par le centre de gravité et autour d'un axe perpendiculaire au plan de la plaque.
aligner une image en CSS

je = M(l 2 + b 2 / 12)
Moment d'inertie d'un disque
Si le disque a une masse M et un rayon r, alors le moment d’inertie autour de l’axe géométrique du disque est

I = 1/2 (M. 2 )
Moment d'inertie d'une tige
Si la masse de la tige est M et la longueur est l, alors le moment d'inertie autour de l'axe perpendiculaire à la longueur de la tige et passant par son centre de gravité

Je = ML 2 /12
Moment d'inertie d'un cercle
Si la masse de l'anneau est M et le rayon de l'anneau est r, alors le moment d'inertie autour de l'axe passant perpendiculairement au centre de l'anneau est

Je = Monsieur 2
Moment d'inertie d'une sphère
Si une sphère solide a une masse de M et un rayon de r, alors le moment d'inertie autour de son diamètre est

Je = 2/5M. 2
Moment d'inertie du cylindre solide
Le moment d’inertie d’un cylindre solide de rayon « R » et de masse M est donné par

Je = 1/2MR 2
Moment d'inertie du cylindre creux
Un cylindre creux a deux rayons, à savoir le rayon interne et le rayon externe. Le moment d'inertie d'un cylindre creux ayant une masse M et un rayon externe R1, et rayon interne R2est donné comme

je = 1/2M(R 1 2 +R 2 2 )
Moment d'inertie de la sphère solide
Le moment d’inertie d’une sphère solide de masse « M » et de rayon « R » est donné par

I = 2/5MR 2
Moment d'inertie de la sphère creuse
Le moment d’inertie d’une sphère creuse de masse M et de rayon « R » est donné par

Je = 2/3MR 2
Moment d'inertie de l'anneau
Le moment d'inertie d'un anneau est donné pour deux cas où l'axe de rotation passe par le centre et lorsque l'axe de rotation passe par le diamètre.
Le moment d'inertie de l'anneau autour de l'axe passant par le centre est donné par
convertir une chaîne en entier

Je = MR 2
Le moment d'inertie de l'anneau autour de l'axe passant par le diamètre est donné par

Je = Monsieur 2 /2
Moment d'inertie du carré
Le moment d’inertie du carré du côté « a » est donné par

je = un 4 /12
Le moment d’inertie d’une plaque carrée du côté de longueur « l » et de masse M est donné par
Je = 1/6ML 2
Moment d'inertie du triangle
Le moment d'inertie d'un triangle est donné pour 3 situations, premièrement lorsque l'axe passe par le centre, deuxièmement lorsque l'axe passe par la base et troisièmement lorsque l'axe est perpendiculaire à la base. Voyons leur formule une par une. Pour un triangle de base « b » et de hauteur « h », la formule du moment d'inertie est donnée comme suit

Lorsque l'axe passe par le centroïde
Je = bh 3 /36
Lorsque l'axe passe par la base
Je = bh 3 /12
Lorsque l'axe est perpendiculaire à la base
je = (hb/36)(b 2 –b 1 b + b 1 2 )
Différence entre le moment d'inertie et l'inertie
La différence entre l'inertie et le moment d'inertie est présentée ci-dessous :
| Oui Non. | Inertie | Moment d'inertie |
|---|---|---|
| 1. | Son importance réside dans le mouvement linéaire. | Son importance réside dans le mouvement de rotation. |
| 2. | C'est cette propriété d'un objet qui s'oppose au changement d'état de l'objet en mouvement linéaire. | Le moment d'inertie est la propriété d'un objet qui s'oppose au changement d'état de l'objet en mouvement de rotation. |
| 3. | L'inertie d'un objet dépend uniquement de sa masse. | Le moment d'inertie d'un objet dépend de sa masse et de sa répartition de masse par rapport à l'axe de rotation. |
| 4. | L'inertie d'un objet est fixe. | Le moment d'inertie d'un objet varie en fonction des différents axes de rotation. |
Énergie cinétique du corps en rotation
Supposons un corps de masse « m » tournant avec une vitesse v à une distance « r » de l'axe de rotation. Sa vitesse angulaire est alors donnée par ω = v/r alors v = rω. Maintenant nous savons que le Énergie cinétique d'un corps est donné par
KE = 1/2mV 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2Oh2
⇒ KE = 1/2Iω 2
Par conséquent, l’énergie cinétique d’un corps en rotation est donnée par la moitié du produit du moment d’inertie et du vitesse angulaire du corps. L'énergie cinétique d'un corps en rotation est également appelée Énergie cinétique de rotation . La formule de l’énergie cinétique de rotation est donnée par
KE = 1/2Iω 2
Le moment d'inertie (I) est indépendant de la vitesse angulaire du corps. C'est une fonction de la masse du corps en rotation et de la distance du corps à l'axe de rotation. Par conséquent, nous observons que le mouvement angulaire est analogue au mouvement linéaire, cela signifie que la signification du moment d'inertie est qu'il donne une idée de la façon dont les masses sont réparties à différentes distances de l'axe de rotation dans un corps en rotation.
Application du moment d'inertie
Le moment d'inertie a diverses applications, dont certaines sont décrites ci-dessous :
- En raison du moment d'inertie plus grand, la Terre tourne sur son axe avec la même vitesse angulaire.
- Une petite roue mobile est placée sous le moteur de jeu des enfants. Après avoir frotté cette roue avec le sol et quitté le moteur, en raison du moment d'inertie de la roue, le moteur continue de tourner pendant un certain temps.
- Chaque moteur est constitué d'une grande et lourde roue attachée à son arbre, avec la majeure partie de sa masse sur sa circonférence. Son moment d’inertie est donc élevé. Cette roue s'appelle un volant d'inertie. Le couple qui entraîne l’arbre du moteur ne cesse d’augmenter. Par conséquent, la rotation de l’arbre peut ne pas être uniforme, mais en raison de la présence d’une roue mobile avec plus d’inertie, l’arbre continue de tourner à une vitesse presque uniforme.
- Dans la roue des chars à bœufs, des pousse-pousse, des scooters, des cycles, etc., la majeure partie de la masse est concentrée sur son cercle ou jante. cet arceau ou routine est fixé à l'axe de la roue par des rayons rigides. Ce faisant, son moment d'inertie augmente. Ainsi, lorsque les jambes arrêtent de bouger pendant le cyclisme, la roue continue de tourner pendant un certain temps.
Vérifiez également
- Cinématique du mouvement de rotation
- Mouvement d'un corps rigide
- Mouvement de roulement
Exemples résolus sur les moments d'inertie
Exemple 1 : Un corps de masse 500 g tourne autour d'un axe. la distance entre le centre de masse du corps et l'axe de rotation est de 1,2 m. trouver le moment d'inertie du corps autour de l'axe de rotation.
Solution:
Sachant que M = 500 g = 0,5 kg, r = 1,2 m.
Évidemment, on peut supposer que la masse entière d’un corps est placée en son centre de masse. Puis le moment d'inertie du corps autour de l'axe de rotation.
Je = Monsieur2
je = 0,5 × (1,2)2
je = 0,72 kg·m2
Exemple 2 : Le rayon de révolution autour d'un axe situé à 12 cm du centre de masse d'un corps de masse de 1,2 kg est de 13 cm. Calculez le rayon de révolution et moment d'inertie autour d'un axe passant par le centre de masse.
Solution:
Sachant que M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, jeCM= ?
Du théorème de l'axe parallèle I = ICM+ Ml2
K2=KCM2+ l2
comment révéler les applications cachéesou KCM2=K2– je2
KCM2 = (13)2– (12)2= 25
KCM= 5
Maintenant, moment d'inertie ICM= MKCM2
jeCM= 1,0 × (0,05)2= 2,5 × 10-3kgm2
Exemple 3 : Un corps d'une masse de 0,1 kg tourne autour d'un axe. si la distance entre le centre de masse du corps et l'axe de rotation est de 0,5 m, alors trouvez le moment d'inertie du corps.
Solution:
Sachant cela, M = 0,1 kg et r = 0,5 m
donc je = Monsieur2
je = 0,1 × (0,5)2
je = 0,025 kg·m2
Exemple 4 : Le moment d'inertie des anneaux autour d'un axe passant par son centre perpendiculaire au plan de l'anneau circulaire est de 200 gm cm 2 . Quel sera le moment d'inertie par rapport à son diamètre ?
Solution:
Moment d'inertie d'un anneau circulaire autour d'un axe passant par un autre centre perpendiculaire à son plan
M2= 200 g cm2
Moment d'inertie par rapport au diamètre
= 1/2 MR2
= 1/2 × 200 = 100 g cm2
FAQ sur les moments d'inertie
Comment calculer le moment d'inertie ?
La formule de base pour trouver le moment d’inertie de tout objet uniforme est la suivante :
je = monsieur 2
où,
m est la masse de l’objet’
r est la distance à l'axe de rotation
Comment calculer le moment d'inertie d'une poutre ?
Le moment d'inertie d'une poutre le long du centre et de l'axe horizontal par rapport à celle-ci est calculé à l'aide de la formule :
Je = ML 2 / 12
De quoi dépend le moment d’inertie d’un corps ?
Le moment d'inertie de tout objet dépend des facteurs indiqués ci-dessous :
- Masse du Corps,
- Axe de rotation
- Forme et taille de l'objet
Quelle est l'unité du moment d'inertie ?
L'unité du moment d'inertie est KGM 2
Le moment d’inertie peut-il être négatif ?
Non, le moment d’inertie ne peut jamais être négatif.
Qu’est-ce que le moment d’inertie de masse ?
Le moment d'inertie de masse est la mesure de la résistance d'un corps au changement de son moment cinétique ou de sa direction. Le moment d'inertie de masse pour une masse ponctuelle est donné par I = mr2et pour un système de particules, le moment d'inertie de masse est donné par I = Σjemjerje2
Qu’est-ce que le moment d’inertie de l’aire ?
Le moment d'inertie de la zone est la propriété d'un plan de forme 2D qui montre comment les points sont dispersés par rapport à un axe arbitraire dans un plan. Le moment d'inertie de la zone est également connu sous le nom de deuxième moment de la zone ou moment quadratique de la zone. La formule du moment d'inertie de l'aire dans le plan xy est donnée par Ixy= ∫xy dxdxy = ∫xy dA
