La hauteur ou la profondeur d'un arbre binaire peut être définie comme le nombre maximum ou le plus grand nombre d'arêtes d'un nœud feuille au nœud racine ou d'un nœud racine au nœud feuille. Le nœud racine sera au niveau zéro, ce qui signifie que si aucun des nœuds enfants n'est connecté au nœud racine, alors la hauteur ou la profondeur de l'arbre binaire particulier est dite nulle.
Prenons un exemple pour mieux comprendre la hauteur de l'arbre binaire.
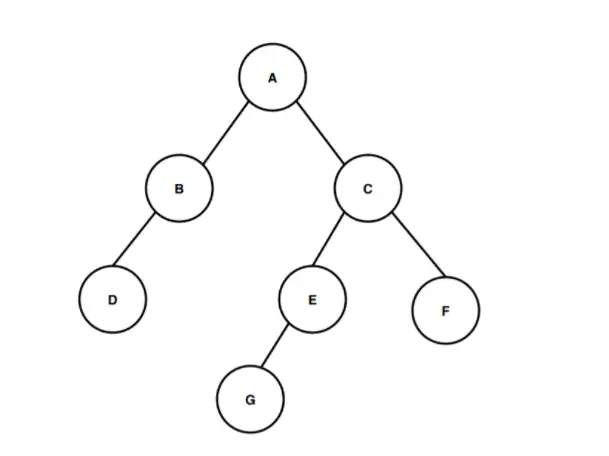
Dans l'image ci-dessus, nous avons un arbre binaire commençant à partir du nœud racine nommé A. Le nœud racine A a respectivement deux nœuds enfants B et C comme enfant gauche et enfant droit. Et de même, le nœud enfant gauche B n'a qu'un seul nœud enfant gauche nommé D et le nœud enfant droit C a deux nœuds enfants E et F à partir desquels le nœud E a le nœud G comme seul enfant gauche.
Déol ensoleillé
Calculons maintenant la hauteur de cet arbre binaire. Comptez le nombre d'arêtes en partant du nœud racine jusqu'au nœud feuille le plus profond pour calculer la hauteur de l'arbre binaire. Le nœud le plus profond présent dans cet arbre binaire est le nœud G. Ainsi, pour le calcul de la hauteur ou de la profondeur de cet arbre binaire, nous devons calculer le nombre d'arêtes entre le nœud racine et le nœud le plus profond G. La première arête va du nœud A au nœud C, la deuxième arête va du nœud C au nœud E et la troisième arête va du nœud E au nœud G. Ainsi, pour passer du nœud racine A au nœud le plus profond G, il y a trois arêtes , donc la hauteur ou la profondeur de l'arbre binaire est 3. Le chemin que nous avons suivi pour passer de la racine au nœud feuille le plus profond est A > C > E > G et ce chemin couvre trois arêtes pendant le parcours, c'est pourquoi selon à la définition de la hauteur de l'arbre binaire la hauteur de cet arbre binaire est 3.
Façons de trouver la hauteur de l’arbre binaire
Maintenant, écrivons du code pour trouver la hauteur d'un arbre binaire. Il existe deux façons de déterminer la hauteur de l’arbre binaire. L'un est le méthode récursive et l'autre est le méthode non récursive qui utilisera la structure de données Queue pour calculer la hauteur de l'arbre binaire.
Manière récursive
Voyons d’abord la manière récursive de trouver la hauteur de l’arbre binaire.
Code:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Sortir: Le résultat du code ci-dessus est :
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
De manière récursive, nous avons appelé le hauteur() fonction à plusieurs reprises pour trouver la hauteur de l’arbre binaire. Le nœud racine de l’arbre binaire est passé en paramètre à la fonction height(). La fonction height() calcule la hauteur des deux sous-arbres du nœud racine et laquelle parmi les deux hauteurs est la plus élevée est considérée comme la hauteur de l'arbre binaire.
caractère de chaîne Java
Méthode non récursive
Voyons maintenant la manière non récursive de trouver la hauteur de l'arbre binaire.
Code:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> Dans cette approche, nous avons utilisé une méthode non récursive pour trouver la profondeur de l'arbre binaire. Pour trouver la hauteur de l'arbre binaire, nous avons écrit une fonction nommée height qui nécessitera un paramètre de type Node (c'est-à-dire la racine de l'arbre binaire dont il faut calculer la hauteur). La racine de l’arbre binaire est présente au niveau zéro, ce qui signifie que la hauteur ou la profondeur de la racine est nulle.
Dans l'approche non récursive, nous utilisons la structure de données de file d'attente pour trouver la profondeur de l'arbre binaire. Les nœuds de l'arbre binaire dont on veut trouver la profondeur sont ajoutés à la structure de données Queue à l'aide d'une opération de mise en file d'attente à laquelle le nœud de l'arbre binaire est passé en paramètre à cette fonction.
Une fois que tous les nœuds sont ajoutés à la file d'attente, les nœuds ajoutés dans la file d'attente sont supprimés en appelant la fonction dequeue qui continuera à supprimer un élément de la file d'attente jusqu'à ce que le nœud nul de l'arbre binaire soit rencontré. Chaque fois qu'un nœud de l'arbre binaire de la file d'attente est supprimé, la variable de profondeur représentant la profondeur de l'arbre binaire est incrémentée de un. Et au final, la valeur de la variable profondeur représentera la profondeur finale de l'arbre binaire.
