Introduction:

Un demi-additionneur est un circuit logique numérique qui effectue l'addition binaire de deux nombres binaires à un seul bit. Il possède deux entrées, A et B, et deux sorties, SUM et CARRY. La sortie SUM est le bit le moins significatif (LSB) du résultat, tandis que la sortie CARRY est le bit le plus significatif (MSB) du résultat, indiquant s'il y a eu un report de l'addition des deux entrées. Le demi-additionneur peut être implémenté à l'aide de portes de base telles que les portes XOR et AND.

Bien sûr, voici une explication plus détaillée du circuit du demi-additionneur :

Le demi-additionneur est un élément de base pour les circuits additionneurs plus complexes tels que les additionneurs complets et les additionneurs à plusieurs bits. Il effectue l'addition binaire de deux entrées à un seul bit, A et B, et fournit deux sorties, SUM et CARRY.

conversion d'une chaîne en entier

La sortie SUM est le bit le moins significatif (LSB) du résultat, qui est le XOR des deux entrées A et B. La porte XOR implémente l'opération d'addition pour les chiffres binaires, où un 1 est généré dans la sortie SUM uniquement lorsqu'un des entrées est 1.

La sortie CARRY est le bit de poids fort (MSB) du résultat, indiquant s'il y a eu un report de l'addition des deux entrées. La sortie CARRY est le ET des deux entrées A et B. La porte ET génère un 1 dans la sortie CARRY uniquement lorsque les deux entrées sont à 1.

Demi-additionneur (HA) :

Le demi-additionneur est le plus simple de tous les circuits additionneurs. Le demi-additionneur est un circuit arithmétique combinatoire qui additionne deux nombres et produit un ou plusieurs bits de somme et un bit de retenue (c) tous deux en sortie. L'addition de 2 bits se fait à l'aide d'un circuit combiné appelé Half additionneur. Les variables d'entrée sont des bits d'augend et d'addend et les variables de sortie sont des bits de somme et de report. A et B sont les deux bits d'entrée.

considérons deux bits d'entrée A et B, alors le ou les bits de somme sont le X-OR de A et B. il ressort clairement de la fonction d'un demi-additionneur qu'il nécessite une porte X-OR et une porte ET pour son construction.

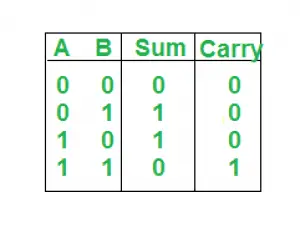
Table de vérité:

Ici, nous effectuons deux opérations Sum et Carry, nous avons donc besoin de deux K-maps, une pour chacune, pour dériver l'expression.

Expression logique :

Pour la somme :

algorithme de tri rapide

Somme = A XOR B

Pour le transport :

Porter = A ET B

Mise en œuvre:

Note: Le demi-additionneur n'a que deux entrées et il n'est pas prévu d'ajouter une retenue provenant des bits d'ordre inférieur lorsque l'addition multiple est effectuée.

Avantages et inconvénients du Half Adder en logique numérique :

Avantages du demi-additionneur en logique numérique :

1.Simplicité : Une demi-vipère est un circuit simple qui nécessite quelques éléments fondamentaux comme les entrées XOR AND. Ce n’est pas difficile à réaliser et peut être utilisé dans de nombreux frameworks avancés.

2.Vitesse : La demi-vipère fonctionne extrêmement rapidement, ce qui la rend raisonnable pour une utilisation dans des circuits informatisés rapides.

Inconvénients du Half Adder en logique numérique :

1.Utilité limitée : La demi-vipère peut ajouter deux numéros d'une seule pièce et produire un total et un bit de transmission. Il ne peut pas effectuer d’expansion de nombres multibits, ce qui nécessite l’utilisation de circuits complexes supplémentaires tels que des additionneurs complets.

2. Manque d'informations de transmission : Le demi-serpent n’a pas d’entrée de transmission, ce qui limite sa valeur dans des tâches d’expansion plus ahurissantes. Une entrée de transmission est importante pour effectuer l’expansion de nombres multi-bits et pour enchaîner de nombreux additionneurs.

quand l'école a-t-elle été inventée

3. Report de propagation : Le circuit demi-serpent a un délai de prolifération, qui est le temps qu'il faut pour que le résultat change suite à un ajustement de l'information. Cela peut entraîner des problèmes de synchronisation dans les circuits informatisés, en particulier dans les cadres rapides.

Application du demi-additionneur dans la logique numérique :

1.Circuits arithmétiques : Les demi-additionneurs sont utilisés dans les circuits de calcul de nombres pour ajouter des nombres doubles. Lorsque différents demi-additionneurs sont associés dans une chaîne, ils peuvent ajouter des nombres doubles multi-bits.

2. Traitement des données : Les demi-additionneurs sont utilisés dans les applications de traitement de l'information telles que la gestion informatisée du signal, le cryptage de l'information et la correction des erreurs.

3. Déroulement de l’adresse : Dans le domaine de la mémoire, des demi-additionneurs sont utilisés dans les circuits de déchiffrement d'adresses pour produire l'emplacement d'une zone de mémoire particulière.

4.Circuits codeurs et décodeurs : Les demi-additionneurs sont utilisés dans les circuits codeurs et décodeurs pour les cadres de correspondance informatisés.

5.Multiplexeurs et démultiplexeurs : Les demi-additionneurs sont utilisés dans les multiplexeurs et les démultiplexeurs pour sélectionner et traiter les informations.

6.Compteurs : Des demi-additionneurs sont utilisés dans les compteurs pour augmenter le décompte de un.