Dans cet article, nous aborderons l'algorithme de tri rapide. La procédure de travail de Quicksort est également simple. Cet article sera très utile et intéressant pour les étudiants, car ils pourraient être confrontés à une question de tri rapide lors de leurs examens. Il est donc important d’aborder le sujet.
Le tri est une manière de disposer les éléments de manière systématique. Quicksort est l'algorithme de tri largement utilisé qui permet n journal n comparaisons dans le cas moyen pour trier un tableau de n éléments. Il s'agit d'un algorithme de tri plus rapide et très efficace. Cet algorithme suit l’approche diviser pour mieux régner. Diviser pour mieux régner est une technique qui consiste à décomposer les algorithmes en sous-problèmes, puis à résoudre les sous-problèmes et à combiner les résultats pour résoudre le problème d'origine.
algorithme de Kruskal
Diviser: Dans Divide, choisissez d’abord un élément pivot. Après cela, divisez ou réorganisez le tableau en deux sous-tableaux de telle sorte que chaque élément du sous-tableau de gauche soit inférieur ou égal à l'élément pivot et que chaque élément du sous-tableau droit soit plus grand que l'élément pivot.
Conquérir: De manière récursive, triez deux sous-tableaux avec Quicksort.
Combiner: Combinez le tableau déjà trié.
Le tri rapide sélectionne un élément comme pivot, puis partitionne le tableau donné autour de l'élément pivot sélectionné. Lors du tri rapide, un grand tableau est divisé en deux tableaux dans lesquels l'un contient les valeurs inférieures à la valeur spécifiée (Pivot) et un autre tableau contient les valeurs supérieures au pivot.
Après cela, les sous-tableaux gauche et droit sont également partitionnés en utilisant la même approche. Cela continuera jusqu'à ce que l'élément unique reste dans le sous-tableau.
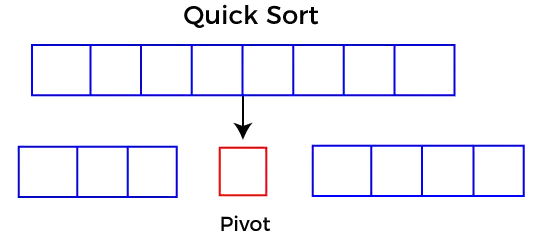
Choisir le pivot
Choisir un bon pivot est nécessaire pour la mise en œuvre rapide du tri rapide. Cependant, il est typique de déterminer un bon pivot. Certaines des façons de choisir un pivot sont les suivantes :
- Le pivot peut être aléatoire, c'est-à-dire sélectionner le pivot aléatoire dans le tableau donné.
- Le pivot peut être l'élément le plus à droite ou l'élément le plus à gauche du tableau donné.
- Sélectionnez la médiane comme élément pivot.
Algorithme
Algorithme:
QUICKSORT (array A, start, end) { 1 if (start <end) 2 3 4 5 6 { p="partition(A," start, end) quicksort (a, - 1) + 1, } < pre> <p> <strong>Partition Algorithm:</strong> </p> <p>The partition algorithm rearranges the sub-arrays in a place.</p> <pre> PARTITION (array A, start, end) { 1 pivot ? A[end] 2 i ? start-1 3 for j ? start to end -1 { 4 do if (A[j] <pivot) 1 5 6 7 8 9 { then i ? + swap a[i] with a[j] }} a[i+1] a[end] return i+1 } < pre> <h2>Working of Quick Sort Algorithm</h2> <p>Now, let's see the working of the Quicksort Algorithm.</p> <p>To understand the working of quick sort, let's take an unsorted array. It will make the concept more clear and understandable.</p> <p>Let the elements of array are -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-2.webp" alt="Quick Sort Algorithm"> <p>In the given array, we consider the leftmost element as pivot. So, in this case, a[left] = 24, a[right] = 27 and a[pivot] = 24.</p> <p>Since, pivot is at left, so algorithm starts from right and move towards left.</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-3.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] <a[right], so algorithm moves forward one position towards left, i.e. -< p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-4.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 24, a[right] = 19, and a[pivot] = 24.</p> <p>Because, a[pivot] > a[right], so, algorithm will swap a[pivot] with a[right], and pivot moves to right, as -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-5.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 19, a[right] = 24, and a[pivot] = 24. Since, pivot is at right, so algorithm starts from left and moves to right.</p> <p>As a[pivot] > a[left], so algorithm moves one position to right as -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-6.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 9, a[right] = 24, and a[pivot] = 24. As a[pivot] > a[left], so algorithm moves one position to right as -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-7.webp" alt="Quick Sort Algorithm"> <p>Now, a[left] = 29, a[right] = 24, and a[pivot] = 24. As a[pivot] <a[left], so, swap a[pivot] and a[left], now pivot is at left, i.e. -< p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-8.webp" alt="Quick Sort Algorithm"> <p>Since, pivot is at left, so algorithm starts from right, and move to left. Now, a[left] = 24, a[right] = 29, and a[pivot] = 24. As a[pivot] <a[right], so algorithm moves one position to left, as -< p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-9.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] = 24, a[left] = 24, and a[right] = 14. As a[pivot] > a[right], so, swap a[pivot] and a[right], now pivot is at right, i.e. -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-10.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] = 24, a[left] = 14, and a[right] = 24. Pivot is at right, so the algorithm starts from left and move to right.</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-11.webp" alt="Quick Sort Algorithm"> <p>Now, a[pivot] = 24, a[left] = 24, and a[right] = 24. So, pivot, left and right are pointing the same element. It represents the termination of procedure.</p> <p>Element 24, which is the pivot element is placed at its exact position.</p> <p>Elements that are right side of element 24 are greater than it, and the elements that are left side of element 24 are smaller than it.</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-12.webp" alt="Quick Sort Algorithm"> <p>Now, in a similar manner, quick sort algorithm is separately applied to the left and right sub-arrays. After sorting gets done, the array will be -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-13.webp" alt="Quick Sort Algorithm"> <h2>Quicksort complexity</h2> <p>Now, let's see the time complexity of quicksort in best case, average case, and in worst case. We will also see the space complexity of quicksort.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Case</th> <th>Time Complexity</th> </tr> <tr> <td> <strong>Best Case</strong> </td> <td>O(n*logn)</td> </tr> <tr> <td> <strong>Average Case</strong> </td> <td>O(n*logn)</td> </tr> <tr> <td> <strong>Worst Case</strong> </td> <td>O(n<sup>2</sup>)</td> </tr> </table> <ul> <tr><td>Best Case Complexity -</td> In Quicksort, the best-case occurs when the pivot element is the middle element or near to the middle element. The best-case time complexity of quicksort is <strong>O(n*logn)</strong> . </tr><tr><td>Average Case Complexity -</td> It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of quicksort is <strong>O(n*logn)</strong> . </tr><tr><td>Worst Case Complexity -</td> In quick sort, worst case occurs when the pivot element is either greatest or smallest element. Suppose, if the pivot element is always the last element of the array, the worst case would occur when the given array is sorted already in ascending or descending order. The worst-case time complexity of quicksort is <strong>O(n<sup>2</sup>)</strong> . </tr></ul> <p>Though the worst-case complexity of quicksort is more than other sorting algorithms such as <strong>Merge sort</strong> and <strong>Heap sort</strong> , still it is faster in practice. Worst case in quick sort rarely occurs because by changing the choice of pivot, it can be implemented in different ways. Worst case in quicksort can be avoided by choosing the right pivot element.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <td> <strong>Space Complexity</strong> </td> <td>O(n*logn)</td> </tr> <tr> <td> <strong>Stable</strong> </td> <td>NO</td> </tr> </table> <ul> <li>The space complexity of quicksort is O(n*logn).</li> </ul> <h2>Implementation of quicksort</h2> <p>Now, let's see the programs of quicksort in different programming languages.</p> <p> <strong>Program:</strong> Write a program to implement quicksort in C language.</p> <pre> #include /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ int partition (int a[], int start, int end) { int pivot = a[end]; // pivot element int i = (start - 1); for (int j = start; j <= 27 end - 1; j++) { if current element is smaller than the pivot (a[j] < pivot) i++; increment index of int t="a[i];" a[i]="a[j];" a[j]="t;" } a[i+1]="a[end];" a[end]="t;" return (i + 1); * function to implement quick sort void quick(int a[], start, end) a[]="array" be sorted, start="Starting" index, (start p="partition(a," end); partitioning quick(a, 1, print an array printarr(int n) i; for i n; i++) printf('%d ', a[i]); main() 24, 9, 29, 14, 19, }; n="sizeof(a)" sizeof(a[0]); printf('before sorting elements are
'); printarr(a, n); 0, printf('
after 0; pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-14.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quick sort in C++ language.</p> <pre> #include using namespace std; /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ int partition (int a[], int start, int end) { int pivot = a[end]; // pivot element int i = (start - 1); for (int j = start; j <= 26 end - 1; j++) { if current element is smaller than the pivot (a[j] < pivot) i++; increment index of int t="a[i];" a[i]="a[j];" a[j]="t;" } a[i+1]="a[end];" a[end]="t;" return (i + 1); * function to implement quick sort void quick(int a[], start, end) a[]="array" be sorted, start="Starting" index, (start p="partition(a," end); partitioning quick(a, 1, print an array printarr(int n) i; for i n; i++) cout< <a[i]<< ' '; main() 23, 8, 28, 13, 18, }; n="sizeof(a)" sizeof(a[0]); cout<<'before sorting elements are
'; printarr(a, n); 0, cout<<'
after 0; pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-15.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quicksort in python.</p> <pre> #function that consider last element as pivot, #place the pivot at its exact position, and place #smaller elements to left of pivot and greater #elements to right of pivot. def partition (a, start, end): i = (start - 1) pivot = a[end] # pivot element for j in range(start, end): # If current element is smaller than or equal to the pivot if (a[j] <= 1 pivot): i="i" + a[i], a[j]="a[j]," a[i] a[i+1], a[end]="a[end]," a[i+1] return (i 1) # function to implement quick sort def quick(a, start, end): a[]="array" be sorted, start="Starting" index, end="Ending" index if (start < p="partition(a," end) is partitioning - 1, printarr(a): print the array for in range(len(a)): (a[i], ) a="[68," 13, 49, 58] print('before sorting elements are ') printarr(a) 0, len(a)-1) print('
after pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-16.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quicksort in Java.</p> <pre> public class Quick { /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ int partition (int a[], int start, int end) { int pivot = a[end]; // pivot element int i = (start - 1); for (int j = start; j <= 25 end - 1; j++) { if current element is smaller than the pivot (a[j] < pivot) i++; increment index of int t="a[i];" a[i]="a[j];" a[j]="t;" } a[i+1]="a[end];" a[end]="t;" return (i + 1); * function to implement quick sort void quick(int a[], start, end) a[]="array" be sorted, start="Starting" index, (start p="partition(a," end); partitioning quick(a, 1, print an array printarr(int n) i; for i n; i++) system.out.print(a[i] ' '); public static main(string[] args) 13, 18, 27, 2, 19, }; n="a.length;" system.out.println('
before sorting elements are q1="new" quick(); q1.printarr(a, n); q1.quick(a, 0, system.out.println('
after system.out.println(); pre> <p> <strong>Output</strong> </p> <p>After the execution of above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-17.webp" alt="Quick Sort Algorithm"> <p> <strong>Program:</strong> Write a program to implement quick sort in php.</p> <pre> <?php /* function that consider last element as pivot, place the pivot at its exact position, and place smaller elements to left of pivot and greater elements to right of pivot. */ function partition (&$a, $start, $end) { $pivot = $a[$end]; // pivot element $i = ($start - 1); for ($j = $start; $j <= $end - 1; $j++) { // If current element is smaller than the pivot if ($a[$j] < $pivot) { $i++; // increment index of smaller element $t = $a[$i]; $a[$i] = $a[$j]; $a[$j] = $t; } } $t = $a[$i+1]; $a[$i+1] = $a[$end]; $a[$end] = $t; return ($i + 1); } /* function to implement quick sort */ function quick(&$a, $start, $end) /* a[] = array to be sorted, start = Starting index, end = Ending index */ { if ($start < $end) { $p = partition($a, $start, $end); //p is partitioning index quick($a, $start, $p - 1); quick($a, $p + 1, $end); } } function printArray($a, $n) { for($i = 0; $i < $n; $i++) { print_r($a[$i]); echo ' '; } } $a = array( 89, 47, 2, 17, 8, 19 ); $n = count($a); echo 'Before sorting array elements are - <br>'; printArray($a, $n); quick($a, 0, $n - 1); echo ' <br> After sorting array elements are - <br>'; printArray($a, $n); ?> </pre> <p> <strong>Output</strong> </p> <p>After the execution of above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/75/quick-sort-algorithm-18.webp" alt="Quick Sort Algorithm"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <p>This article was not only limited to the algorithm. Along with the algorithm, we have also discussed the quick sort complexity, working, and implementation in different programming languages.</p> <hr></=></pre></=></pre></=></pre></=></pre></a[right],></p></a[left],></p></a[right],></p></pivot)></pre></end)> Sortir
Après l'exécution du code ci-dessus, la sortie sera -

Donc, c'est tout à propos de l'article. J'espère que l'article vous sera utile et informatif.
Cet article ne se limitait pas à l’algorithme. Parallèlement à l'algorithme, nous avons également discuté de la complexité, du fonctionnement et de la mise en œuvre du tri rapide dans différents langages de programmation.
latex dérivé partiel
