En mathématiques, partout, il existe une implémentation de ligne. Il est mis en œuvre partout, c'est-à-dire en géométrie, en algèbre et autres. La pente définit la direction de la ligne.
Dans cet article, nous allons aborder deux types de pentes : la pente indéfinie et la pente nulle. Avant de comprendre les types de pente, voyons d'abord la brève description de la pente.
Qu’est-ce que la pente ?
La pente définit le pente de la ligne. Le mot « inclinaison » signifie à quel point la ligne est inclinée. En d’autres termes, la pente montre la direction d’une ligne sur le plan de coordonnées. Ainsi, on l’appelle également le gradient d’une ligne. Les rampes, les escaliers, etc. sont quelques-uns des exemples concrets de pente.
En mathématiques, la pente est le rapport entre « montée » et « course » entre deux points. « Rise » signifie le changement vertical de la ligne et « Run » signifie le changement horizontal de la ligne.
La pente d'une droite entre deux points (x1, et1) et (x2, et2) peut être déterminé en trouvant la différence entre les coordonnées des points. La pente d'une ligne est généralement représentée par la lettre « m ».
m = Δx/Δy = (y2- et1)/(X2- X1)ou, m = monter/courir
Pente indéfinie
La pente indéfinie est la pente de la ligne verticale. Cela signifie que si la ligne est verticale, la pente n'est pas définie. La ligne dans la pente non définie est parallèle à l'axe y et la valeur de ?x est 0. La coordonnée x de la pente non définie ne change jamais, quelle que soit la coordonnée y. Dans une pente indéfinie, la valeur de Δy est un entier non nul, alors que la valeur de Δx est 0. La pente indéfinie est opposée à la pente nulle. En termes de montée et de course, la montée en pente indéfinie est soit positive, soit négative, et la course en pente indéfinie est nulle.
m = Δy/Δx = positif ou négatif Δy/0La valeur indéfinie de m représente la pente indéfinie et la ligne verticale.
Dans le graphique suivant, vous pouvez voir la représentation d'une pente non définie. La ligne dans le graphique ci-dessous est parallèle à l'axe des y qui indique la pente non définie.
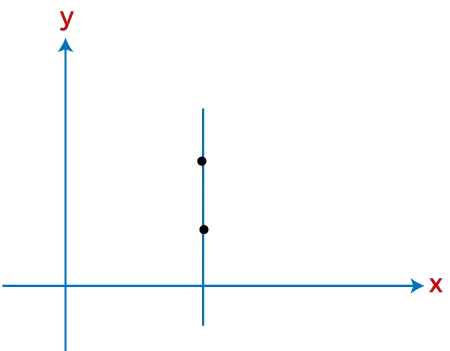
Fig : Représentation d'une pente indéfinie
Dans l'image ci-dessus, il y a une ligne verticale qui indique la pente indéfinie.
Pente nulle
Dans la pente nulle, la ligne est parallèle à l'axe des x et la coordonnée y ne change jamais. C'est la pente de la ligne horizontale. En termes de montée et de course, la montée de la pente nulle est 0 et la course dans la pente nulle est positive.
m = Δy/Δx = 0/Δx positifSi la valeur de m est égale à zéro, la droite est horizontale et a une pente constante.
Dans le graphique suivant, vous pouvez voir la représentation de la pente nulle. La ligne dans le graphique ci-dessous est parallèle à l'axe des x qui indique la pente nulle, et y dans la pente zéro reste le même, quel que soit le x.

Fig : Représentation de la pente nulle
Dans l'image ci-dessus, il y a une ligne horizontale qui indique la pente nulle.
Voyons maintenant la différence entre une pente indéfinie et une pente nulle.
Différence entre pente non définie et pente nulle
La pente indéfinie est opposée à la pente zéro. La différence entre la pente indéfinie et la pente nulle est présentée comme suit :
| Oui Non. | Pente indéfinie | Pente nulle |
|---|---|---|
| 1. | Il est déterminé par la variable X. | Elle est déterminée par la variable Y. |
| 2. | C'est la pente de la ligne verticale. | C'est la pente de la ligne horizontale. |
| 3. | La pente indéfinie n’a aucune valeur concrète, elle a donc une valeur inexistante. | La pente nulle est une valeur déterminée, c'est-à-dire zéro. |
| 4. | Le dénominateur de la pente indéfinie est zéro. | Le numérateur de la pente nulle est zéro. |
| 5. | Dans une pente indéfinie, Y change, mais X ne change pas. | Dans une pente indéfinie, X change, mais Y ne change pas. |
C'est tout à propos de l'article. Nous avons essayé de vous fournir suffisamment d’informations de manière plus simple. J'espère que cela vous sera bénéfique et vous fournira des informations sur la pente non définie, la pente nulle et leur comparaison.
