La formule de pente est utilisée pour déterminer la raideur ou l'inclinaison d'une ligne. Les coordonnées x et y des points situés sur la ligne sont utilisées pour calculer la pente d'une ligne. Le changement de la coordonnée y concernant le changement des coordonnées x est appelé la pente d'une ligne et est généralement représenté par la lettre m.

Table des matières

• Qu'est-ce que la formule de pente ?
• Formule de pente
• Dérivation de la formule de pente
• Formule de pente d'une ligne (ligne droite)
• Équation de pente
• Exemple sur la formule de pente

Qu'est-ce que la formule de pente ?

La formule de pente est nécessaire pour calculer l'inclinaison d'une ligne. Pour calculer la pente d'une ligne, les coordonnées x et y des points sur la ligne sont nécessaires. Le rapport entre le changement des coordonnées y et le changement des coordonnées x est appelé la pente d'une ligne.

Pente (m) = changement de y/changement de x = Δy/Δx

Formule de pente

En mathématiques, la pente d'une ligne est utilisée pour déterminer l'inclinaison de la ligne, c'est-à-dire l'inclinaison d'une ligne. Pour déterminer la pente d’une ligne, nous avons besoin des coordonnées x et y des points situés sur la ligne. La formule de pente est le changement net de la coordonnée y divisé par le changement net de la coordonnée x. Δy est le changement des coordonnées y et Δx est le changement des coordonnées x. Par conséquent, le rapport entre le changement des coordonnées y et le changement des coordonnées x est donné par :

Pente (m) = changement de y/changement de x = Δy/Δx

m = (et ₂ - et ₁ )/(X ₂ - X ₁ )

où

• X₁et x₂sont les coordonnées de l'axe X
• et₁Andy₂sont les coordonnées de l'axe Y

Dérivation de la formule de pente

Les coordonnées x et y de la ligne sont utilisées pour calculer la pente de la ligne. Le changement net de la coordonnée y est Δy, tandis que le changement net de la coordonnée x est Δx. Ainsi, le changement de coordonnée y par rapport au changement de coordonnée x peut s'écrire comme suit :

m = Δy/Δx

où,

• m est la pente
• Δy est le changement des coordonnées y
• Δx est le changement des coordonnées x

On sait que tan θ est aussi la pente de la droite où θ est l'angle que fait la droite avec la direction positive de l'axe des x.

Et, tan θ = hauteur/base

Puisque la hauteur/base entre deux points donnés = (y₂- et₁)/(X₂- X₁)

Ainsi, l’équation de la pente est m = tan θ = Δy/Δx

A partir du graphique, nous observons :

supprimer le cache npm

Δy = (y₂- et₁)

Δx = (x₂- X₁)

La formule de la pente est alors donnée comme suit :

Pente = m = (y ₂ - et ₁ )/(X ₂ - X ₁ )

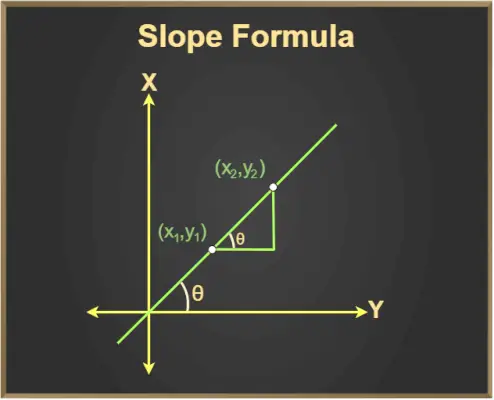
Formule de pente d'une ligne (ligne droite)

• Nous savons que bronzage θ est également une pente de la ligne, donc la pente d'une ligne peut également être représentée comme suit :

Pente (m) = tan θ = Δy/Δx

Où je est l'angle que fait la ligne par rapport à l'axe X positif,

• Δy = changement des coordonnées y,
• Δx = changement des coordonnées x.

• Nous pouvons également définir la pente d'une ligne comme le rapport entre la montée et la course.

Pente (m) = Montée/Courir

• Soit ax + by + c = 0 l'équation générale d'une droite. Maintenant, la formule de la pente de la droite est donnée par :

Pente (m) = – coefficient de x / coefficient de y = -a/b

• La forme à l'origine de la pente d'une droite utilisant l'équation de la droite est donnée par :

y = mx + c

Où m est la pente de la ligne et c est l'ordonnée à l'origine de la ligne.

Équation de pente

La formule de pente est utilisée pour déterminer la pente d'une ligne. L’équation utilisée pour trouver la pente s’écrit :

m = tanθ = Δy/Δx = (y ₂ - et ₁ )/(X ₂ - X ₁ )

où,

• m est la pente de la ligne
• Δy est la différence des coordonnées y
• Δx est la différence entre les coordonnées x
• je est l'angle formé par la ligne avec l'axe des x positif

L'équation de la ligne de pente m est donnée par,

commande chown

y = mx + c

où,

• m est la pente de la ligne
• b est l'ordonnée à l'origine de la ligne

En savoir plus,

• Lignes parallèles
• Forme d'interception de pente

Exemple sur la formule de pente

Exemple 1 : Trouvez la pente d'une droite dont les coordonnées sont (3, 7) et (5, 8).

Solution:

Étant donné, (x₁, et₁) = (3,7) et (x₂, et₂) = (5,8)

Formule de pente (m) = (y ₂ - et ₁ )/(X ₂ - X ₁ )

⇒ m = (8 – 7)/(5 – 3) = 1/2

Par conséquent, la pente de la droite donnée est de 1/2.

arbre de recherche binaire]

Exemple 2 : Déterminer la pente d'une droite dont les coordonnées sont (7, -5) et (2, -3).

Solution:

Étant donné, (x₁, et₁) = (7, -5) et (x₂, et₂) = (23)

Formule de pente (m) = (y ₂ - et ₁ )/(X ₂ - X ₁ )

⇒ m = (-3 – (-5))/(2 – 7) = -2/5

Par conséquent, la pente de la droite donnée est de -2/5

Exemple 3 : Trouver la valeur de a, si la pente d'une droite passant par les points (-4, a) et (2, 5) est 3.

Solution:

Étant donné, (x₁, et₁) = (4,a) et (x₂, et₂) = (2, 5) et pente (m) = 3

java entier en chaîne

On sait que pente (m) = (y ₂ - et ₁ )/(X ₂ - X ₁ )

⇒ 3 = (5 – une)/(2 – 4)

⇒ 3 = (5 – une)/(-2)

⇒ -6 = 5 – une ⇒ une = 5 + 6 = 11

Donc la valeur de a = 11

Exemple 4 : Si une ligne fait un angle de 60° avec l'axe Y positif, alors quelle est la valeur de la pente de la ligne ?

Solution:

Données données, Angle fait par une ligne avec l'axe y positif = 60°

Nous savons que si la ligne fait un angle de 60° par rapport à l’axe y positif, alors elle fait un angle de (90° – 60° = 30°) avec l’axe x.

Donc la valeur de la pente de la droite (m) = tan 30° = 1/√3

Par conséquent, la valeur de la pente de la droite = 1/√3.

Exemple 5 : Sheela vérifiait un graphique et elle a remarqué que la relance était de 12 unités et la course de 4 unités. Calculez maintenant la pente d'une ligne.

Solution:

Étant donné les données, montée = 12 unités et course = 4 unités

On sait que pente (m) = montée/course

⇒ m = 12/4 = 3

Par conséquent, la pente de la droite donnée est de 3

Exemple 6 : Trouvez la pente de la droite 3x – 7y + 8 = 0.

Solution:

Données données, l'équation de la droite = 3x – 7y + 8 = 0

Maintenant, comparez ce qui est donné avec l'équation générale de la droite, c'est-à-dire ax + by + c = 0

Donc a = 3, b = -7 et c = 8

On sait que Pente (m) = – coefficient de x/coefficient de y = -a/b

⇒ m = -3/(-7) = 3/7

Par conséquent, la pente de la droite donnée est de 3/7.

Questions pratiques sur la formule de pente

T1. Calculer la pente d'une droite passant par les points (2, 3) et (5, 7)

Q2. Étant donné l’équation d’une droite : y = 3x – 11, quelle est sa pente ?

Q3. Si la pente d'une droite est de 5/6 et qu'elle passe par le point (2, 5), quelle est l'équation de la droite sous la forme de l'origine de la pente ?

Q4. Calculer la pente d'une droite parallèle aux droites (0, -3) et (1, 11)

Q5. Si la pente d’une droite n’est pas définie, que pouvez-vous conclure à propos de cette droite ?

FAQ sur la formule de pente

Quelle est la pente d’une ligne ?

La pente d'une ligne est la valeur de la raideur ou de l'inclinaison d'une ligne dans le plan x-y. La pente est calculée selon différentes méthodes, selon que l'on donne l'équation de la ligne ou les coordonnées des points sur la ligne.

abc avec des chiffres

Quelle est la formule pour trouver la pente d’une formule tangente ?

La pente d'une ligne est calculée à l'aide de la formule donnée. Supposons que les coordonnées données de deux points situés sur la droite soient (x₁, et₁)/(X_{2 ,}et₂). Alors la formule est donnée par : Pente = m = tan θ = (y ₂ - et ₁ )/(X ₂ - X ₁ )

Quelle est la définition de la formule de pente ?

La formule de pente est définie comme suit :

• Pente = (Changement de la coordonnée y)/(Changement de la coordonnée x)
• Pente = montée/course.

Quelle est la pente d’une formule graphique ?

La pente d'une ligne est la mesure de son inclinaison avec un axe x positif. Mathématiquement, la pente est définie comme s'élever au-dessus de la course .