Dans le monde réel apprentissage automatique Dans les applications, il est courant d’avoir de nombreuses fonctionnalités pertinentes, mais seul un sous-ensemble d’entre elles peut être observable. Lorsqu'il s'agit de variables parfois observables et parfois non, il est en effet possible d'utiliser les instances où cette variable est visible ou observée afin d'apprendre et de faire des prédictions pour les instances où elle n'est pas observable. Cette approche est souvent appelée gestion des données manquantes. En utilisant les instances disponibles où la variable est observable, les algorithmes d'apprentissage automatique peuvent apprendre des modèles et des relations à partir des données observées. Ces modèles appris peuvent ensuite être utilisés pour prédire les valeurs de la variable dans les cas où elle est manquante ou non observable.
L'algorithme d'espérance-maximisation peut être utilisé pour gérer des situations où les variables sont partiellement observables. Lorsque certaines variables sont observables, nous pouvons utiliser ces instances pour apprendre et estimer leurs valeurs. Ensuite, nous pouvons prédire les valeurs de ces variables dans les cas où elles ne sont pas observables.
L'algorithme EM a été proposé et nommé dans un article fondateur publié en 1977 par Arthur Dempster, Nan Laird et Donald Rubin. Leurs travaux ont formalisé l'algorithme et démontré son utilité dans la modélisation et l'estimation statistiques.
L'algorithme EM est applicable aux variables latentes, qui sont des variables qui ne sont pas directement observables mais qui sont déduites des valeurs d'autres variables observées. En exploitant la forme générale connue de la distribution de probabilité régissant ces variables latentes, l'algorithme EM peut prédire leurs valeurs.
L'algorithme EM sert de base à de nombreux algorithmes de clustering non supervisés dans le domaine de l'apprentissage automatique. Il fournit un cadre pour trouver les paramètres locaux du maximum de vraisemblance d'un modèle statistique et déduire des variables latentes dans les cas où les données sont manquantes ou incomplètes.
Algorithme d’attente-maximisation (EM)
L'algorithme d'espérance-maximisation (EM) est une méthode d'optimisation itérative qui combine différentes méthodes non supervisées. apprentissage automatique algorithmes pour trouver le maximum de vraisemblance ou des estimations a posteriori maximales de paramètres dans des modèles statistiques qui impliquent des variables latentes non observées. L'algorithme EM est couramment utilisé pour les modèles à variables latentes et peut gérer les données manquantes. Il consiste en une étape d'estimation (étape E) et une étape de maximisation (étape M), formant un processus itératif pour améliorer l'ajustement du modèle.
- À l'étape E, l'algorithme calcule les variables latentes, c'est-à-dire l'attente de la log-vraisemblance en utilisant les estimations des paramètres actuels.
- À l'étape M, l'algorithme détermine les paramètres qui maximisent la log-vraisemblance attendue obtenue à l'étape E, et les paramètres du modèle correspondants sont mis à jour sur la base des variables latentes estimées.

Attente-Maximisation dans l'algorithme EM
En répétant ces étapes de manière itérative, l'algorithme EM cherche à maximiser la probabilité des données observées. Il est couramment utilisé pour des tâches d'apprentissage non supervisées, telles que le clustering, où des variables latentes sont déduites et a des applications dans divers domaines, notamment l'apprentissage automatique, la vision par ordinateur et le traitement du langage naturel.
acteur Govinda
Termes clés de l’algorithme d’attente-maximisation (EM)
Certains des termes clés les plus couramment utilisés dans l’algorithme d’attente-maximisation (EM) sont les suivants :
- Variables latentes : les variables latentes sont des variables non observées dans les modèles statistiques qui ne peuvent être déduites qu'indirectement par leurs effets sur les variables observables. Ils ne peuvent pas être mesurés directement mais peuvent être détectés par leur impact sur les variables observables. Probabilité : C'est la probabilité d'observer les données données compte tenu des paramètres du modèle. Dans l’algorithme EM, l’objectif est de trouver les paramètres qui maximisent la vraisemblance. Log-vraisemblance : il s'agit du logarithme de la fonction de vraisemblance, qui mesure la qualité de l'ajustement entre les données observées et le modèle. L'algorithme EM cherche à maximiser la log-vraisemblance. Estimation du maximum de vraisemblance (MLE) : MLE est une méthode permettant d'estimer les paramètres d'un modèle statistique en trouvant les valeurs des paramètres qui maximisent la fonction de vraisemblance, qui mesure dans quelle mesure le modèle explique les données observées. Probabilité postérieure : dans le contexte de l'inférence bayésienne, l'algorithme EM peut être étendu pour estimer les estimations maximales a posteriori (MAP), où la probabilité postérieure des paramètres est calculée sur la base de la distribution a priori et de la fonction de vraisemblance. Étape d'attente (E) : L'étape E de l'algorithme EM calcule la valeur attendue ou la probabilité postérieure des variables latentes en fonction des données observées et des estimations des paramètres actuels. Cela implique de calculer les probabilités de chaque variable latente pour chaque point de données. Étape de maximisation (M) : L'étape M de l'algorithme EM met à jour les estimations des paramètres en maximisant la log-vraisemblance attendue obtenue à partir de l'étape E. Il s’agit de trouver les valeurs des paramètres qui optimisent la fonction de vraisemblance, généralement grâce à des méthodes d’optimisation numérique. Convergence : La convergence fait référence à la condition dans laquelle l'algorithme EM a atteint une solution stable. Il est généralement déterminé en vérifiant si la modification de la log-vraisemblance ou des estimations des paramètres tombe en dessous d'un seuil prédéfini.
Comment fonctionne l'algorithme d'attente-maximisation (EM) :
L'essence de l'algorithme d'espérance-maximisation est d'utiliser les données observées disponibles de l'ensemble de données pour estimer les données manquantes, puis d'utiliser ces données pour mettre à jour les valeurs des paramètres. Comprenons l'algorithme EM en détail.

Organigramme de l'algorithme EM
- Initialisation :
- Dans un premier temps, un ensemble de valeurs initiales des paramètres est considéré. Un ensemble de données observées incomplètes est fourni au système en supposant que les données observées proviennent d'un modèle spécifique.
- Calculez la probabilité ou la responsabilité a posteriori de chaque variable latente en fonction des données observées et des estimations des paramètres actuels.
- Estimez les valeurs des données manquantes ou incomplètes à l’aide des estimations de paramètres actuelles.
- Calculez le log de vraisemblance des données observées sur la base des estimations des paramètres actuels et des données manquantes estimées.
- Mettez à jour les paramètres du modèle en maximisant la vraisemblance complète attendue du journal des données obtenue à partir de l’étape E.
- Cela implique généralement de résoudre des problèmes d'optimisation pour trouver les valeurs de paramètres qui maximisent la log-vraisemblance.
- La technique d'optimisation spécifique utilisée dépend de la nature du problème et du modèle utilisé.
- Vérifiez la convergence en comparant le changement de log-vraisemblance ou les valeurs des paramètres entre les itérations.
- Si le changement est inférieur à un seuil prédéfini, arrêtez-vous et considérez l'algorithme convergé.
- Sinon, revenez à l'étape E et répétez le processus jusqu'à ce que la convergence soit atteinte.
Mise en œuvre étape par étape de l'algorithme d'attente-maximisation
Importez les bibliothèques nécessaires
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
chaîne dans un tableau java
>
>
Générer un ensemble de données avec deux composantes gaussiennes
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
pandas créant un dataframe
>
Sortir :

Tracé de densité
Initialiser les paramètres
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Effectuer l'algorithme EM
- Itère pendant le nombre d'époques spécifié (20 dans ce cas).
- À chaque époque, l'étape E calcule les responsabilités (valeurs gamma) en évaluant les densités de probabilité gaussiennes pour chaque composante et en les pondérant par les proportions correspondantes.
- L'étape M met à jour les paramètres en calculant la moyenne pondérée et l'écart type pour chaque composant
Python3
suppression d'un arbre de recherche binaire
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Sortir :

Époque vs log-vraisemblance
Tracez la densité finale estimée
Python3
lecture de fichier csv en java
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Sortir :
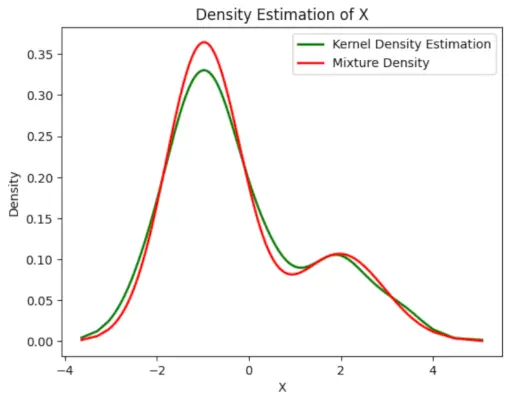
Densité estimée
Applications du Algorithme EM
- Il peut être utilisé pour compléter les données manquantes dans un échantillon.
- Il peut être utilisé comme base d’apprentissage non supervisé de clusters.
- Il peut être utilisé dans le but d’estimer les paramètres du modèle de Markov caché (HMM).
- Il peut être utilisé pour découvrir les valeurs des variables latentes.
Avantages de l'algorithme EM
- Il est toujours garanti que la probabilité augmentera à chaque itération.
- Les étapes E et M sont souvent assez simples pour résoudre de nombreux problèmes en termes de mise en œuvre.
- Les solutions aux étapes M existent souvent sous forme fermée.
Inconvénients de l'algorithme EM
- Sa convergence est lente.
- Il fait convergence vers les optimums locaux uniquement.
- Cela nécessite à la fois les probabilités, avant et arrière (l'optimisation numérique ne nécessite que la probabilité avant).
