La fonction Supprimer est utilisée pour supprimer le nœud spécifié d’un arbre de recherche binaire. Cependant, nous devons supprimer un nœud d'un arbre de recherche binaire de telle manière que la propriété de l'arbre de recherche binaire ne soit pas violée. Il existe trois situations de suppression d'un nœud de l'arbre de recherche binaire.
Le nœud à supprimer est un nœud feuille
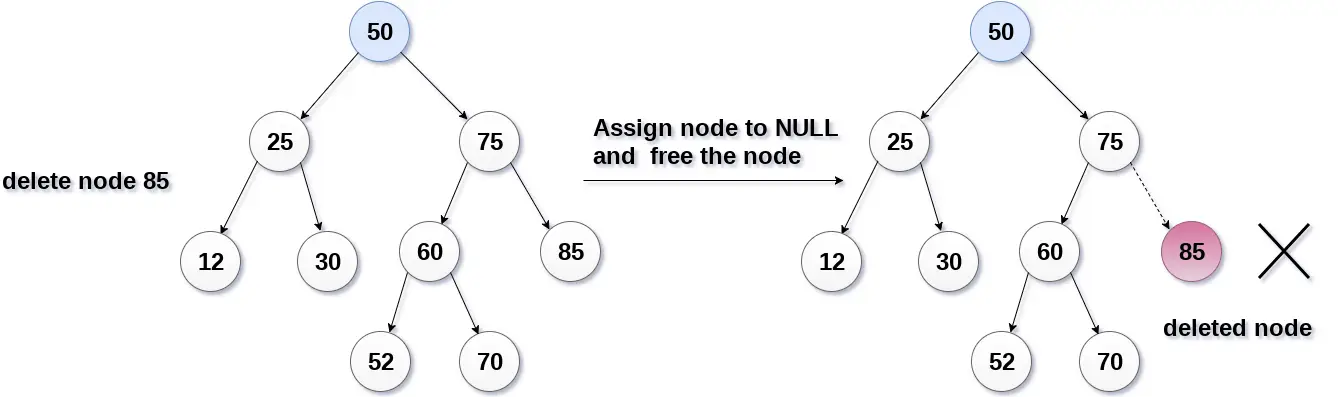
C'est le cas le plus simple, dans ce cas, remplacez le nœud feuille par le NULL et libérez simplement l'espace alloué.
Dans l'image suivante, nous supprimons le nœud 85, puisque le nœud est un nœud feuille, donc le nœud sera remplacé par NULL et l'espace alloué sera libéré.
Le nœud à supprimer n'a qu'un seul enfant.
Dans ce cas, remplacez le nœud par son enfant et supprimez le nœud enfant, qui contient désormais la valeur à supprimer. Remplacez-le simplement par le NULL et libérez l'espace alloué.
Dans l'image suivante, le nœud 12 est à supprimer. Il n'a qu'un seul enfant. Le nœud sera remplacé par son nœud enfant et le nœud remplacé 12 (qui est maintenant le nœud feuille) sera simplement supprimé.

Le nœud à supprimer a deux enfants.
C'est un cas un peu complexe comparé aux deux autres cas. Cependant, le nœud qui doit être supprimé est remplacé par son successeur ou prédécesseur dans l'ordre de manière récursive jusqu'à ce que la valeur du nœud (à supprimer) soit placée sur la feuille de l'arborescence. Après la procédure, remplacez le nœud par NULL et libérez l'espace alloué.
Dans l'image suivante, le nœud 50 est à supprimer qui est le nœud racine de l'arborescence. Le parcours dans l’ordre de l’arbre donné ci-dessous.
6, 25, 30, 50, 52, 60, 70, 75.
remplacez 50 par son successeur dans l'ordre 52. Désormais, 50 sera déplacé vers la feuille de l'arborescence, qui sera simplement supprimée.

Algorithme
Supprimer (ARBRE, ARTICLE)
Écrivez « élément introuvable dans l'arborescence » SINON SI DONNÉES SUR L'ÉLÉMENT
Supprimer(ARBRE->GAUCHE, ARTICLE)
AUTRE SI ARTICLE > ARBRE -> DONNÉES
Supprimer (ARBRE -> DROITE, ARTICLE)
AUTRE SI ARBRE -> GAUCHE ET ARBRE -> DROITE
SET TEMP = findLargestNode (ARBRE -> GAUCHE)
DÉFINIR L'ARBRE -> DONNÉES = TEMP -> DONNÉES
Supprimer (ARBRE -> GAUCHE, TEMP -> DONNÉES)
AUTRE
RÉGLER TEMP = ARBRE
SI ARBRE -> GAUCHE = NULL ET ARBRE -> DROITE = NULL
FIXER L'ARBRE = NULL
AUTRE SI ARBRE -> GAUCHE != NULL
DÉFINIR ARBRE = ARBRE -> GAUCHE
AUTRE
DÉFINIR ARBRE = ARBRE -> DROITE
[FIN DE SI]
TEMPÉRATURE LIBRE
[FIN DE SI]
Fonction:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 