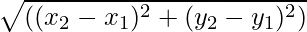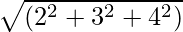logo

TechCodeview

Magnitude d'un vecteur

Les quantités vectorielles sont les quantités qui ont à la fois une direction et une ampleur. La norme d'un vecteur est la longueur du vecteur. Il est donné par la valeur numérique du vecteur et comme il représente la longueur du vecteur, il est toujours positif. Pour n'importe quel vecteur 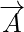overrightarrow{A}sa grandeur est représentée par overrightarrow{A}.

Apprenons-en davantage sur l'ampleur du vecteur, sa formule, des exemples et autres dans cet article.



Table des matières

Quelle est la grandeur d'un vecteur ?

La grandeur d'un vecteur est définie comme la longueur du vecteur. Comme la norme du vecteur indique la longueur du vecteur, elle est toujours positive. Pour tout vecteur A, sa norme est représentée par |A|. Supposons qu'un vecteur soit défini comme xi + yj, alors sa norme est définie comme la racine carrée de la somme des carrés des termes individuels. L'ampleur du vecteur représente la longueur du vecteur, c'est-à-dire la valeur ou l'impact du vecteur.

Par exemple, si une force de 5i N agit sur un objet, alors sa magnitude est de 5 N, ce qui signifie que la force de la force appliquée est de 5 N, et « je' en 5i représente qu'il est appliqué dans la direction x positive.



Ampleur d'une formule vectorielle

Il existe différentes manières de calculer la norme du vecteur. Sur la base des données fournies, utilisez un autre type de formule pour trouver la norme d'un vecteur. La norme d'un vecteur A est représentée à l'aide de l'opérateur de module, c'est-à-dire |A|

Il existe différentes formules utilisées pour compter la magnitude du vecteur. L'image suivante montre les formules importantes utilisées pour trouver la norme du vecteur.

Ampleur d'une formule vectorielle

Voici les façons de calculer la magnitude.



  • Si on leur donne un vecteur Ā = xi+ yĵ + zk̂ alors la grandeur du vecteur Ā peut être calculée à l'aide de la formule ci-dessous

Amplitude du vecteur  (|A|) = √(x 2 + et 2 +z 2 )

  • Si le vecteur de point de départ est disons (x1, et1) et le point final d'un vecteur est disons (x2, et2) sont alors données la norme du vecteur overrightarrow{AB}est donné par,
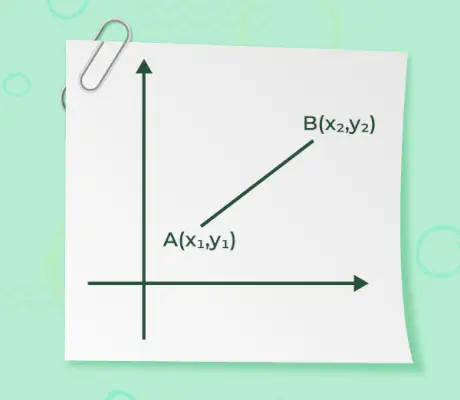
Magnitude du vecteur si deux points sont donnés

La grandeur d'un vecteur, lorsque les points de départ et d'arrivée d'un vecteur sont donnés, n'est rien d'autre que la distance entre les points. La formule pour trouver la grandeur est donnée par

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Si l’un des points de départ ou d’arrivée d’un vecteur est à l’origine o(0, 0) et qu’un autre point est UNE(x,y) comme spécifié dans la figure ci-dessous,
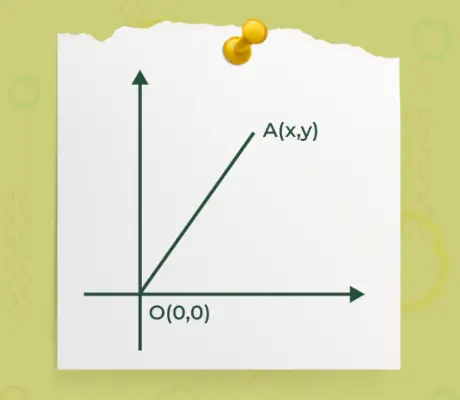
Magnitude du vecteur si un point et une origine sont donnés

Ensuite, la formule pour trouver la norme d'un vecteur dont l'une des extrémités d'un vecteur est à l'origine est donnée par

|À| = √(x 2 +o 2 )

Direction d'un vecteur

Les quantités vectorielles sont des quantités qui ont à la fois des grandeurs et des directions. La direction de la quantité vectorielle indique dans quelle direction la quantité vectorielle est appliquée. Il est défini comme l'angle que fait le vecteur avec la ligne horizontale ou l'axe des x. Il est représenté par le symbole un .

L'image ci-dessous montre la flèche utilisée pour indiquer la direction du vecteur.

Direction du vecteur

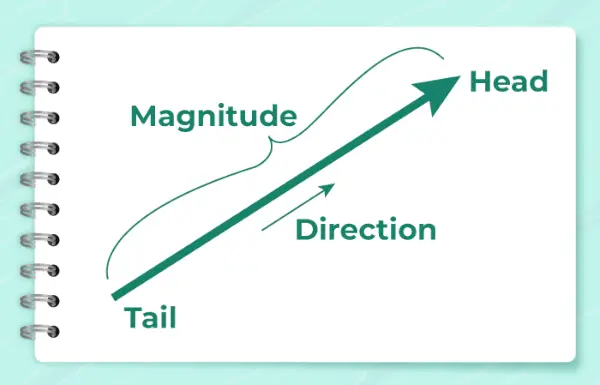
Il est calculé à l'aide de la formule,

α = bronzage -1 (o/x)

exemple java bonjour le monde

Pour le vecteur généré par les coordonnées (x1, et1) et (x2, et2) leur direction est donnée par la formule,

α = bronzage -1 [(et 2 - et 1 )/(X 2 - X 1 )]

Comment trouver la grandeur d’un vecteur ?

L'amplitude du vecteur est calculée en utilisant les étapes décrites ci-dessous,

Étape 1: Identifiez les composantes x, y et z du vecteur.

Étape 2 : Trouvez le carré de toutes les composantes x, y et z.

Étape 3: Ajoutez tous les carrés trouvés à l'étape 2.

Étape 4: Trouvez la racine carrée de la somme obtenue à l'étape 3.

La valeur obtenue après l'étape 4 est la norme du vecteur donné.

Exemple : Trouver la norme du vecteur A = 3i + 4j

Solution:

L'amplitude du vecteur A est calculée en utilisant les étapes décrites ci-dessus.

entier pour doubler Java

Étape 1: En comparant A = 3i + 4j avec xi + yj, nous obtenons x = 3 et y = 4

Étape 2: X2= 32= 9 et y2= 42= 16

Étape 3: X2+ et2= 9 + 16 = 25

Étape 4: √(25) = 5

Ainsi, la norme du vecteur A = 3i + 4j est de 5 unités.

Conclusion

En conclusion, la norme d’un vecteur nous indique sa longueur. Ce concept est très important dans de nombreux domaines comme la physique, l’ingénierie et l’informatique, car il permet de mesurer des éléments tels que la vitesse, la force et la direction du mouvement. En comprenant la magnitude vectorielle, nous pouvons mieux analyser et résoudre des problèmes pratiques, ce qui en fait un élément de connaissance clé pour quiconque travaille avec des nombres et des mesures dans des applications du monde réel.

En savoir plus,

Exemples résolus sur la grandeur du vecteur

Exemple 1 : Trouvez la norme du vecteur Ā = 2i + 3ĵ + 4k.

Solution:

fusion de pd

Donné,

Ā = 2i + 3ĵ + 4k

Magnitude |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

L'ampleur du vecteur 2i+3ĵ+4k est 5.38 unité

Exemple 2 : Trouver la norme du vecteur Ā = 3i + 3ĵ – 6k

Solution:

Donné

 = 3i + 3ĵ – 6k

Magnitude |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

L'ampleur du vecteur 3i+ 3ĵ – 6k est 7h35 unité.

Exemple 3 : Trouvez la norme du vecteur si le point de départ d'un vecteur est (3, 4) et le point final est (6, 2).

Solution:

Donné,

(X1, et1) = (3, 4)
(X2, et2) = (6, 2)

raccourci tout en majuscules excel

|À|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Ainsi, la norme du vecteur donné est 3.6 unité.

Exemple 4 : Trouvez la norme du vecteur si le point de départ d'un vecteur est (2, 1, 4) et le point final est (5, 2, 6).

Solution:

Donné,

(X1, et1, Avec1) = (2, 1, 4)

(X2, et2, Avec2) = (5, 2, 6)

|À| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Ainsi, la norme du vecteur donné est 3,74 unité.

Exemple 5 : Quelle est la norme du vecteur qui commence à l'origine et au point final en (3, 4).

Solution:

Donné,

Le point de départ du vecteur est O (0, 0)

Point final (x, y) = (3, 4)

Amplitude du vecteur (|Ā|) = √(x2+o2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Ainsi, la norme du vecteur donné est 5 unité.

Exemple 6 : Trouver la norme du vecteur dans lequel l'une des extrémités est à l'origine et l'autre point à (1, 4, 3).

Solution:

Donné,

Le point final du vecteur est O (0, 0)

Autre point (x, y, z) = (1, 4, 3)

Amplitude du vecteur (|Ā|) = √(x2+o2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Ainsi, la norme du vecteur donné est 5.09 unité.

Acteur Ekta Kapoor

FAQ sur la grandeur d'un vecteur

Quelle est la grandeur d’une formule vectorielle ?

La magnitude d'un vecteur est la valeur numérique du vecteur et définit la longueur du vecteur. Pour tout vecteur A, sa norme est représentée par |A|. L'amplitude du vecteur est calculée à l'aide de la formule,

Pour tout vecteur A = xi + yj + zk, sa norme est donnée par la formule

|UNE| = √(x 2 + et 2 + z 2 )

Pour tout vecteur dont le point de départ et le point final sont respectivement (x1, et1) et (x2, et2) sa grandeur est donnée par la formule

|UNE| = √((x 2 - X 1 ) 2 + (et 2 - et 1 ) 2 )

Comment représenter la grandeur d'un vecteur ?

L'ampleur du vecteur UN est représenté par le symbole |A|.

Comment trouver la grandeur d'un vecteur ?

Diverses formules sont utilisées pour calculer la magnitude du vecteur, certaines d'entre elles sont,

  • |UNE| = √(x 2 + et 2 + z 2 ) lorsque le vecteur est sous la forme A = xi + yj + zk
  • |UNE| = √((x) 2 + (et) 2 ) lorsque le vecteur est donné par le point A (x, y) et l'origine O(0, 0).
  • |UNE| = √((x 2 - X 1 ) 2 + (et 2 - et 1 ) 2 ) lorsque le vecteur est donné par le point A (x1, et2) et le point B (x2, et2).

Trouvez un vecteur de magnitude 5.

Il existe différents vecteurs qui peuvent avoir une magnitude de 5, dont un exemple est le vecteur A représenté par :

A = 3i + 4j Ou A = 4i + 5j