Divide and Conquer est un modèle algorithmique. Dans les méthodes algorithmiques, la conception consiste à prendre un différend sur une entrée énorme, à diviser l'entrée en éléments mineurs, à résoudre le problème sur chacun des petits éléments, puis à fusionner les solutions par morceaux en une solution globale. Ce mécanisme de résolution du problème est appelé la stratégie Divide & Conquer.

L’algorithme Divide and Conquer consiste en une dispute utilisant les trois étapes suivantes.

Diviserle problème initial en un ensemble de sous-problèmes.Conquérir:Résolvez chaque sous-problème individuellement, de manière récursive.Combiner:Rassemblez les solutions des sous-problèmes pour obtenir la solution à l’ensemble du problème.

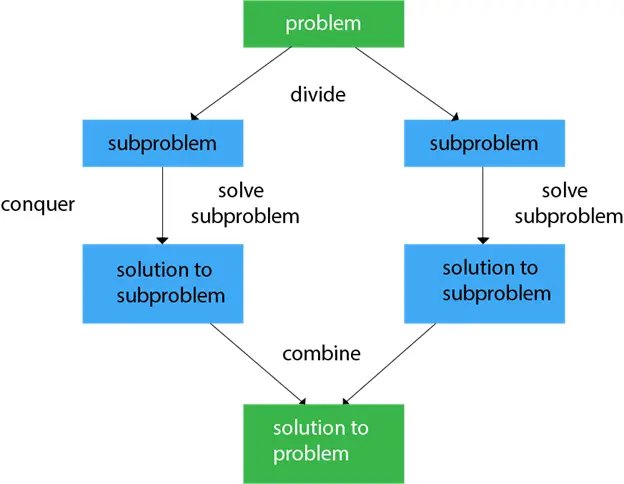
En général, nous pouvons suivre le diviser et conquérir approche en trois étapes.

Exemples: Les algorithmes informatiques spécifiques sont basés sur l’approche Divide & Conquer :

1. Problème maximum et minimum
2. Recherche binaire
3. Tri (tri par fusion, tri rapide)
4. La tour de Hanoi.

Fondamentaux de la stratégie Divide & Conquer :

Il y a deux principes fondamentaux dans la stratégie Divide & Conquer :

1. Formule relationnelle
2. Condition d'arrêt

1. Formule relationnelle : C'est la formule que nous générons à partir de la technique donnée. Après la génération de la formule, nous appliquons la stratégie D&C, c'est-à-dire que nous résolvons le problème de manière récursive et résolvons les sous-problèmes résolus.

2. Conditions d'arrêt : Lorsque nous résolvons le problème en utilisant la stratégie Divide & Conquer, nous devons alors savoir que pendant combien de temps nous devons appliquer Divide & Conquer. Ainsi, la condition dans laquelle il est nécessaire d'arrêter nos étapes de récursion de D&C est appelée condition d'arrêt.

Applications de l’approche Diviser pour régner :

Les algorithmes suivants sont basés sur le concept de la technique Divide and Conquer :

Recherche binaire:L'algorithme de recherche binaire est un algorithme de recherche, également appelé recherche à demi-intervalle ou recherche logarithmique. Cela fonctionne en comparant la valeur cible avec l'élément du milieu existant dans un tableau trié. Après avoir effectué la comparaison, si la valeur diffère, la moitié qui ne peut pas contenir la cible sera finalement éliminée, puis la recherche se poursuivra sur l'autre moitié. Nous allons à nouveau considérer l'élément intermédiaire et le comparer avec la valeur cible. Le processus continue de se répéter jusqu'à ce que la valeur cible soit atteinte. Si nous trouvons l’autre moitié vide après avoir terminé la recherche, nous pouvons alors conclure que la cible n’est pas présente dans le tableau.Tri rapide:Il s'agit de l'algorithme de tri le plus efficace, également connu sous le nom de tri par échange de partitions. Cela commence par sélectionner une valeur pivot dans un tableau, puis diviser le reste des éléments du tableau en deux sous-tableaux. La partition est réalisée en comparant chacun des éléments avec la valeur pivot. Il compare si l'élément contient une valeur supérieure ou inférieure à celle du pivot, puis trie les tableaux de manière récursive.Tri par fusion:C'est un algorithme de tri qui trie un tableau en effectuant des comparaisons. Cela commence par diviser un tableau en sous-tableaux, puis trie récursivement chacun d'eux. Une fois le tri effectué, il les fusionne.Paire de points la plus proche :C'est un problème de géométrie computationnelle. Cet algorithme met l'accent sur la recherche de la paire de points la plus proche dans un espace métrique, étant donné n points, de telle sorte que la distance entre la paire de points soit minimale.L'algorithme de Strassen :Il s'agit d'un algorithme de multiplication matricielle, qui porte le nom de Volker Strassen. Il s’est avéré beaucoup plus rapide que l’algorithme traditionnel lorsqu’il travaille sur de grandes matrices.Algorithme de transformée de Fourier rapide (FFT) de Cooley-Tukey :L'algorithme de transformée de Fourier rapide porte le nom de J. W. Cooley et John Turkey. Il suit l’approche Divide and Conquer et impose une complexité de O(nlogn).Algorithme Karatsuba pour une multiplication rapide :Il s'agit de l'un des algorithmes de multiplication les plus rapides de l'époque traditionnelle, inventé par Anatoly Karatsuba à la fin des années 1960 et publié en 1962. Il multiplie deux nombres à n chiffres de telle manière en les réduisant à un seul chiffre au maximum.

Avantages de diviser pour régner

• Divide and Conquer a tendance à résoudre avec succès l'un des plus gros problèmes, comme la Tour de Hanoï, un casse-tête mathématique. Il est difficile de résoudre des problèmes compliqués pour lesquels vous n'avez aucune idée de base, mais avec l'aide de l'approche diviser pour régner, l'effort a été réduit car il s'agit de diviser le problème principal en deux moitiés, puis de les résoudre de manière récursive. Cet algorithme est beaucoup plus rapide que les autres algorithmes.
• Il utilise efficacement la mémoire cache sans occuper beaucoup d'espace, car il résout de simples sous-problèmes au sein de la mémoire cache au lieu d'accéder à la mémoire principale, plus lente.
• Il est plus efficace que celui de son homologue, la technique Brute Force.
• Ces algorithmes inhibant le parallélisme, celui-ci n’implique aucune modification et est géré par des systèmes intégrant un traitement parallèle.

Inconvénients de diviser pour régner

• Étant donné que la plupart de ses algorithmes sont conçus en incorporant la récursion, cela nécessite une gestion élevée de la mémoire.
• Une pile explicite peut abuser de l'espace.
• Cela peut même faire planter le système si la récursivité est effectuée avec une rigueur supérieure à celle de la pile présente dans le CPU.