Avant de comprendre Arbre B et Arbre B+ différences, nous devrions connaître l’arbre B et l’arbre B+ séparément.
Qu'est-ce que l'arbre B ?
Arbre B est un arbre auto-équilibré, et c'est un arbre m-way où m définit l'ordre de l'arbre. Arbre B est une généralisation de Arbre de recherche binaire dans lequel un nœud peut avoir plus d'une clé et plus de deux enfants en fonction de la valeur de m . Dans l'arbre B, les données sont spécifiées dans un ordre trié ayant des valeurs inférieures dans le sous-arbre de gauche et des valeurs plus élevées dans le sous-arbre de droite.
javatable
Propriétés de l'arbre B
Voici les propriétés de l’arbre B :
- Dans l'arbre B, tous les nœuds feuilles doivent être au même niveau, alors que, dans le cas d'un arbre binaire, les nœuds feuilles peuvent être à des niveaux différents.
Comprenons cette propriété à travers un exemple.
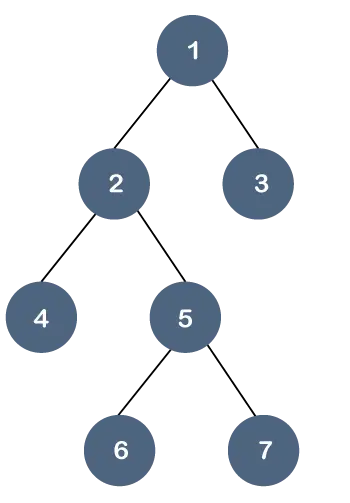
Dans l’arborescence ci-dessus, tous les nœuds feuilles ne sont pas au même niveau, mais ils ont au maximum deux enfants. On peut donc dire que l’arbre ci-dessus est un arbre binaire mais pas un arbre B.
- Si le Btree a un ordre de m, alors chaque nœud peut avoir un maximum de m Dans le cas d'enfants minimum, les nœuds feuilles ont zéro enfant, le nœud racine a deux enfants et les nœuds internes ont un plafond de m/2.
- Chaque nœud peut avoir un maximum de (m-1) clés. Par exemple, si la valeur de m est 5, alors la valeur maximale des clés est 4.
- Le nœud racine a au minimum une clé, alors que tous les autres nœuds à l'exception du nœud racine ont (plafond de m/2 moins - 1) un minimum de clés.
- Si nous effectuons une insertion dans l’arbre B, alors le nœud est toujours inséré dans le nœud feuille.
Supposons que nous voulions créer un arbre B d'ordre 3 en insérant des valeurs de 1 à 10.
Étape 1: Tout d’abord, nous créons un nœud avec 1 valeur comme indiqué ci-dessous :

Étape 2: L'élément suivant est 2, qui vient après 1 comme indiqué ci-dessous :

Étape 3: L'élément suivant est 3, et il est inséré après 2 comme indiqué ci-dessous :

Comme nous savons que chaque nœud peut avoir 2 clés maximum, nous allons donc diviser ce nœud par l'élément du milieu. L'élément du milieu est 2, il se déplace donc vers son parent. Le nœud 2 n'a pas de parent, il deviendra donc le nœud racine comme indiqué ci-dessous :

Étape 4: L'élément suivant est 4. Puisque 4 est supérieur à 2 et 3, il sera donc ajouté après le 3 comme indiqué ci-dessous :

Étape 5 : L'élément suivant est 5. Puisque 5 est supérieur à 2, 3 et 4, il sera donc ajouté après 4 comme indiqué ci-dessous :

Comme nous savons que chaque nœud peut avoir 2 clés maximum, nous allons donc diviser ce nœud par l'élément du milieu. L'élément du milieu est 4, donc il se déplace vers son parent. Le parent est le nœud 2 ; par conséquent, 4 sera ajouté après 2 comme indiqué ci-dessous :

Étape 6 : L'élément suivant est 6. Puisque 6 est supérieur à 2, 4 et 5, donc 6 viendra après 5 comme indiqué ci-dessous :

Étape 7 : L'élément suivant est 7. Puisque 7 est supérieur à 2, 4, 5 et 6, donc 7 viendra après 6 comme indiqué ci-dessous :

Comme nous savons que chaque nœud peut avoir 2 clés maximum, nous allons donc diviser ce nœud par l'élément du milieu. L'élément du milieu est 6, il se déplace donc vers son parent comme indiqué ci-dessous :

Mais 6 ne peut pas être ajouté après 4 car le nœud peut avoir 2 clés maximum, nous allons donc diviser ce nœud par l'élément du milieu. L'élément du milieu est 4, il se déplace donc vers son parent. Comme le nœud 4 n'a aucun parent, le nœud 4 deviendra un nœud racine comme indiqué ci-dessous :

Qu'est-ce qu'un arbre B+ ?
Le Arbre B+ est également connu comme un arbre auto-équilibré avancé car chaque chemin depuis la racine de l'arbre jusqu'à la feuille de l'arbre a la même longueur. Ici, la même longueur signifie que tous les nœuds feuilles se trouvent au même niveau. Il n’arrivera pas que certains nœuds feuilles se produisent au troisième niveau et d’autres au deuxième niveau.
Un index arborescent B+ est considéré comme un index multi-niveaux, mais la structure arborescente B+ n'est pas similaire aux fichiers séquentiels d'index multi-niveaux.
Pourquoi l’arbre B+ est-il utilisé ?
Un arbre B+ est utilisé pour stocker les enregistrements de manière très efficace en stockant les enregistrements de manière indexée à l'aide de la structure indexée de l'arbre B+. Grâce à l'indexation à plusieurs niveaux, l'accès aux données devient plus rapide et plus facile.
Structure des nœuds de l'arbre B+
La structure des nœuds de l'arborescence B+ contient des pointeurs et des valeurs clés illustrées dans la figure ci-dessous :

Comme nous pouvons l’observer dans la structure de nœud de l’arbre B+ ci-dessus, elle contient n-1 valeurs clés (k1à kn-1) et n pointeurs (p1hautn).
Les valeurs de clé de recherche placées dans le nœud sont conservées dans un ordre trié. Ainsi, si je
Contrainte sur différents types de nœuds
Soit 'b' l'ordre de l'arbre B+.
Nœud non-feuille
Bourne encore une coquille
Soit 'm' représentant le nombre d'enfants d'un nœud, alors la relation entre l'ordre de l'arbre et le nombre d'enfants peut être représentée comme :

Soit k représente les valeurs des clés de recherche. La relation entre l’ordre de l’arborescence et la clé de recherche peut être représentée comme suit :
Comme nous savons que le nombre de pointeurs est égal aux valeurs des clés de recherche plus 1, donc mathématiquement, cela peut s'écrire comme suit :
Nombre de pointeurs (ou enfants) = Nombre de clés de recherche + 1
Par conséquent, le nombre maximum de pointeurs serait « b », et le nombre minimum de pointeurs serait la fonction plafond de b/2.
Noeud feuille
Un nœud feuille est un nœud qui se produit au dernier niveau de l'arborescence B+, et chaque nœud feuille utilise un seul pointeur pour se connecter les uns aux autres afin de fournir un accès séquentiel au niveau feuille.
Dans le nœud feuille, le nombre maximum d'enfants est :

Le nombre maximum de clés de recherche est :

Noeud principal
Le nombre maximum d'enfants dans le cas du nœud racine est : b
Le nombre minimum d'enfants est de : 2
Cas particuliers dans l'arbre B+
Cas 1: Si le nœud racine est le seul nœud de l'arborescence. Dans ce cas, le nœud racine devient le nœud feuille.
Dans ce cas, le nombre maximum d'enfants est 1, c'est-à-dire le nœud racine lui-même, tandis que le nombre minimum d'enfants est b-1, ce qui est le même que celui d'un nœud feuille.
Représentation d'un nœud feuille dans un arbre B+

Dans la figure ci-dessus, '.' représente le pointeur, tandis que les 10, 20 et 30 sont les valeurs clés. Le pointeur contient l'adresse à laquelle la valeur clé est stockée, comme le montre la figure ci-dessus.
Exemple d'arbre B+

Dans la figure ci-dessus, le nœud contient trois valeurs clés, à savoir 9, 16 et 25. Le pointeur qui apparaît avant 9 contient les valeurs clés inférieures à 9 représentées par kje. Le pointeur qui apparaît avant 16 contient les valeurs clés supérieures ou égales à 9 mais inférieures à 16 représentées par kj. Le pointeur qui apparaît avant 25, contient les valeurs clés supérieures ou égales à 16 mais inférieures à 25 représentées par kn.
Différences entre l’arbre B et l’arbre B+

Voici les différences entre l’arbre B et l’arbre B+ :
| Arbre B | Arbre B+ |
|---|---|
| Dans l'arborescence B, toutes les clés et enregistrements sont stockés dans les nœuds internes et feuilles. | Dans l'arborescence B+, les clés sont les index stockés dans les nœuds internes et les enregistrements sont stockés dans les nœuds feuilles. |
| Dans l'arborescence B, les clés ne peuvent pas être stockées de manière répétée, ce qui signifie qu'il n'y a pas de duplication de clés ou d'enregistrements. | Dans l'arborescence B+, il peut y avoir une redondance dans l'occurrence des clés. Dans ce cas, les enregistrements sont stockés dans les nœuds feuilles, tandis que les clés sont stockées dans les nœuds internes, des clés redondantes peuvent donc être présentes dans les nœuds internes. |
| Dans le Btree, les nœuds feuilles ne sont pas liés les uns aux autres. | Dans l'arborescence B+, les nœuds feuilles sont liés les uns aux autres pour fournir l'accès séquentiel. |
| Dans Btree, la recherche n'est pas très efficace car les enregistrements sont stockés dans des nœuds feuilles ou internes. | Dans l'arborescence B+, la recherche est très efficace ou plus rapide car tous les enregistrements sont stockés dans les nœuds feuilles. |
| La suppression des nœuds internes est un processus très lent et fastidieux car nous devons également prendre en compte l'enfant de la clé supprimée. | La suppression dans l'arborescence B+ est très rapide car tous les enregistrements sont stockés dans les nœuds feuilles donc nous n'avons pas à considérer l'enfant du nœud. |
| Dans Btree, l'accès séquentiel n'est pas possible. | Dans l'arborescence B+, tous les nœuds feuilles sont connectés les uns aux autres via un pointeur, un accès séquentiel est donc possible. |
| Dans Btree, plus le nombre d'opérations de fractionnement est effectué, ce qui entraîne une augmentation de la hauteur par rapport à la largeur, | L’arbre B+ a plus de largeur que de hauteur. |
| Dans Btree, chaque nœud a au moins deux branches et chaque nœud contient des enregistrements, nous n'avons donc pas besoin de parcourir les nœuds feuilles pour obtenir les données. | Dans l'arborescence B+, les nœuds internes ne contiennent que des pointeurs et les nœuds feuilles contiennent des enregistrements. Tous les nœuds feuilles sont au même niveau, nous devons donc parcourir jusqu'aux nœuds feuilles pour obtenir les données. |
| Le nœud racine contient au moins 2 à m enfants où m est l'ordre de l'arbre. | Le nœud racine contient au moins 2 à m enfants où m est l'ordre de l'arbre. |
