Un prisme est une figure solide tridimensionnelle comportant deux extrémités identiques. Il est constitué de côtés plats, de bases similaires et de sections égales. Ses faces sont des parallélogrammes ou des rectangles sans bases. Un tel prisme comportant trois faces rectangulaires et deux bases triangulaires parallèles est appelé prisme triangulaire. Les bases triangulaires sont reliées par des faces latérales parallèles les unes aux autres.
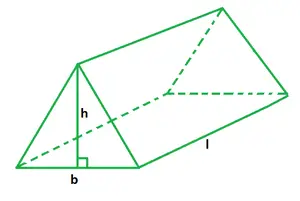
Volume d'une formule de prisme triangulaire
Le volume d’un prisme triangulaire est défini comme l’espace à l’intérieur ou l’espace rempli par celui-ci. Connaître l'aire de base et la hauteur d'un prisme triangulaire suffit pour calculer son volume. Le volume d’un prisme triangulaire est égal au produit de l’aire de la base et de la hauteur du prisme, également appelée longueur du prisme. L'aire de la base d'un prisme triangulaire est égale à la moitié du produit de la base triangulaire par son altitude.
Formule
V = (1/2) × b × h × l
où,
b est la base triangulaire,
h est l'altitude du prisme,
l est la longueur du prisme.
Exemples de problèmes
Problème 1. Trouvez le volume d'un prisme triangulaire si sa base mesure 6 cm, son altitude est 8 cm et sa longueur est 12 cm.
Solution:
Nous avons b = 6, h = 8 et l = 12.
impression javascriptEn utilisant la formule que nous avons,
V = (1/2) × b × h × l
= (1/2) × 6 × 8 × 12
= 3 × 8 × 12
= 288 cu. cm
Problème 2. Trouvez le volume d'un prisme triangulaire si sa base mesure 5 cm, son altitude est 7 cm et sa longueur est 8 cm.
Solution:
commande sed
Nous avons b = 5, h = 7 et l = 8.
En utilisant la formule que nous avons,
V = (1/2) × b × h × l
= (1/2) × 5 × 7 × 8
= 5 × 7 × 4
= 140 cu. cm
Problème 3. Trouvez la longueur du prisme triangulaire si sa base est de 6 cm, son altitude est de 9 cm et son volume est de 98 cu. cm.
Solution:
Nous avons b = 6, h = 9 et V = 98.
En utilisant la formule que nous avons,
V = (1/2) × b × h × l
=> 98 = (1/2) × 6 × 9 × l
haricot java=> 196 = 27l
=> l = 196/27
=> l = 7,25 cm
Problème 4. Trouvez l'altitude du prisme triangulaire si sa base est de 8 cm, sa longueur est de 14 cm et son volume est de 504 cu. cm.
Solution:
Nous avons b = 8, l = 14 et V = 504.
En utilisant la formule que nous avons,
V = (1/2) × b × h × l
=> 504 = (1/2) × 8 × h × 14
=> 504 = 56h
=> h = 504/56
L'algorithme de 'prim'=> h = 9 cm
Problème 5. Trouvez l'aire de la base du prisme triangulaire si sa longueur est de 18 cm, sa hauteur est de 10 cm et son volume est de 450 mètres cubes. cm.
Solution:
Nous avons l = 18, h = 10 et V = 450.
En utilisant la formule du volume que nous avons,
V = (1/2) × b × h × l
=> 450 = (1/2) × b × 10 × 18
=> 450 = 90b
=> b = 450/90
=> b = 5 cm
Par conséquent, l’aire de la base triangulaire est :
A = (1/2) × b × h
= (1/2) × 5 × 10
= 25 cm²
