Volume d'une sphère est la quantité de liquide qu’une sphère peut contenir. La formule du volume de la sphère est donnée par 4/3πr³. C'est l'espace occupé par une sphère dans un espace tridimensionnel. Il est mesuré en unité³c'est-à-dire m³, cm³, etc. Une sphère est un objet solide tridimensionnel de forme ronde en géométrie.

Le volume de la sphère est l'espace total occupé par la surface de la sphère et il est proportionnel au cube du rayon de la sphère. Dans cet article, nous découvrirons en détail le volume de sphère, la formule de volume de sphère, les exemples de formule de volume de sphère et d'autres.

• Qu'est-ce que le volume d'une sphère ?
• Formule du volume de la sphère
• Volume d'une sphère solide
• Volume d'une sphère creuse
• Volume de dérivation de formule de sphère
• Comment calculer le volume d'une sphère ?

Qu'est-ce que le volume d'une sphère ?

Le volume d’une sphère est la quantité d’espace qu’elle occupe à l’intérieur. La sphère est une forme solide ronde tridimensionnelle dans laquelle tous les points de sa surface sont également espacés de son centre. La distance fixe est le rayon de la sphère et le point fixe est le centre de la sphère. Nous remarquerons un changement de forme lorsque le cercle sera tourné. La rotation de l’objet bidimensionnel appelé cercle donne la forme tridimensionnelle d’une sphère.

Apprendre encore plus,

• Sphère
• Surface de la sphère

Définition du volume d'une sphère

Le volume d'une sphère est la masse totale entourée par la surface de la sphère. C'est l'espace 3D à l'intérieur de la sphère. Cela dépend du rayon de la sphère. L'image ajoutée ci-dessous montre une sphère de rayon r et son volume.

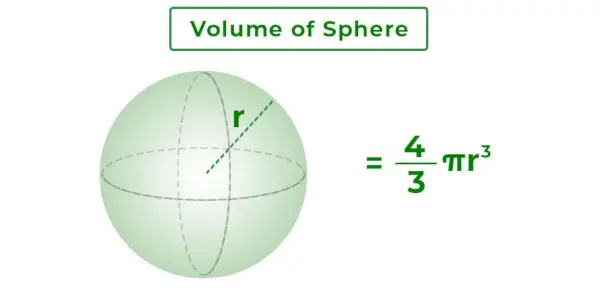
Formule du volume de la sphère

La formule du volume de la sphère est la formule utilisée pour trouver le volume de la sphère lorsque son rayon est donné. La formule du volume de sphère pour la sphère de rayon R est ajoutée ci-dessous,

Formule du volume de la sphère = 4/3πr ³

Où,

• r est le rayon d'une sphère
• Pi est une constante et sa valeur est 22/7

Une sphère est généralement classée en deux qui sont :

• Volume de la sphère solide
• Volume de la sphère creuse

Apprenons-les en détail.

Volume d'une sphère solide

Une sphère solide est une sphère entièrement remplie jusqu’à l’intérieur. c'est-à-dire qu'il a une masse jusqu'à son noyau et sa formule pour le volume lorsque son rayon est r est,

Volume d'une sphère solide (V) = (4/3)πr ³

Volume d'une sphère creuse

Pour une sphère creuse, son espace interne est vide et supposons que son rayon extérieur soit R. et son rayon intérieur est r, alors son volume est calculé à l'aide de la formule,

Volume de la sphère creuse = (4/3)π(R ³ – r ³ )

Volume de dérivation de formule de sphère

La formule du volume de la sphère peut être dérivée en utilisant les méthodes suivantes :

• Utiliser l'intégration
• Utilisation de la relation d'Archimède entre cylindre, cône et sphère

Discutons de ces méthodes en détail comme suit :

Volume de sphère utilisant l'intégration

En utilisant l’approche d’intégration, nous pouvons simplement calculer le volume d’une sphère.

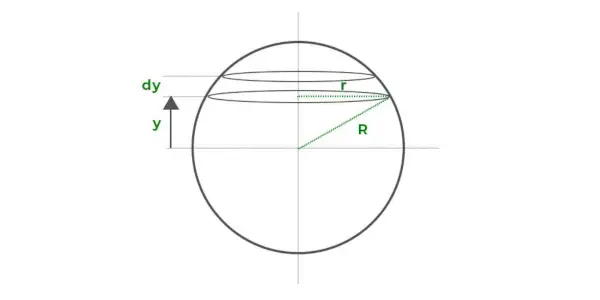
Supposons que le volume de la sphère soit constitué d’une série de minces disques circulaires empilés les uns sur les autres, comme illustré dans le diagramme ci-dessus. Chaque disque mince a un rayon de r et une épaisseur de dy qui est à une distance de y de l'axe des x.

Soit le volume d'un disque dV. La valeur de dV est donnée par,

dV = (πr²) toi

Ainsi, dV = π (R²- et²) toi

Le volume total de la sphère sera la somme des volumes de tous ces petits disques. La valeur requise peut être obtenue en intégrant l'expression de la limite -R à R.

Ainsi, le volume de la sphère devient :

V =int_{y=-R}^{y=R} dV

⇒ V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V =pi left[2R^3-frac{2R^3}{3} ight]

⇒ V =frac{4}{3}pi R^3

Ainsi, la formule du volume de la sphère est dérivée.

Volume de la sphère utilisant les relations d'Archimède

Comme Archimède l'a déjà prouvé, si un cône, une sphère et un cylindre ont le même rayon r et la même hauteur, leurs volumes sont dans le rapport de 1:2:3.

On peut donc dire :

Volume du cylindre = Volume du cône + Volume de la sphère

Ainsi, Volume de la sphère = Volume du cylindre – Volume du cône

Comme nous le savons, ce volume du cylindre = πr²h et volume du cône = (1/3)πr²h

En substituant ces valeurs dans l'équation, nous obtenons :

Volume de la sphère = πr²h – (1/3)πr²h = (2/3)πr²h

Nous supposons que la hauteur du cylindre est égale au diamètre de la sphère, qui est 2r. Ainsi:

Le volume de la sphère est (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Vérifiez également

• Formule de volume de calotte sphérique
• Formule de secteur sphérique
• Formule de segment sphérique

Comment calculer le volume d'une sphère ?

Le volume d'une sphère est l'espace occupé par une sphère. Son volume peut être calculé à l'aide de la formule V = 4/3πr ³ .

Les étapes nécessaires pour calculer le volume d’une sphère sont :

Étape 1: Marquez la valeur du rayon de la sphère.

2 septembre : Trouvez le cube du rayon.

Étape 3: Multipliez le cube du rayon par (4/3)π

Étape 4: Ajouter le (unité)³à la réponse finale.

Exemple pour calculer le volume d'une sphère

Exemple : Trouvez le volume d'une sphère d'un rayon de 7 cm.

Étant donné, r = 7 cm

V = (4/3)πr³

Volume de la sphère, V = ((4/3) × π × 7³) cm³

Hauteur = 1436,8 cm³

Le volume de la sphère est donc de 1436,8 cm³

En savoir plus

• Volume du cône
• Volume du cube
• Volume du cylindre

Exemples de volume de sphère

Exemple 1. Trouvez le volume de la sphère dont le rayon est de 9 cm.

Solution:

On a, r = 9

Volume de la sphère = 4/3 πr³

⇒ Volume de la sphère = (4/3) (3,14) (9) (9) (9)

⇒ Volume de la sphère = (4) (3,14) (3) (9) (9)

⇒ Volume de la sphère = 3052 cm³

Exemple 2. Trouvez le volume de la sphère dont le rayon est de 12 cm.

Solution:

On a, r = 12

Volume de la sphère = 4/3 πr³

⇒ Volume de la sphère = (4/3) (3,14) (12) (12) (12)

⇒ Volume de la sphère = (4) (3,14) (4) (12) (12)

⇒ Volume de la sphère = 7234,56 cm³

Exemple 3. Trouvez le volume de la sphère dont le rayon est de 6 cm.

Solution:

On a, r = 6

Volume de la sphère = 4/3 πr³

⇒ Volume de la sphère = (4/3) (3,14) (6) (6) (6)

⇒ Volume de la sphère = (4) (3,14) (2) (6) (6)

⇒ Volume de la sphère = 904,32 cm³

Exemple 4. Trouvez le volume de la sphère dont le rayon est de 4 cm.

Solution:

On a, r = 4

Volume de la sphère = 4/3 πr3

⇒ Volume de la sphère = (4/3) (3,14) (4) (4) (4)

⇒ Volume de la sphère = (1,33) (3,14) (4) (4) (4)

⇒ Volume de la sphère = 267,27 cm³

Exemple 5. Trouvez le volume de la sphère dont le diamètre est de 10 cm.

Solution:

On a, 2r = 10

qu'est-ce que $home Linux

⇒ r = 5

Volume de la sphère = 4/3 πr³

⇒ Volume de la sphère = (4/3) (3,14) (5) (5) (5)

⇒ Volume de la sphère = (1,33) (3,14) (5) (5) (5)

⇒ Volume de la sphère = 522,025 cm³

Exemple 6. Trouvez le volume de la sphère dont le diamètre est de 16 cm.

Solution:

Nous avons, 2r = 16

⇒ r = 8

Volume de la sphère = 4/3 πr³

⇒ Volume de la sphère = (4/3) (3,14) (8) (8) (8)

⇒ Volume de la sphère = (1,33) (3,14) (8) (8) (8)

⇒ Volume de la sphère = 2138,21 cm³

Exemple 7. Trouvez le volume de la sphère dont le diamètre est de 14 cm.

Solution:

Nous avons, 2r = 14

⇒ r = 7

Volume de la sphère = 4/3 πr³

⇒ Volume de la sphère = (4/3) (3,14) (7) (7) (7)

⇒ Volume de la sphère = (1,33) (3,14) (7) (7) (7)

⇒ Volume de la sphère = 1432,43 cm³

Volume des questions pratiques Sphère

T1 : Trouvez le volume de la sphère dont le diamètre est de 34 cm.

T2 : Trouvez le volume de la sphère creuse dont le rayon intérieur est de 4 cm et le rayon extérieur est de 8 cm.

T3 : Trouvez le volume de la sphère dont le rayon est de 14 cm.

T4 : Quel est le volume d'une sphère dont le rayon est égal au côté d'un carré d'aire 144 m².

Volume de FAQ Sphère

Qu'est-ce que le volume de la sphère ?

Le volume de la sphère est l'espace occupé par la surface de la sphère.

Quelle est la surface d’une formule de sphère ?

La surface totale de la sphère de rayon r est, Superficie = 4πr ²

Quelle est la formule du volume d’une sphère ?

Le volume d'une sphère de rayon r est, Volume = 4/3πr ³

Comment trouve-t-on le volume de l’hémisphère ?

Le volume d'un hémisphère de rayon r est, Volume = 2/3πr ³

Quel est le rapport entre le volume de la sphère et celui de l'hémisphère ?

Si une sphère et un hémisphère ont le même rayon alors le rapport de leur volume est :

DANS ₁ : DANS ₂ = (4/3πr ³ ) : (2/3πr ³ ) = 2 : 1

Quelle est l’unité de volume d’une sphère ?

Le volume de la sphère est mesuré en m³, cm³, litres, etc. m ³ est l’unité de mesure standard.

Quel est le volume de la sphère lorsque son rayon est réduit de moitié ?

Volume de la sphère = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Volume/8. Le volume de la sphère devient donc un huitième.